В данной работе на основе закона сохранения энергии и решения соответствующего интегрального уравнения получено точное выражение для потенциальной энергии частицы по заданной зависимости периода финитного движения частицы от ее полной механической энергии, взятой в линейном приближении. Также проведено сравнение результата с известной потенциальной энергией в случае гармонических колебаний частицы.
Ключевые слова: одномерное финитное движение, зависимость периода от энергии, интегральное уравнение Абеля, гармонические колебания
Во многих теоретических и прикладных задачах классической механики [1], а также других разделов физики [2], включая теорию колебаний атомно-молекулярных систем, возникает необходимость определения зависимости периода или частоты колебаний от полной энергии той или иной частицы, совершающей подобное финитное движение в известном потенциальном поле. Однако нередко требуется знать решение обратной задачи — задачи о нахождении заранее неизвестной потенциальной энергии частицы, совершающей финитное движение в некотором — зачастую достаточно сложном — внешнем поле, по известной (либо из экспериментальных данных, либо из каких-либо иных теоретических предположений или оснований) зависимости периода или частоты такого движения от полной механической энергии частицы.
В общем виде для произвольной энергетической зависимости периода такая обратная задача не имеет готового решения, однако его можно получить в определенных частных случаях. В настоящей работе, на основе методики расчета, предложенной нами ранее в [3] в относительно простом случае, найдено точное решение более сложной задачи при нулевом и первом приближениях в разложении энергетической зависимости периода частицы в степенной ряд.
Рассмотрим частицу массой ![]() , которая может совершать финитное движение в симметричной потенциальной яме с потенциальной энергией
, которая может совершать финитное движение в симметричной потенциальной яме с потенциальной энергией ![]() и с полной механической энергией
и с полной механической энергией ![]() (
(![]() ). То есть будем предполагать, что
). То есть будем предполагать, что ![]() — монотонно возрастающая при
— монотонно возрастающая при ![]() функция, график которой симметричен относительно оси ординат, причем
функция, график которой симметричен относительно оси ординат, причем ![]() . Тогда, предполагая отсутствие диссипативных сил, в силу закона сохранения энергии будем иметь
. Тогда, предполагая отсутствие диссипативных сил, в силу закона сохранения энергии будем иметь
![]() .
.
Проинтегрируем это уравнение, разделяя переменные, в результате получим выражение, связывающее период финитного движения ![]() и потенциальную энергию
и потенциальную энергию ![]() частицы в виде
частицы в виде
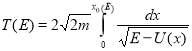 , (1)
, (1)
где ![]() — точка возврата, являющаяся корнем уравнения
— точка возврата, являющаяся корнем уравнения ![]() .
.
Перейдем под интегралом в (1) к новой переменной интегрирования
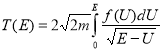 . (2)
. (2)
В таком виде выражение (2) представляет собой интегральное уравнение Абеля [4] относительно неизвестной функции ![]() , если считать, что
, если считать, что ![]() — заданная функция. Это означает, что если мы решим интегральное уравнение (2) и найдем функцию
— заданная функция. Это означает, что если мы решим интегральное уравнение (2) и найдем функцию ![]() , то затем найдем и искомую потенциальную энергию
, то затем найдем и искомую потенциальную энергию ![]() из решения задачи Коши для следующего дифференциального уравнения
из решения задачи Коши для следующего дифференциального уравнения
![]() . (3)
. (3)
Решение интегрального уравнения Абеля (2) как частного случая интегрального уравнения Вольтерра первого рода можно находить разными методами, однако проще его найти так, как описано в [4], в результате получим решение в следующем виде:
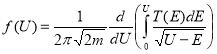 . (4)
. (4)
Далее будем считать, что известна степенная зависимость периода финитного движения частицы от ее полной энергии ![]() , которую представим в следующем виде
, которую представим в следующем виде
![]() , (5)
, (5)
где ![]() и
и ![]() — постоянные числа.
— постоянные числа.
Вычисляя интеграл в (4) с учетом (5) и затем дифференцируя по ![]() , получим функцию
, получим функцию ![]() в следующем виде
в следующем виде
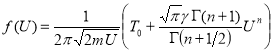 , (6)
, (6)
где
Наконец, подставляя найденную функцию ![]() в дифференциальное уравнение (3) и решая его при указанном начальном условии, приходим к следующему уравнению относительно неизвестной потенциальной энергии частицы:
в дифференциальное уравнение (3) и решая его при указанном начальном условии, приходим к следующему уравнению относительно неизвестной потенциальной энергии частицы:
![]() , (7)
, (7)
где для краткости введены следующие обозначения:
![]() ,
, 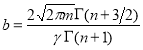 .
.
Очевидно, что для любого возможного ![]() уравнение (7) не имеет решения в явном виде. Анализ этого уравнения показал, что можно найти точное решение только в некоторых частных случаях, например, при
уравнение (7) не имеет решения в явном виде. Анализ этого уравнения показал, что можно найти точное решение только в некоторых частных случаях, например, при ![]() . Мы далее рассмотрим его решение при
. Мы далее рассмотрим его решение при ![]() , таким образом, будем искать потенциальную энергию частицы при заданной зависимости периода финитного движения частицы от ее полной энергии в линейном приближении:
, таким образом, будем искать потенциальную энергию частицы при заданной зависимости периода финитного движения частицы от ее полной энергии в линейном приближении:
![]() . (8)
. (8)
В результате при ![]() придем к кубическому уравнению канонического вида
придем к кубическому уравнению канонического вида
![]() ,
,
где для удобства введена новая переменная ![]() .
.
Воспользовавшись формулой Кардано [6] для решения подобных уравнений, в результате получим точное вещественное решение для потенциальной энергии частицы при известной линейной зависимости периода ее движения от полной энергии в виде
где для краткости введены следующие обозначения:
![]() ,
, 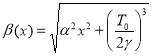 .
.
Легко проверить, что функция (9) является возрастающей при ![]() и удовлетворяет условию
и удовлетворяет условию ![]() .
.
Отметим также, что в нулевом приближении ![]() , т. е. когда период финитного движения частицы не зависит от ее энергии, из формулы (6) следует более простое выражение для функции
, т. е. когда период финитного движения частицы не зависит от ее энергии, из формулы (6) следует более простое выражение для функции ![]() :
:
![]() .
.
Тогда решая задачу Коши (3) с найденной функцией ![]() , в этом случае получим потенциальную энергию частицы в виде
, в этом случае получим потенциальную энергию частицы в виде
![]() , (10)
, (10)
где
![]() .
.
Таким образом, получили известный вид потенциальной энергии частицы в случае ее гармонических колебаний с периодом ![]() , при которых он, как известно, не зависит от энергии частицы [7]. При этом
, при которых он, как известно, не зависит от энергии частицы [7]. При этом ![]() имеет смысл коэффициента квазиупругой силы, действующей на частицу.
имеет смысл коэффициента квазиупругой силы, действующей на частицу.
Тот же результат (10) можно получить и из формулы (9) при условии малых отклонений частицы от положения устойчивого равновесия, т. е. при разложении полученной зависимости потенциальной энергии (9) в ряд при малых
В заключение заметим, что учет квадратичного члена, наряду с линейным, в разложении энергетической зависимости периода движения частицы (8) приводит к алгебраическому уравнению пятой степени, которое, согласно теореме Абеля [6], уже неразрешимо явно в радикалах, поэтому решение поставленной задачи в таком случае возможно лишь численными методами.
Литература:
1. Кузнецов А. П., Кузнецов С. П., Рыскин Н. М. Нелинейные колебания. — М., 2002. — 292 с.
2. Заславский Г. М., Сагдеев Р. З. Введение в нелинейную физику. От маятника до турбулентности и хаоса. — М., 1988. — 368 с.
3. Кочкин С. А., Розевика А. А. Задача о нахождении потенциальной энергии классической частицы по известной степенной зависимости периода ее финитного движения от полной энергии // Актуальные проблемы гуманитарных и естественных наук. — 2016. — № 8(1). — С. 23–26.
4. Краснов М. Л., Киселев А. И., Макаренко Г. И. Интегральные уравнения. Задачи и примеры с подробными решениями. — М., 2016. — 192 с.
5. Абрамовиц М., Стиган И. Справочник по специальным функциям. — М., 1979. — 832 с.
6. Алексеев В. Б. Теорема Абеля в задачах и решениях. — М., 2001. — 192 с.
7. Сивухин Д. В. Общий курс физики. Т. 1. Механика. — М., 2005. — 560 с.







