Основной целью образования становится не просто подготовка высокопрофессионального специалиста в той или иной области, но человека культуры, способного и готового к мирному плодотворному сосуществованию в обществе культурного плюрализма, основанном на гуманистических и демократических ценностях.
Главенствующую роль в современном образовании приобретает ориентация на развитие личности и профессиональной культуры, позволяющая облегчить процесс адаптации в профессиональной среде. Это требует оптимизации образовательной парадигмы профессиональной подготовки специалиста с учетом образовательного пространства [3, с.48].
Для определенных условий будущей деятельности специалиста оптимальным может оказаться изучение некоторых предметов на «ученическом» уровне, тогда как для других целью обучения может быть эвристическая и даже творческая деятельность [1]. Поэтому достижение цели возможно, если будет определен и достигнут необходимый уровень усвоения, а цель изучения математики в аграрных вузах состоит в том, что студент решает самостоятельно профессиональные задачи, определенные в модели специалиста и использующие математические методы, производя по памяти изученные алгоритмы. Тогда как под уровнем усвоения мы понимаем способность студента выполнять некоторые целенаправленные действия для решения определенного класса задач.
Понятие «задача» состоит из трех взаимосвязанных компонентов: цель, ситуация, деятельность. По способу использования усвоенной информации в решении задач можно различать два вида деятельности: репродуктивную и продуктивную. При репродуктивной деятельности усвоенные алгоритмы воспроизводятся в различных сочетаниях — от буквальной копии до некоторого свободного воспроизведения в типовых ситуациях. Для репродуктивной деятельности характерны в основном алгоритмические действия или действия по точно описанным правилам. К продуктивной относится эвристическая и творческая деятельность обучающихся.
Структуру деятельности по решению задач математическими методами мы обобщенно представили в виде следующих уровней:
1-й уровень — алгоритмическая деятельность при внешне заданном алгоритме (с «подсказкой») — «ученический» уровень;
2-й уровень — алгоритмическая деятельность по памяти (без «подсказки»);
3-й уровень — применение известных алгоритмов на неизвестных объектах — эвристическая деятельность;
4-й уровень — творческая, исследовательская деятельность — действия по неизвестным ранее алгоритмам.
Причем каждый последующий уровень сложнее предыдущего и включает его.
Определение необходимого уровня освоения математики требует уточнения понятий: алгоритм, эвристическая и творческая деятельность.
Алгоритм — способ решения вычислительных и других задач, точно предписывающий, как и в какой последовательности получить результат, однозначно определяемый исходными данными.
Из математических алгоритмов, изучаемых в вузах аграрного профиля, можно выделить следующие:
– вычисление определителей 2-го и 3-го порядка;
– нахождение произведения матриц;
– получение обратной матрицы с помощью алгебраических дополнений, элементарных преобразований;
– решение систем алгебраических уравнений методами: Крамера, Гаусса, с помощью обратной матрицы;
– нахождение производных сложных функций;
– различные методы интегрирования (метод замены переменных, интегрирование по частям, метод неопределенных коэффициентов и др.)
– нахождение экстремума функции 2-х переменных;
– нахождение наибольшего и наименьшего значения функции 2-х переменных;
– нахождение условного экстремума функции 2-х переменных методом Лагранжа;
– решение линейных дифференциальных уравнений 1-го порядка;
– решение однородных, неоднородных дифференциальных уравнений 2-го порядка с постоянными коэффициентами;
– нахождение вероятностей наступления событий;
– составление эмпирических функций распределения выборок;
– вычисление выборочной дисперсии;
– нахождение доверительного интервала;
– проверку статистических гипотез;
– метод наименьших квадратов;
– нахождение коэффициента корреляции;
– нахождение линейной и нелинейной регрессионной зависимости и т. д.
Решение абстрактных задач при внешне заданном алгоритме и алгоритмической деятельности по памяти соответственно были отнесены к 1-му и 2-му уровню усвоения, которые характеризуют репродуктивную деятельность обучающихся.
Наибольшие дискуссии вызывает понятие эвристическая деятельность. Ряд исследователей [2] под эвристической деятельностью понимают открывшийся объекту ранее не известный ему способ действия, способ решения. Нам близко мнение Я. А. Пономарева [2], определяющего эвристическую деятельность как специфические приемы, сформированные у обучающихся в ходе решения одних задач и сознательно перенесенные на другие задачи.
Анализ условий и процесса решения эвристических задач имеет ряд специфических черт:
– разветвленность процесса;
– отождествление некоторого искомого объекта с известным или вспомогательным неизвестным объектом;
– наличие стадии выдвижения стратегии решения;
– многовариантность путей решения [2].
Рассмотрим на примере следующую профессиональную задачу.
Задача. Определить, имеется ли взаимосвязь между жирностью молока и величиной жировых шариков, если 10 измерений этих параметров дали следующие результаты: жирность — 83, 72, 69, 90, 90, 95, 95, 91, 75, 70; величина жировых шариков — 56, 42, 18, 84, 56, 107, 90, 68, 31, 48.
Указанные измерения можно представить как выборочную совокупность, имеющую два признака xiи yi. Зависимость между этими признаками определяет коэффициент корреляции. Решая данную задачу с помощью отклонений от средних (Так как объем выборки небольшой (n=10)), мы получаем:
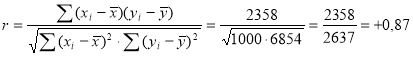
В данном случае коэффициент корреляции получается с положительным знаком, следовательно, между этими признаками существует зависимость.
В решении этой задачи мы видим такие черты эвристической деятельности как:
– отождествление жирности молока и величины жировых шариков со статистическим понятием выборочной совокупности и вариационным рядом, а зависимости между этими величинами с коэффициентом корреляции;
– наличие стадии выдвижения стратегии решения — в использовании статистических методов;
– многовариантность путей решения — в вычислении статистических показателей для данных, сгруппированных и несгруппированных в вариационные ряды.
Следовательно, профессиональные задачи, представленные в модели специалиста и использующие математические методы, можно отнести к эвристическим задачам, решение которых возможно на третьем уровне усвоения.
Под творческой деятельностью, соответствующей четвертому уровню освоения знаний, мы понимаем продуктивные действия, выполняемые путем самостоятельного конструирования новых правил, действий, алгоритмов, использование усвоенных знаний в нетипичных, нестандартных условиях.
Творческие, профессиональные задачи из модели специалиста, использующие математические методы вынесены на научно-исследовательскую работу (НИР) студентов. Тематика НИР на базе модели специалиста реализует главные принципы организации научно-исследовательской работы студентов. Она актуальна и связана с проблемами кафедр, с профессиональной деятельностью.
Профессиональные задачи, использующие наиболее часто повторяющие математические алгоритмы, нами вынесены как «базовые». Алгоритмы решения «базовых» профессиональных задач разбираются на практических занятиях и даются студентам для типовых расчетов.
В результате исследований произведено поуровневое структурирование комплекса учебных задач и учебно-профессиональных задач, которое представлено в таблице 1. Построенный нами комплекс учебных задач отвечает требованиям наличия ключевых связей, возрастания трудности на каждом уровне, целевой ориентации.
Таким образом, получаемые студентами экономические знания несут преимущественно абстрактный характер, недостаточно связаны с реальными проблемами, которые придется решать в будущей профессиональной деятельности.
Недостаточный уровень готовности студентов старших курсов к профессиональной деятельности во многом объясняется несформированностью представлений о профессии, излишней прагматичностью по отношению к учебной деятельности, преимущественной ориентацией на инструментальные знания, неразвитостью академической культуры.
Таблица 1
Поуровневое структурирование учебных иучебно-профессиональных задач (на примере дисциплин математического цикла)
|
№ |
Уровни усвоения |
Классификация задач |
Назначение |
Контрольные мероприятия |
|
1 |
2 |
3 |
4 |
5 |
|
1 |
0 |
Профессиональные задачи, не требующие знаний вузовского курса математики |
Демонстрация связи курса математики с профессией |
Текущий контроль |
|
2 |
1,2 |
Абстрактные задачи по готовым алгоритмам с «подсказкой» и «без подсказки» |
Овладение фундаментальными знаниями по математике |
Контроль по учебным темам |
|
3 |
2,3 |
«Базовые» профессиональные задачи |
Освоение готовых алгоритмов профессиональных задач на практических занятиях и в типовых расчетах |
Контроль по учебным модулям |
|
4 |
3 |
Эвристические профессиональные задачи |
Для индивидуальных занятий и самостоятельной работы студентов |
Семестровый контроль |
|
5 |
4 |
Творческие профессиональные задачи |
Проведение научно-исследовательской работы студентов |
Итоги студенческих, научных конференций |
Для достижения целостности подготовки, развития экономического мышления и поведения целесообразно вместо экстенсивного пути в отборе содержания отдавать предпочтение интенсивному пути, то есть ориентироваться не столько на полноту изучаемой дисциплины, сколько на интегративный, междисциплинарный подход, на изучение экономических проблем.
Успешность экономической подготовки зависит от эффективности экономического воспитания, повышения мотивации к учебно-профессиональной деятельности, применения специального комплекса мер по повышению профессиональной направленности.
Литература:
- Беспалько В. П., Беспалько Л. В. Педагогическая технология. Новые методы и средства обучения. — Вып. 2. — М.: Знание, 1989.
- Пономарев, Я. А. Психология творчества и педагогика / Я. А. Пономарев. — М., 2001
- Виноградова М. В., Якобюк Л. И. Основные тенденции развития высшего профессионального образования в контексте глобализации. // Агропродовольственная политика России. 2013.№ 11 (23). с. 48–50.







