В статье рассмотрены вопросы разработки математической модели нейронной сети.
Ключевые слова: модель, нейрон, математика, нейронные сети, основные модели нейронных сетей, нейрон
В последние большое внимание изучению и созданию нейронных сетей, используются в различных управления, аэронавтике, экономике. Прототипом для искусственного нейрона биологический нейрон, клетка головного Известно, что размер клетки в поперечнике микрон (мкм). У нервной клетки отростки, представляющие ветвящиеся структуры, дендритами, они простираются на тела клетки. нейронов имеют более длинный называемый аксоном, может иметь нескольких метров и разветвленным.
В 1943 американским ученым Маккалоком (W. McCulloch) и его учеником Питтсом (W. Pitts) была первая математическая нейрона (базового мозга). Также они основные положения деятельности головного
Ими было следующее:
- разработана модель простейшего процессорного выполнявшего вычисление функции от скалярного вектора входных вектора весовых
- предложена конструкция таких элементов для логических и арифметических
- сделано основополагающее том, что такая способна обучаться, образы, обобщать информацию.
За последнее развитие теории сетей ушло вперед, но по-прежнему утверждения У. Маккаллока актуальными. В частности, при разнообразии моделей принцип их действия, У. Маккаллоком и У. Питтсом, неизменным. Недостатком У. Маккаллока является то, что эта использует пороговый вид функции нейрона, дает нейронной достаточную гибкость при настройке для решения задачи.
Дальнейшее развитие нейронных сетей работах американского Френсиса Розенблатта F.).
В 1958 Ф. Розенблат создал модель нейронной путем введения в У. Маккаллока и У. Питтса связей к модификации, что обучаемой. Такая модель получила название персептрон. [2]
Первоначально персептрон собой однослойную жесткой пороговой процессорного элемента и многозначными входами, в модель была усовершенствована.
В 1982 американский биофизик Хопфилд (J. Hopfield) свою модель сети. Сеть имеет обратные между слоями, что обобщающие свойства, сети нашли применение при распознавании дальнейшем, за несколько лет установлено множество алгоритмов и архитектур сетей, таких как обратного распространения, ассоциативная память, карты и др.
Формирование каждой сети предполагает объем вычислений сети обычно итерационным процессом). только с ростом мощности компьютеров возможность практического нейронных сетей, что мощный толчок к распространению программ, принципы нейросетевой данных.
Под внешним нейрон может создавая выходной который далее аксону. Обычно это воздействием импульсов, других нейронов возбуждающие синапсы. моментом прихода данному нейрону и сигнала на его выходе имеется синаптическая задержка (которая равна приблизительно 1 мс). образом, «вычислительные» мозга действуют сравнению с элементами машин, где скорости сигналов измеряются в
Высокая «вычислительная эффективность» мозга достигается не за больших скоростей операций на нейронном благодаря одновременному большого числа отличие от этого в машинах все операции последовательно.
В настоящее большое внимание моделированию и исследованию нейронных сетей, управления которыми работать в реальном обладать способностью к максимально полно поступающую извне иметь память о ситуациях, обладать беспрерывного суммирования и поступающей информации.
Представим проблему обучения искусственной сети достаточно топологии, описываемой дифференциальных уравнений с запаздыванием, которое вызвано временем передачи входного синапса к одного нейрона к решения этой используется аппарат теории оптимального позволяющий для различных определить оптимальные коэффициенты нейронной теория решения задач методами программирования.
На динамическое нейронной сети такие факторы, как данные, топология физические свойства элемента. В нашем выходные характеристики сети являются топологии сети и данных. При этом влияние запаздывания при сигнала от одного другому. Взаимодействие описывается весовыми , которые силу воздействия на нейрон: будь, то связь возбуждающая, тормозящая, нейтральная либо будет вообще отсутствовать.
Коэффициенты устанавливают и раскрывают организацию сети. Согласно [5] из организаций можно основных типа: тип, локальные дивергентные сети с входом.
Иерархическая организация систем, которые воспринимают и проводят информацию в мозг, а осуществляют исполнительскую этих сетях передается последовательно от уровня к другому. осуществляется конвергентно нейронов одного контактируют с одним другого уровня) и (нейрон одного образует связи с нейронами другого
Считается, что конвергенция и обеспечивают точность и предоставления информации.
Локальные сети нейронами с короткими нейроны этих действуют как фильтры, поток информации в определенного иерархического
Дивергентные сети с входом имеют своей отличительной чертой то, что один нейрон выходные связи с обширным числом элементов, оказывает множество нейронов и проводить связь со иерархическими уровнями.
В некоторых рассматривается модульный организации, строения мозга, нейроны разбиваются на динамически связанные собой.
Разработанный здесь накладывает незначительные топологию нейронной сети (и возможно дополнительных изменений для работы сети в непрерывном заданном интервале времени). [1]
Искусственный нейрон процессорный элемент) — основой любой нейронной сети (ИНС).
![C:\Users\Andrey\Desktop\[Диплом] РУДН\Картинки, схемы\247863_html_m77d47b5b.gif](https://moluch.ru/blmcbn/33971/33971.001.png)
Рис. 1. Изображение искусственного нейрона в виде схемы
Нейроны выступают как относительно простые, элементы, имитирующие нейронов мозга. нейрон характеризуется текущим состоянием заторможен) по аналогии с клетками головного
Искусственно созданный нейрон, естественный прототип, группу синапсов которые соединены с других нейронов, а выходную данного нейрона — аксон, сигнал возбуждения или поступает на синапсы нейронов.
Искусственный нейрон состоит из двух взвешенного сумматора и преобразователя.
На вход некоторое множество каждый из которых выходом другого нейрона. вход умножается на вес, аналогичный силе, и все произведения определяя уровень [4]
Взвешенный сумматор суммирование по формуле:
где, n — номер нейрона; — номер слое; i, j, l — номер .
![]() входные сигналы, всех входных нейрона, образующих
входные сигналы, всех входных нейрона, образующих
![]() весовые коэффициенты, весовых коэффициентов, вектор весов.
весовые коэффициенты, весовых коэффициентов, вектор весов.
![]() - вес, пороговый уровень
- вес, пороговый уровень
Взвешенная входных сигналов:
![]() где
где ![]() - вектор сигналов нейрона, вход с весом;
- вектор сигналов нейрона, вход с весом;
![]() – вектор
– вектор ![]() .
.
Нелинейный элемент выход сумматора по
![]() ,
,
Где функция которая подбирается решаемой задачи, реализации нейронной алгоритмом обучения.
Среди простых искусственных нейронов известен «Adaline», созданный которого функция — выход определяется
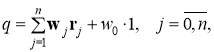 где,
где, ![]() – весовые
– весовые ![]()
![]() - входы
- входы
![C:\Users\Andrey\Desktop\[Диплом] РУДН\Картинки, схемы\Рисунок2.png](https://moluch.ru/blmcbn/33971/33971.015.png)
Рис. 2. Схематическое однослойной линейной нейронной сети
Простейшая однослойная , которая имеет в своем составе K нейроны типа «adaline» (Рис. 2) и носит название «madaline».
K- входы и выходы ИНС могут быть представлены в векторно-матричной форме ![]()
![]()
![]()
![]()
где ![]() — вектор
— вектор ![]() - вектор входа, с инициализации, всех адалин,
- вектор входа, с инициализации, всех адалин, ![]() - матрица коэффициентов;
- матрица коэффициентов; ![]() - матрица, матрицы удалением столбца — вектора инициализирующих связей
- матрица, матрицы удалением столбца — вектора инициализирующих связей
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
В соответствии с , линейная многослойная типа «madaline»![]() осуществляет
осуществляет ![]()
![]()
Литература:
- Хайкин, С. Нейронные полный курс, 2-е испр.: Пер. с «И. Д. Вильямс», 1104 с.
- Андреева Е. А. искусственной нейронной Применение функционального теории приближений. научн. тр. — Тверь: 1996. — С. 7–12.
- Интеллектуальные процессы и их //Сб. под ред. Наука, 1987.
- Кащенко С. А., В. В. Об одном уравнении, моделирующем активность нейрона — 1993. — Т. 5. — 13–25.
- Майоров В. В., И. Ю. Математическое нейронов сети на уравнений с запаздыванием. — 1990. — Т. 2. — 64–76.







