Комбинированный алгоритм линейной оптимизации с поиском максимального потока на графе



В данной статье приводится описание комбинированного алгоритма линейной оптимизации с поиском максимального потока на графе на примере оптимизации работы железнодорожной станции со сложной топологией путей.

Ключевые слова: максимальный поток, транспортная задача, целочисленное линейное программирование, задача нахождения минимального пути между вершинами графа

Планирование и контроль выполнения планов железнодорожных перевозок невозможны без анализа использования технических средств, учета и оценки их работы. Наибольшую сложность вызывают задачи в железнодорожных станциях, представляющих собой сложные многомерные системы: сложная топология путей, пустые и груженые вагоны, значительное количество входов и выходов, тупиков, депо, светофоров, стрелок, перекрестков и т. д. Одними из наиболее затратных составляющих организации эксплуатации станции являются задействование локомотивов с целью минимизации нахождения на ней грузов. Поэтому решение проблемы повышения эффективности эксплуатации станционного хозяйства является актуальной научной задачей, имеющей большое практическое значение.

Постановка задачи

Задана железнодорожная станция, состоящая из следующих компонент:

– Источники пустых вагонов (тупики, депо и пр.);

– Платформы с грузом, который нужно вывезти с ж/д станции;

– Выезды из станции, ведущие к потребителям;

– Топология станции (ж/д пути, стрелки, перекрестки, светофоры и пр.).

Поскольку эксплуатация локомотивов, обеспечивающих продвижение вагонов от одной компоненты станции к другой, является одной из наиболее затратных операций, в работе поставлена задача повышения эффективности использования бюджета времени локомотивного и среднесуточного пробега вагонного парков. Для этого необходимо решить следующие взаимоувязанные задачи оптимизации в рамках данной ж/д станции:

– Минимизировать бюджет времени использования локомотивов;

– Минимизировать среднесуточный пробег вагонов.

При решении этих задач необходимо учитывать количественные показатели функционирования станции, к которым относятся:

– объем перевозок (отправления) грузов;

– грузооборот;

– число вагонов или масса грузов, погруженных за сутки.

Работа вагонного парка определяется для всей сети числом вагонов, погруженных за сутки, а для дорог и отделений — суммой вагонов своей погрузки и принятых груженых вагонов от других дорог и отделений. Так как принятые вагоны могут быть или выгружены, или сданы гружеными, работа определяется как сумма выгруженных и сданных груженых вагонов.

Основными качественными показателями работы железных дорог и их подразделений являются:

– соблюдение графика движения, выполнение плана перевозок и плана формирования поездов;

– реализация технической, участковой и маршрутной скоростей движения поездов;

– степень использования подвижного состава, характеризующаяся:

1. оборотом;
2. бюджетом времени;
3. среднесуточным пробегом и производительностью локомотивов;
4. оборотом и среднесуточным пробегом вагонов;
5. статической и динамической нагрузкой;
6. производительностью грузовых вагонов.

Оборот локомотива определяется продолжительностью обслуживания им одной пары поездов на участке обращения, т. е. промежутком времени с момента выдачи локомотива под поезд до момента выдачи его под следующий поезд.

При работе локомотивов по удлиненным участкам обращения, выходящим за пределы границ отделения, а иногда и дороги, вводится дополнительный показатель использования локомотивов, называемый их бюджетом времени. Этот показатель характеризует расчленение, часы или %, времени работы на отдельные операции: движение на перегонах, простои на промежуточных станциях, нахождение на станциях смены бригад, в пунктах оборота и на станции приписки.

Комплексным показателем использования локомотива является его суточная производительность, тонно-километры (ткм) брутто/локомотив, определяемая делением общего грузооборота на участках обращения локомотивов за сутки на численность эксплуатируемого парка локомотивов, в состав которого входят локомотивы, находящиеся во всех видах движения, а также подвергаемые техническим операциям и осмотру.

Универсальным показателем качества работы железных дорог и использования подвижного состава, отражающим уровень организации труда всех работников железных дорог и подъездных путей предприятий, является оборот вагона, т. е. промежуток времени между двумя последовательными погрузками в один и тот же вагон.

Оборот вагона представляет собой сумму времени нахождения вагона в поездах на участках (в движении и на промежуточных станциях) и транзитного вагона — на технических станциях (в транзитных поездах и под переработкой), а также станциях погрузки и выгрузки. Оборот вагонов имеет большое значение для экономики в целом: им определяются не только качество использования подвижного состава и транспортные издержки, но и продолжительность перевозки грузов.

Описание решения проблемы

Учитывая ограничения реальной системы, разработанный программный комплекс формирует граф структуры ж/д станции и на его основе строит модель многоэтапной двухкритериальной оптимизации функционирования локомотивного и вагонного парков:

– На первом этапе производится минимизация максимального времени прохождения составом железнодорожной сети станции;

– На втором этапе строится оптимальный план распределения вагонов с целью минимизации их среднесуточного пробега.

1 этап: Минимизация бюджета времени локомотивов на ж/д станции

Для минимизации времени использования локомотивного парка необходимо произвести перераспределение весов ребер графа, т. е. максимально допустимых скоростей движения по конкретным участкам ж/д станции. Изначально максимально допустимые скорости движения задаются согласно реальным данным.

Пусть имеется взвешенный граф , где — множество вершин графа (узлов), а — множество дуг. Вершины графа соответствуют компонентам железнодорожной станции (см. Постановку задачи), а дуги, называемые так же ребрами, — участкам путей между этими компонентами, при этом вес ребра проассоциирован со временем, которое нужно потратить на прохождение данного участка пути. Для перераспределения весов ребер используется задача о максимальном потоке на сети, которая позволяет минимизировать максимальное время прохождения составом железнодорожной сети станции:

.

Для решения задачи необходимо преобразовать исходный граф в ориентированный граф (орграф). Для этого необходимо ввести дополнительные ребра, равные по весу уже существующим, но обратные по направлению. Стоит отметить, что нет необходимости вводить дополнительные ребра, если оригинальное ребро выходит из источника вагонов либо заканчивается на выезде со станции, так как в этих случаях направления путей определяются однозначно.

На следующем шаге водятся дополнительные узлы — «Исток» и «Сток». Первый узел соединяется со всеми источниками вагонов, из которых начинается движение системы, второй — с выездами из станции, которые являются конечными пунктами. Веса введенных ребер должны быть больше максимального веса уже существующего ребра, чтобы не оказывать влияние на систему в целом.

После этого решается известная задача о максимальном потоке любым известным способом (например, при помощи алгоритма Форда — Фалкерсона).

Минимизация времени прохождения графа производится за счет перераспределения ходовых скоростей (весовых коэффициентов) на его ребрах с учетом существующих ограничений.

Для перехода к следующему этапу полученный граф с перераспределенными весами ребер необходимо подготовить. Для этого нужно построить две матрицы распределения времени и, характеризующие минимальное время прохождения пути от источников пустых вагонов до платформ и от платформ до выездов со станции соответственно. Для этого используется алгоритм нахождения кратчайшего пути между вершинами графа (алгоритм Флойда — Уоршолла [6]), т. е. решается следующая задача:

где — вес каждого ребра, , при условии, что для всех и с начальной вершиной обхода и конечной выполняется следующее равенство [6, 7]:

.

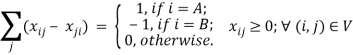2 этап: Минимизация среднесуточного пробега вагонов

После того, как были получены данные, соответствующие минимальному времени прохождения определенных участков путей ж/д станции, составляется план движения составов по этим путям, с учетом ограничений.

Пусть в системе имеется источников вагонов, каждый из которых может предоставить вагонов, , платформ, на каждой из них груза (груз здесь и далее измеряется в вагонах), , и выездов со станции, на каждый из которых нужно подать груза, . При этом подразумевается, что 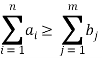, то есть количества пустых вагонов хватит на то, чтобы вывезти весь груз с платформ, и 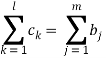, другими словами, на выезды со станции нужно подать столько же груза, сколько находится на платформах, излишек на станции не остается. Так же уже известны матрицы распределения времени и, полученные после первого этапа оптимизации. Тогда задача оптимизации среднесуточного пробега вагонов может быть разбита на две подзадачи:

1) Нахождение оптимального варианта подвоза пустых вагонов к платформам [1]:

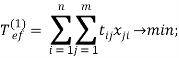
при следующих ограничениях:

;

;

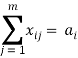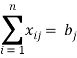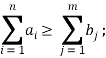
2) Оптимизация подачи загруженных вагонов к потребителям [1]:

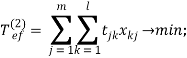
при следующих ограничениях:

;

;

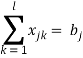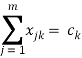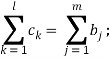
где и — планы распределения вагонов на участках от тупиков к платформам и от платформ к выездам со станции соответственно. Поставленная задача целочисленного программирования решается средствами MATLAB (OptimizationToolbox, функция целочисленного линейного программирования intlinprog, алгоритм поиска экстремума — interior-point-legacy). Результатом работы данного этапа являются оптимальные планы распределения вагонов — и , — и показатели эффективности работы системы и (размерность — вагоно-часы).

Пример работы программного комплекса

В качестве примера была взята схема станции «Рудная». Построенный на ее основе граф содержит 237 ребер и 198 узлов, из них:

– 33 источника вагонов;

– 139 стрелок;

– 17 платформ;

– 9 выездов со станции.

Допустимый интервал ходовой скорости — [10; 40]. Результат визуализации данного графа представлен на Рис. 1.

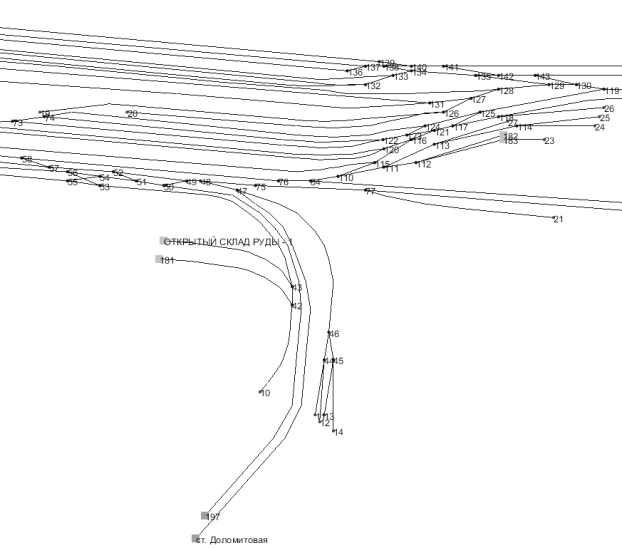
Рис. 1. Демонстрация работы визуализации введенных данных (фрагмент)

Для оценки качества работы программного комплекса, был задан пример распределения пустых вагонов по платформам и груженых вагонов по выездам из станции. В соответствии с ним суммарное время системы составило 2,11 часа, общая эффективность системы — 126,29 вагоно-часов.

По завершении работы программного комплекса были получены следующие итоговые показатели (для удобства исходные и полученные данные сгруппированы в таблицу см. Рисунок 2):

– Суммарное время системы — 1,49 часа;

– Общая эффективность системы — 86,79 часа.

Рис. 2. Результаты оптимизации

Так же программным комплексом были построены оптимальные планы распределения вагонов, представленные на Рисунок 3, Рисунок 4.

Время, потраченное на расчёты, составило 3,68 секунды.

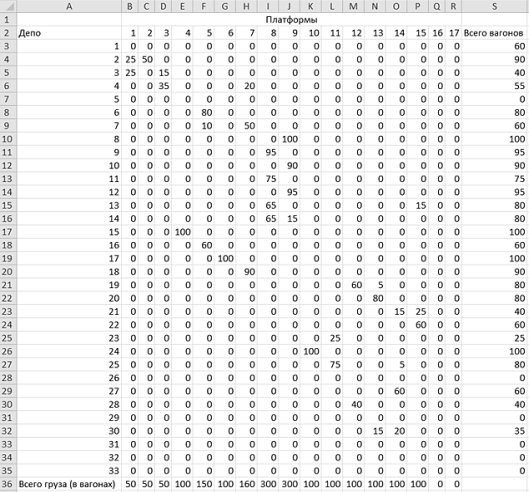
Рис. 3. Оптимальный план развоза пустых вагонов по платформам на погрузку

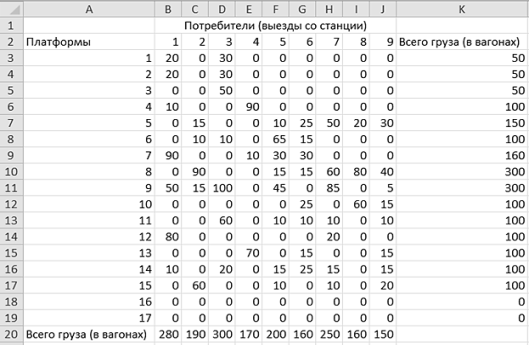
Рис.4. Оптимальный план подачи груза на выходы с платформ

Заключение

Разработанный алгоритм и построенный на его основе программный комплекс позволил решить задачу оптимизации использования локомотивного и вагонного парков станции со сложной топологией путей. Его использование позволило:

1. Снизить начальный бюджет времени (в приведенном примере показатель снижения составил 29,3 %);
2. Минимизировать среднесуточный пробег вагонов, повышая тем самым эффективность работы (в примере показатель роста — 31.1 %).

Метод поиска оптимального плана отличается своим быстродействием от использования классических методов оптимизации (по оценкам в 1.5–2 раза), что важно в применении данного алгоритма на практике. Разработанный программный комплекс также отлично справляется с «проклятием размерности» — в приведенном примере матрица транспортной задачи имела размерность 200 x 200.

Литература:

1. «Математические модели и методы в логистике»: учеб. пособ. / В. С. Лубенцова. Под редакцией В. П. Радченко. — Самара. Самар. гос. техн. ун-т, 2008, — 157с.
2. «Total time minimizing transportation problem» — Ilija Nicolic — Yugoslav Journal of Operations Research, 17(2007), Number 1, 125–133
3. «A New Approach to the Maximum-Flow Problem» — Andrew V.Goldberg, Robert E.Tarjan — Journal of ACM (JACM) Volume 35 Issue 4, Oct.1998, Pages 921–940
4. «Разрешимость транспортной задачи по критерию времени» — Е. И. Титова, А. В. Чапрасова — ж. «Молодой ученый». — 2014. — № 4. — С. 36–38
5. «Построение математических моделей в прикладных задачах» — Ю. А. Крымская, Е. И. Титова, С. Н. Ячинова — ж. «Молодой ученый». — 2013. — № 12(59). — С. 3–6
6. R. W. Floyd. Algorithm 97: Shortest path. Communication of the ACM 5(6):345, 1962.
7. Shortest Path URL: https://www.utdallas.edu/~chandra/documents/networks/net3.pdf(дата обращения: 21.09.2016)