В статье предложен алгоритм уплотнения структуры данных префиксного дерева, представленной в виде разреженной матрицы, которая используется при обработке информации методом лучевого поиска. Алгоритм позволяет уменьшить время, затрачиваемое на процесс уплотнения, за счет введения дополнительной процедуры учета статистических свойств битовой карты префиксного дерева.
Ключевые слова: поиск информации, автоматическая обработка текста, лучевой поиск, уплотнение структуры данных, префиксное дерево
В ходе решения ряда специфических задач по анализу и структурированию текстовой информации наиболее эффективным зарекомендовал себя алгоритм лучевого поиска (triesearch) [1]. В данном алгоритме, как правило, основная информационная структура хранится в виде префиксного дерева. Однако в ряде некоторых специальных задач обработки информации (например, фильтрация html-страниц по «черным» спискам доменных имен, URL) недостатком данного метода является большой объем памяти для хранения структуры префиксного дерева размером более 104 признаков вследствие сильной разреженности признаковой таблицы.
В этой связи возникает задача уплотнения префиксного дерева словаря признаков. Наиболее распространенный процесс уплотнения структуры данных рассмотрен в [1]. Он представляет собой попарное совмещение узлов (столбцов) таким образом, что ненулевые элементы не накладываются друг на друга. Процесс уплотнения таблицы префиксного дерева заключается в итерационном выборе (в случае аппроксимирующих алгоритмов — случайном итерационном выборе) двух столбцов матрицы состояний и переходов и проверке их на совместимость. В случае совместимости столбцов их совмещают (объединяют), получая в результате один столбец.
После уплотнения аппроксимирующим способом структура данных префиксного дерева занимает в порядки раз меньший объем оперативной памяти, нежели разреженный вариант. Это позволяет использовать данный способ уплотнения в современных информационных системах обработки информации. Однако, с другой стороны, уплотнение занимает значительное процессорное время. Так, например, уплотнение структуры данных префиксного дерева для 4·106 строк занимает 4–5 дней. Это связанно с тем, что при слиянии каждой пары узлов приходится производить проверку на пересечение двух битовых карт, что является ресурсоемкой операцией.
В общем случае, единственно применимым в условиях словарей больших объемов и требований ежедневного их обновления является поиск такой перестановки столбцов из всех возможных, при которой достигается наилучшее отношение количества занятых элементов к их общему количеству. Существует доказательство NP-полноты данного процесса [2]. Аппроксимирующие алгоритмы, основанные на принципе выбора первого найденного варианта [3] дают эффективный результат в случаях малой разветвленности узлов. В случаях, когда количество ключевых слов превышает 106, и при этом имеет место большая разветвленность, возникает задача разработки более эффективного алгоритма уплотнения. Данная задача может быть решена тем, что аппроксимирующий способ уплотнения структуры данных префиксного дерева будет дополнен тем, что слияние узлов будет происходить только после ранжирования и нахождения наиболее подходящих пар слияния. Таким образом, становится очевидной актуальность задачи разработки алгоритма уплотнения, учитывающего некоторые свойства и характеристики префиксного дерева и позволяющего ускорить процесс попарного совмещения столбцов при требуемом коэффициенте уплотнения.
Ввиду того, что на процесс уплотнения матрицы префиксного дерева влияет только наличие ненулевого элемента в той или иной ячейке, что в свою очередь можно представить поведением дискретной случайной величины — индикаторе заполненности ячейки. Таким образом, автором была выдвинута и подтверждена гипотеза: учет статистических характеристик индекса узлов префиксного дерева позволит построить более эффективную модель ее структуры с позиции уменьшения алгоритмической сложности процесса уплотнения при достаточном коэффициенте сжатия.
В ходе исследований, для сокращения времени уплотнения словаря признаков была разработана модель структуры данных префиксного дерева, учитывающая особенности ее построения и специфические признаки, которая обеспечила по результатам уплотнения в автоматическом режиме требуемое время работы алгоритма, максимизировав при этом степень уплотнения признаковой таблицы [4].
Результаты моделирования легли в основу предлагаемого алгоритма уплотнения структуры данных префиксного дерева, представленного на рисунке 1.
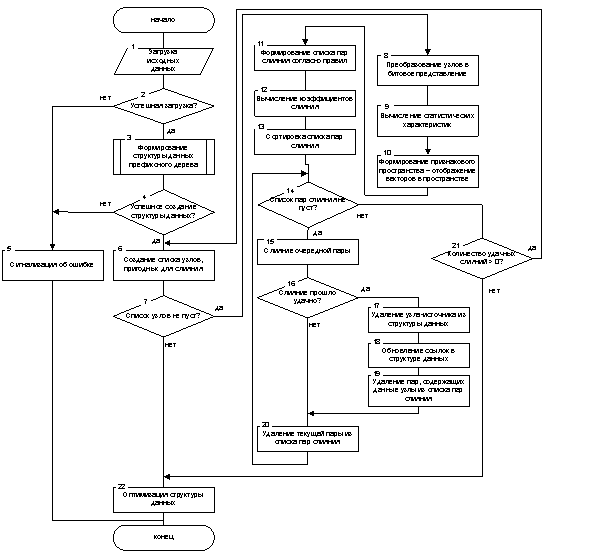
Рис. 1. Блок-схема алгоритма уплотнения структуры данных префиксного дерева
Определим показатели эффективности работы алгоритма уплотнения структуры данных префиксного дерева. Исходя из ограниченности вычислительных ресурсов, выделяемых на осуществление процедур уплотнения, очевидно, что помимо времени работы алгоритма, важна еще и степень уплотнения, которая выражается отношением количества занятых элементов префиксного дерева словаря признаков к их общему количеству (т. е. количества занятых ячеек к общему количеству ячеек признаковой таблицы):
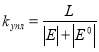 ,
,
где ![]() — коэффициент уплотнения,
— коэффициент уплотнения, ![]() — мощности множества значений элементов таблицы состояний и переходов и ее нулевых элементов соответственно. Максимального значения коэффициент уплотнения
— мощности множества значений элементов таблицы состояний и переходов и ее нулевых элементов соответственно. Максимального значения коэффициент уплотнения ![]() может достигнуть путем применения полного перебора возможных вариантов размещения признаков.
может достигнуть путем применения полного перебора возможных вариантов размещения признаков.
Исходные данные алгоритма:
Т — множество признаков;
К — мощность алфавита признаков;
L — количество узлов префиксного дерева;
Е — множество значений элементов таблицы состояний и переходов;
![]() — структура данных префиксного дерева словарных признаков (таблица состояний и переходов), содержащая занятые (ненулевые) элементы
— структура данных префиксного дерева словарных признаков (таблица состояний и переходов), содержащая занятые (ненулевые) элементы ![]() и свободные (нулевые) элементы
и свободные (нулевые) элементы ![]() ;
;
![]() — уплотненная структура данных префиксного дерева словарных признаков;
— уплотненная структура данных префиксного дерева словарных признаков;
![]() — время выполнения процесса уплотнения для аппроксимирующего алгоритма.
— время выполнения процесса уплотнения для аппроксимирующего алгоритма.
Результатом работы алгоритма является:
- Таблица элементов структуры данных префиксного дерева для словаря признаков W.
- Множество признаков статистических свойств элементов структуры данных и рациональных процедур их перестановки F(W) с целью уплотнения, основанное на статистической модели структуры данных.
- Уплотненная таблица структуры данных префиксного дерева, занимающая объем оперативной памяти при работе алгоритма лучевого поиска не более требуемого.
В итоге автором разработан алгоритм уплотнения словаря признаков отбора путем учета статистических свойств элементов префиксного дерева и применения рациональных процедур их перестановки, обеспечивающий минимизацию времени работы при достижении требуемого значения коэффициента уплотнения ![]() :
:
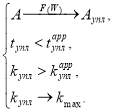
Проверка адекватности и оценка эффективности работы алгоритма производилась при следующих ограничениях:
объем набора ![]() признаков находился в пределах 105–107 признаков;
признаков находился в пределах 105–107 признаков;
размер алфавита ![]() ограничен размерностью 255 (1 байта информации) и постоянен в процессе уплотнения.
ограничен размерностью 255 (1 байта информации) и постоянен в процессе уплотнения.
Проведем оценку асимптотической сложности алгоритма. Предлагаемый алгоритм был дополнен процедурами вычисления статистических характеристик префиксного дерева и формирования признакового пространства (блоки 9 и 10, рис. 1). Данные процедуры линейно зависимы от количества узлов в битовой признаковой таблице, а коэффициент линейности будет определяться лишь количеством s вычисляемых статистических характеристик каждого столбца. Тогда, приняв O(f(N)) за асимптотическую сложность аппроксимирующего алгоритма уплотнения, можно определить сложность разработанного как — O(f(N) + sN). Однако учитывая, что наилучшие аппроксимирующие алгоритмы уплотнения имеют сложность близкую к субэкспоненциальной [3], то слагаемым sN можно пренебречь. С другой стороны, разделение узлов префиксного дерева на t классов слияния, переводит задачу перебора пар слияния к поиску этих пар внутри классов (сокращение мощности переборного множества), в добавок еще и со вспомогательным коэффициентом слияния kсл (блок 12, рис.1), уменьшая асимптотическую сложность алгоритма уплотнения в tkсл раз. Таким образом, представленный алгоритм уплотнения структуры данных префиксного дерева, учитывающий статистические свойства таблицы состояний и переходов, имеет сложность O(f(N)/tkсл).
Литература:
- Кнут, Д. Э. Искусство программирования. В 4 т. Т. 3. Сортировка и поиск: учебное пособие / Д. Э. Кнут. — 2-е изд.: пер. с англ. — Москва: Издательский дом «Вильямс», 2000. — 832 с.
- Dill, J. M. Optimal trie compaction is NP-complete. TR-CSD-167, Pennsylvania State Univ., March 1987.
- Марьянов, П. А. Сравнение реализаций алгоритмов цифрового поиска и конечных автоматов регулярных выражений / П. А. Марьянов, А. Л. Кузьмин // Телекоммуникации. — 2010. — № 11. С. 7–11.
- Марьянов, П. А. Статистическая модель структуры данных префиксного дерева на основе дискретного распределения / П. А. Марьянов // Телекоммуникации. — 2015. — № 3. С. 34–39.







