В период эксплуатации гидротехнические сооружения испытывают гидростатическое давление жидкости на плоские и криволинейные поверхности которое необходимо рассчитывать еще при проектировании сооружения.
При расчете гидротехнических сооружений необходимо знать силу давления жидкости на сооружение или его часть и точку ее приложения.
Для решения многих практических задач приходится строить эпюры гидростатического давления, представляющие собой графическое изображение распределения гидростатического давления на плоские прямоугольные поверхности.
Законы равновесия жидкости и их практическое применение рассматриваются в разделе гидравлики, называемом гидростатикой.
В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна. [1, с. 42-44]
Гидростатическое давление обладает следующими свойствами:
Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.
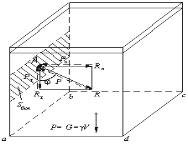
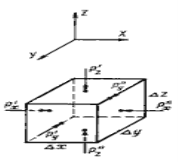
а)б)
Рис. 1. Схема, иллюстрирующая свойства гидростатического давления а – первое свойство; б - второе свойство
Свойство 2. Гидростатическое давление неизменно во всех направлениях.
![]()
Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.
![]()
Сила гидростатического давления жидкости на плоскую поверхность (стенку) определяется по формуле (расчетная схема представлена на рис.2)
![]() (1)
(1)
где P0 - давление на свободной поверхности жидкости;
hc- глубина погружения центра тяжести плоской фигуры;
![]() - площадь плоской фигуры.
- площадь плоской фигуры.
Если свободная поверхность жидкости находится под атмосферным давлением, формула (1) упрощается и принимает вид
![]() (2)
(2)
Точкой приложения силы гидростатического давления жидкости на плоскую фигуру является центр давления, который располагается ниже центра тяжести на величину эксцентриситета е.
Ордината центра давления уд определяется по выражению
![]() (3)
(3)
где ус – ордината центра тяжести плоской фигуры;
I- момент инерции плоской фигуры относительно горизонтальной оси, проходящей через центр тяжести.
Если плоская поверхность располагается вертикально, то ус = hc, yд=hд. Тогда
![]() (4)
(4)
В случае горизонтального расположения плоской поверхности центр тяжести и центр давления находятся в одной точке. [2, с. 36-40]
![]()
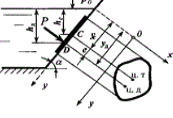
Рис. 2. Сила давления жидкости на плоскую поверхность (стенку)
Так как избыточное гидростатическое давление изменяется по линейному закону P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.
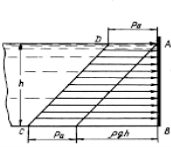
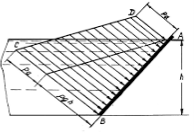
Рис.3. Эпюры абсолютного и избыточного давления жидкости на плоские поверхности
Полученные точки соединим прямой линией, В результате получим эпюру абсолютного гидростатического давления на плоскую стенку в виде трапеции. Пользуясь этой эпюрой можно графическим путём находить гидростатическое давление, соответствующее любой глубине жидкости.
Аналогично построим эпюру избыточного гидростатического давления. Избыточное давление на поверхности жидкости при l = 0 и h = 0 равно нулю. При l = L и h = Н избыточное давление равно Ризб. = glsin = gh. Соединяя полученные точки прямой линией, получим эпюру избыточного гидростатического давления на плоскую стенку в виде треугольника. Так как атмосферное давление распределяется равномерно по глубине, обычно, для упрощения расчетов пренебрегая Ра принимают эпюру гидростатического давления ГСД треугольной формы [3,с. 9].
При построении эпюры избыточного давления на плоские вертикальные и наклонные поверхности встречаются некоторые трудности.
![]()
![]()
![]()
![]()
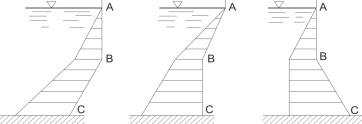
Рис 4. Некоторые случаи неверного выполнения графического изображения ГСД на плоские вертикальные и наклонные поверхности.
Для демонстрации эпюры избыточного давления жидкости на плоские вертикальные и наклонные поверхности нами предлагается использовать устройство, представленное на рисунке 5.
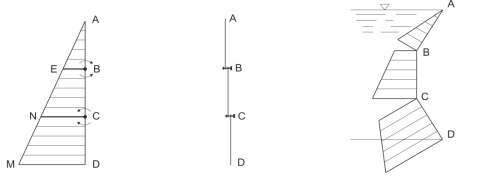
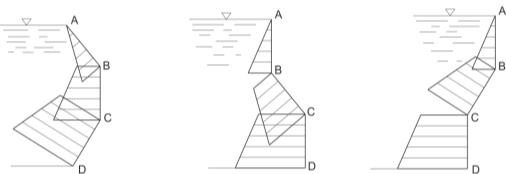
Рис 5. Демонстрация ГСД на плоские вертикальные и наклонные поверхности
Устройство в целом представляет собой прямоугольный треугольник АDM состоящий из нескольких фигур ABE, EBCN, NCDM свободно вращающихся вокруг осей В, С (фигуры вырезаны из прозрачного органического стекла). В данном случае высота треугольника АDM равняется сумме высот плоских поверхностей, испытывающих гидростатическое давление Hadm = Lавсд= Lав+ Lвс+ Lсд
При выполнении эпюры ГСД обычно допускают ошибки, не учитывая 1-ое свойство (Рис 4). В этом случае используя предлагаемое устройство можно быстро устранить ошибки. Приложив части фигур устройства на соответствующие плоскости можно получить эпюры ГСД. Используя это устройство можно с определенной легкостью и без ошибок построить эпюры на плоские вертикальные и наклонные поверхности (Рис. 5). Устройство позволит ускорить усвоение студентами отведенного материала на выполнение графического изображения ГСД на плоские вертикальные и наклонные поверхности.
Данное устройство не рекомендуется использовать при демонстрации эпюры на горизонтальные поверхности.
Литература:
- Штеренлихт Д.В. Гидравлика. - М.: Энергоатомиздат, 1984. – 640 c.
- Чугаев Р.Р. Гидравлика. – 4-е изд. – Л.: Энергоиздат, 1982. – 672 с.
- Гаврилов М.Б. Гидравлика, Алматы: ТОО «Издательство LEM»,2004. – 316c.







