Предлагаемая статья относится к области математической логики, моделирования, рассмотрены вопросы, относящиеся к физиологии головного мозга человека.
Как формируется мысль? Какова ее природа? Каким законам подчиняется процесс мышления? Эти вопросы нашего сознания до настоящего времени остаются малоизученными. Исследование процесса мышления только в рамках физиологии или психологии не позволяет в полном объеме изучить сложные процессы.
Данная статья — это фрагмент работы, в которой в свою очередь была предложена и исследована модель замкнутого пространства. После чего, на основе вводимой модели пространства, рассмотрены процессы в различных областях знаний, вопросы в области электродинамики, физиологии, описываются сердечнососудистая система человека, процесс мышления.
В статье нами предпринята попытка рассмотреть вопросы физиологии головного мозга в контексте с моделью нашего пространства, что в перспективе возможно позволит связать накопленный математический аппарат с изучением процессов физиологии в целом и процесса мышления в частности.
Сделать это предлагается, путем наложения структуры рассматриваемых процессов на элементы предложенной модели пространства.
Ключевые слова: моделирование, физиология, модель пространства, направленность внимания, объект внимания, числовой потенциал, процесс мышления
- Введение.
За основу для нашего анализа был взят фрагмент модели пространства S, определена структура модели, рассмотрены отдельные ее свойства.
После чего разобран пример процесса мышления человека, посредствам наложения структуры рассматриваемого процесса на модель нашего пространства.
Цель исследования— это попытка синтеза и комплексного рассмотрения сложнейших физиологических процессов: восприятия, воображения, памяти, внимания, изучение общих закономерностей процесса мышления. Попытка предложить качественно новый подход в изучения рассмотренных процессов.
- Материалы иметоды исследования.
В качестве материала для нашего исследования была разработана модель пространства, в статье частично рассмотрена ее структура, показаны отдельные ее свойства. Основным методом исследования является аналогия т. е., наложение структуры рассматриваемых процессов на элементы модели пространства.
- Результаты.
Рассмотрим модель пространства в горизонтальной плоскости α, где определена криволинейная сеть, состоящая из семейства прямых и окружностей.
Области на плоскости α будут направлены в соответствии с направленностью прямых и дуг на которых они находятся. Ось Y (или EW) будет являться двусторонней и области, к ней прилегающие будут иметь противоположные направления относительно друг друга.
В соответствии с направленностью областей заключим в них числовые ряды от 1 до 9, в интервале между особыми или назовем их критическими точками (D, V, E, W, O). В области, к которым прилегают критические точки заключим число 0. (рис. 1).

Направленность таких рядов будет находится во взаимозависимости с направленностью областей, в которые они заключены.
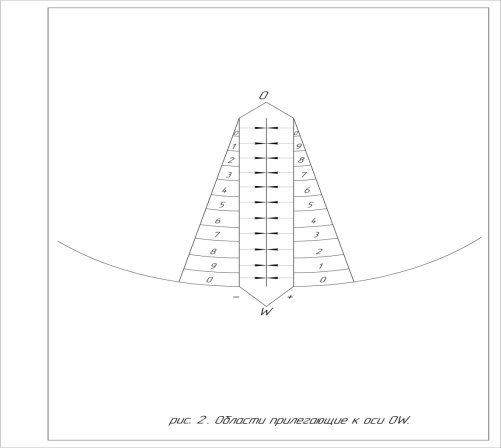
Из рисунка 2 мы видим, что числовые ряды, прилегающие к оси (Y), расположены если так можно выразиться, в числовой асимметрии. К примеру, область со значением 9 накладывается на 1, 8 на 2 и т. д.
В прямой аналогии с тем, когда одноименные электрические заряды между собой отталкиваются, а разноименные притягиваются.
В данном случае притягиваются не заряды, а области с разноименными числовыми значениями (или так скажем противоположными потенциалами).
Важным свойством здесь является свойство притяжения областей с противоположными числовыми потенциалами.
Мы видим, что числовые области граничат друг с другом таким образом, что их наложение друг на друга дает в сумме ноль. Точка W будет двусторонней, где максимум будет накладываться на минимум (max/min).
Теперь предложенный фрагмент модели пространства мы попробуем связать с процессами из области физиологии, в частности смоделируем процесс мышления человека.
По средствам аналогии, т. е., путем наложения структуры рассматриваемых процессов на модель нашего пространства.
Для этого рассмотрим прямую (Y) или OW и области с числовыми рядами к ней прилегающими.
Всю информацию мы условно можем классифицировать на 2 вида.
1) Информация, получаемая от внешних объектов, которую мы получаем в виде ощущений: зрительных, слуховых, вкусовых, обонятельных осязательных.
То есть восприятие, которое свяжем с числовым рядом, прилегающим к положительной части OW и заключим в интервале между двумя критическим точками (W+/O)
2) Информация, получаемая от внутренних объектов или из памяти, то есть воображение, которое свяжем с числовым рядом, прилегающим к отрицательной части WO и заключим в интервале между двумя критическим точками (W-/O). Эти два ряда являются параллельными и противоположно направленными. (рис 3).

Эти два числовых ряда наложены друг на друга таким образом, что максимум одного накладывается на минимум другого и наоборот (max/min).
Теперь, с движением по оси (Y) к примеру, точки P, мы можем связать внимание.
Возрастание внимание по отношению к внешним объектам будет сопровождаться снижением внимания к внутренним объектам и наоборот.
Теперь необходимо классифицировать объекты, воздействующие на наше сознание. (рис.4).

Цвета мы можем классифицировать в зависимости от яркости от минимальной к максимальной и заключим в интервал от O (0) ![]() D (
D (![]() ).
).
Звуки аналогичным образом классифицируем исходя из громкости от минимальной к максимальной и заключим в аналогичный интервал от O (0) ![]() D (
D (![]() ).
).
Вкусовые, обонятельные, осязательные ощущения, исходя из силы воздействия так же заключим в интервал от O (0) ![]() D (
D (![]() ).
).
В данном случае, нами рассмотрена лишь один из видов классификации для описания принципа моделирования.
Так же данные объекты (цвета, звуки, вкусовые, обонятельные, осязательные ощущения) мы можем классифицировать в зависимости от диапазона. К примеру цвета (красный, оранжевый, зеленый, голубой, синий, фиолетовый) мы можем заключить в аналогичный интервал, с каждым цветом связав соответствующую единичную точку в интервале от O (0) ![]() D (
D (![]() ).
).
Теперь исходя из поведения точки P на прямой OW, и которая нами ранее была связана с вниманием, мы проследим пример процесса мышления. (рис.5).
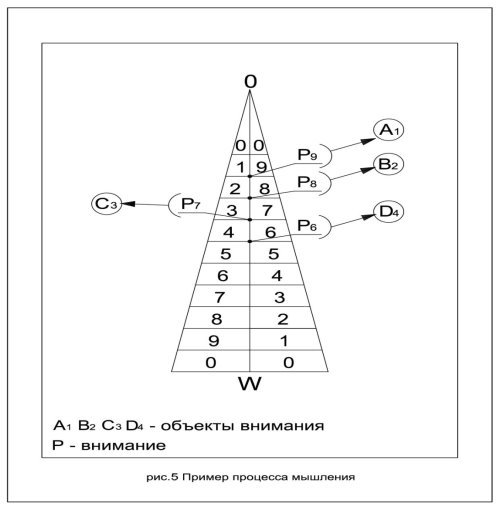
К примеру, в момент времени t1 внимание (P9) сконцентрировано на внешнем объекте (А1). С объектом (А1) мы можем связать чашку кофе. Внимание со значением — (P9) направлено на объект с потенциалом (А1).
В момент времени t2 внимание (P8) притягивает объект с большим потенциалом (В2). С объектом (В2) мы можем связать песню, звучащую по радио. Внимание со значением P8 направлено на объект с потенциалом (В2). Внимание переключилось с объекта (А1) на объект (В2) в силу того, что объект (В2) обладал большим потенциалом относительно объекта (А1), в момент времени t2.
В момент времени t3 внимание аналогичным образом (P7) притягивает внутренний объект (С3). Внимание со значением P7 направлено на объект с потенциалом (С3). С объектом (С3) мы можем связать ассоциацию, вызванную внешним объектом (В2). К примеру, музыка вызвала мысленный образ связанный, к примеру, с воспоминанием о работе. Внимание переключилось с объекта (В2) на объект (С3), так как объект (С3) обладал большим потенциалом относительно объекта (В2) в момент времени t3.
В момент времени t4 внимание становится (P6) переключается на внешний объект (D4). С объектом (D4) мы свяжем ассоциацию, вызванную внутренним объектом (С3). К примеру, воспоминания о работе побудили субъекта открыть книгу соответствующей тематики. Внимание переключилось с объекта (С3) на объект (D4). В силу того, что объект (D4) обладает большим потенциалом относительно объекта (С3) в момент времени t4.
Внимание, таким образом, всегда будет концентрироваться на объекте с большим потенциалом.
Напрашивается прямая аналогия с электричеством, где разность потенциалов обуславливает процесс движения зарядов по пути наименьшего сопротивления.
- Дискуссия.
Несмотря на обширный объем материала по вопросу математического моделирования в области физиологии в целом и процесса мышления в частности, перехода на качественно новый уровень в изучении данных сложнейших процессов нашего сознания на сегодняшний день добиться не удается. Большинство исследователей считают, возможность использования математического аппарата при описании психических процессов нашего сознания весьма отдаленной перспективой.
Вместе с тем считаю, что предложенный подход позволяет рассматривать процессы мышления в комплексе, показывает их общую и взаимозависимую природу. Рассчитываю, что предложенные идеи внесут новый импульс в изучение и понимание рассмотренных вопросов.
- Заключение.
В ходе исследования нами был предложен принцип математического моделирования, разобран пример процесса мышления человека, посредством аналогии т. е., наложения структуры рассматриваемого процесса на модель нашего пространства.
Все изложение материала было произведено при минимуме математических выкладок, что должно придать работе большую доступность.
Поставленная цель исследования достигнута, а именно предложен принцип моделирования в изучении фундаментальных физиологических процессов.
Вместе с тем рассчитываю, что предложенные идеи так же окажутся полезны для формирования общей картины научных процессов.
Литература:
- Атанасян, Л.С., Базылев. В. Т. Геометрия. Учеб пособие в 2 ч., ч 2 — М: Просвещение, 1987 г.
- Бахвалов С. В., и др. Аналитическая геометрия. Учебник. Москва 1962 г.
- Виноградов. И.М., Аналитическая геометрия — М: Наука 1986 г.
- Гильберт Д., Кон-Фосен С. Наглядная геометрия — М: Наука, 1981– 344 с.
- Гордон В. О., и др. Курс начертательной геометрии. М:, Наука 1964 г.
- Лансберг Г. С. Элементарный учебник физики: Учебное пособие в 3-х т., Т- 2. Электричество и магнетизм — М. Наука — 480 с.
- Лихин. А.Ф., Концепции современного естествознания: Учебник — М. проспект 2004–264 с.
- Маклаков А. Г., Общая психология. Учебник — СПб 2008–583с.
- Немов Р. С. Психология Учебник в 3 кн. Кн 1: Общие основы психологии — М, Виодос. 2003 г.
- Привес М. Г., Анатомия человека- 9-е изд. М, Медицина 1985 г. — 672 с.
- Сосновский Б. А. Психология: учебник — 2-е изд., М., Юрайт, 2011. -799 с.
- Чижов Е. Б. Пространства — М. Новый центр, 2001–278 с.







