Предлагаемая статья относится к области математической логики, моделирования, предлагается метод построения модели на примере сердечнососудистой системы человека.
Исследование биологических систем только в рамках физиологии или медицины не позволяет в полном объеме изучить сложные процессы.
Для нас является важным выявить и показать общие закономерности в различных областях знаний, что в свою влияет на формирование общей картины научных процессов.
Сделать это предлагается, путем наложения структуры рассматриваемых процессов на элементы предложенной модели пространства.
Рассчитываю, что предложенные идеи внесут новый импульс в изучение и понимание рассмотренных вопросов.
Ключевые слова: физиология,модель пространства, система кровообращения,область пространства, аналогия
Введение.
Данная статья — это фрагмент работы, в которой в свою очередь была предложена и исследована модель замкнутого пространства. После чего, на основе вводимой модели пространства, рассмотрены процессы в различных областях знаний, вопросы в области электродинамики, физиологии, описываются сердечнососудистая система человека, процесс мышления.
В настоящей статье рассматривается сердечнососудистая система человека, в контексте с элементами предложенного пространства.
Цель исследования— попытка на примере системы кровообращения человека предложитьпринцип создания математическое модели, сформулировать подход к изучению рассмотренных процессов.
Материалы иметоды исследования.
В качестве материала для нашего исследования была разработана модель пространства, в статье частично описана ее структура, показаны отдельные ее свойства. Основным методом исследования является аналогия т. е., наложение структуры рассматриваемых процессов на элементы модели пространства.
Результаты.
Рассмотрим систему кровообращения человека.
Кровь делится на венозную и артериальную, точно также как области пространства мы условно можем разделить на положительные и отрицательные. Существует два круга кровообращения большой и малый.
Большой круг кровообращения начинается с того, что кровь из левого желудочка через аортный клапан вбрасывается в аорту, после чего происходит деление на артерии и многочисленные капилляры. (рис.1)

Здесь мы можем аортный клапан связать с особой выталкивающей точкой D, а движение от аорты к капиллярам с направленностью областей на положительной полусфере, от минимума точки D к областям с большими значениями, к полюсам S и W. (рис 2 а,б)
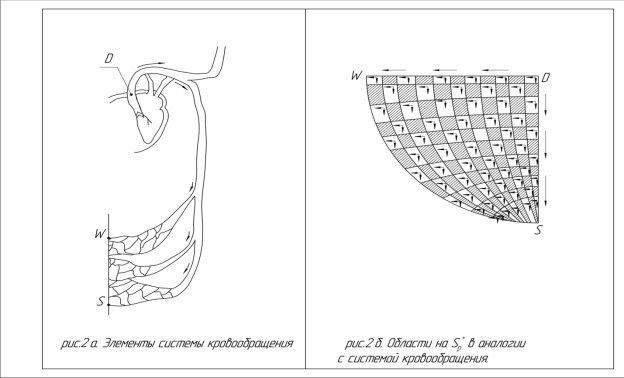
Что происходит дальше? Кровь из капилляров формирует венулы и кровь из артериальной переходит в венозную. Этот переход мы свяжем с движением по оси Y от точки W к точке E и переходом через точку О, из положительных областей пространства в отрицательные. (рис 3 а, б).
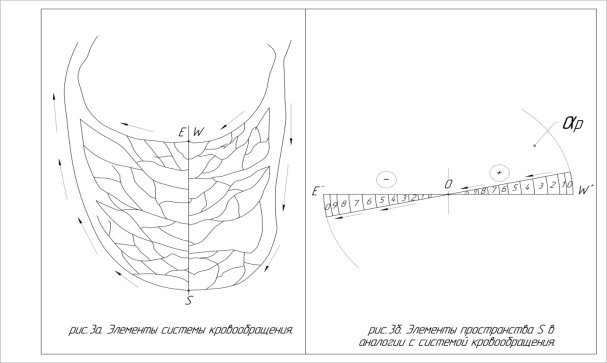
Затем венулы, собираются в вены, несущие кровь обратно в сердце.
Данную фазу движения мы свяжем движением областей на ![]() от дуги SE к особой втягивающей точке V. (рис 4 а,б)
от дуги SE к особой втягивающей точке V. (рис 4 а,б)
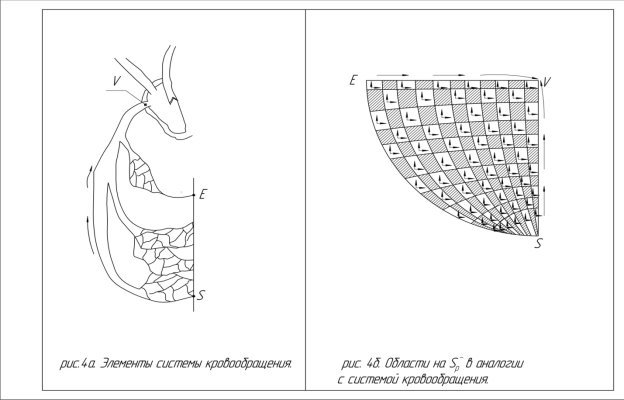
Восточную часть прямой VO и области к ней прилегающие (элемент 4) (рис 5. б) мы отождествим с правым предсердием, а правый желудочек рассмотрим в аналогии с областями прилегающими к восточной части прямой ОD (элемент 3, рис 5 б).
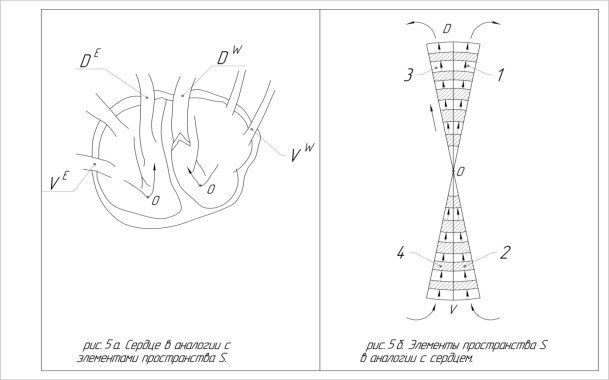
Здесь заканчивается большой и начинается малый круг кровообращения.
Аналогичным образом элементы малого круга кровообращения мы рассмотрим в аналогии с элементами модели S.
В свою очередь, области западной часть прямой VО мы свяжем с левым предсердием, (элемент 2), а левый желудочек рассмотрим а аналогии с областями западной части прямой ОD (элемент 1) (рис 5 б).
Предсердно-желудочковые клапаны левого и правого предсердия мы свяжем с точкой О. (рис 5 а).
Для нас здесь важно проследить аналогию системы кровообращения с векторной направленностью пространства S.
Заключение.
В ходе исследования нами был предложен принцип математического моделирования, рассмотрена система кровообращения человека, посредством аналогии т. е., наложения структуры рассматриваемого процесса на модель нашего пространства.
Вместе с тем рассчитываю, что предложенные идеи так же окажутся полезны для формирования общей картины научных процессов.
Литература:
- Атанасян, Л.С., Базылев. В. Т. Геометрия. Учеб пособие в 2 ч., ч 2 — М: Просвещение, 1987 г.
- Бахвалов С. В., и др. Аналитическая геометрия. Учебник. Москва 1962 г.
- Виноградов. И.М., Аналитическая геометрия — М: Наука 1986 г.
- Гайворонский И. В. Нормальная анатомия человека. Учебник для мед. вузов в 2 томах. — М, 1997.
- Гильберт Д., Кон-Фосен С. Наглядная геометрия — М: Наука, 1981г.
- Липченко В. Я., Самусев Р. П. Атлас нормальной анатомии человека. М., 1988.
- Лихин. А.Ф., Концепции современного естествознания: Учебник — М. проспект 2004–264 с.
- Привес М. Г., Анатомия человека- 9-е изд. М, Медицина 1985 г. — 672 с.
- Чижов Е. Б. Пространства — М. Новый центр, 2001–278 с.







