Ключевые слова: тестирование, мобильное приложение, метод тестирования, расширенный конечный автомат
С каждым годом рынок мобильных приложений постоянно увеличивается: системные и дополнительные утилиты, приложения на базе оповещений. Но к какому бы типу эти приложения не относились, каждое из них должно быть хорошо протестировано. На первый взгляд кажется, что тестирование мобильных приложений достаточное простое, ведь приложение чаще всего состоит лишь из нескольких экранов-страниц. Но вся суть в том, что новые версии мобильного приложения разрабатываются и собираются во много раз чаще, чем веб-приложения или десктоп-приложения, и, как следствие, приемочное тестирование выполняется очень часто. Довольно обыденно становится для тестировщика повторять однотипные действия: установить приложение, запустить, проверить, что все необходимые элементы присутствуют и т. д. Средства для Android-приложений были выбраны темой исследования неслучайно: устройства отличаются большим разнообразием и тестирование необходимо выполнять на каждом из них (устройства могут отличаться версиями операционной системы, разрешением экранов, наличием или отсутствием фронтальной камеры и др.). То есть, если рассматривать iOS-устройства, то в таком случае процесс тестирования немного упрощается, так как произвести проверку необходимо только на некоторых устройствах: iPhone, iPad, iPod для конкретных версий ОС [1].
В контексте тестирования приложений для мобильных устройств (ПМУ) на системном уровне, взаимодействие конечного пользователя и ПМУ можно разбить на следующие типы:
Взаимодействие с элементом UI (пользовательского интерфейса), который не предусматривает ввод данных (детерминированный элемент). В дальнейшем будем называть такой тип — «детерминированное действие» (ДД). Множество различных ДД напрямую зависит от разнообразия типов элементов интерфейса ПМУ и способов действия на них и является конечным числом.
Взаимодействие с элементом UI, который предусматривает ввод данных (поля ввода, формы и др.). В общем случае пользователь может ввести в приложение любой набор данных, это предполагает бесконечное число подобных действий ввода данных. Любое действие, связанное с вводом данных будем обозначать типом «вариационное действие» (ВД).
Определив конечный набор детерминированных действий, и ограничив бесконечный набор вариационных действий конечным набором, можно свести взаимодействие пользователя с ПМУ к детерминированному, конечному набору операций.
Во всех мобильных операционных системах (Android, iOS, Symbian, Blackberry и др.) существует определенный, конечный набор элементов пользовательского интерфейса. Большинство типов элементов одинаково для всех ОС, поэтому можно задать общий для всех операционных систем, конечный набор детерминированных действий. Для каждой конкретной операционной системы данный набор может быть расширен с учетом элементов, не вошедших в пересечение элементов интерфейса всех операционных систем. Такой набор позволяет формально описывать взаимодействия типа «детерминированное действия» в унифицированном виде (в независимости от типа операционной системы). Очевидно, что существует некоторое отображение элементов UI на действия, которые можно совершить с данными элементами. Обозначим его action(ed). Это отображение возвращает набор действий, которые применимы для данного элемента UI∙ed, который предполагает конечный, детерминированный набор действий с собой. Введенное отображение будет использовано позднее при определении расширенного конечного автомата для ПМУ.
В общем случае пользователь может ввести в приложение любой набор данных. Для ограничения данного числа наборов предлагается воспользоваться принципом эквивалентного разбиения вводимых данных [2]. В соответствии с этим принципом необходимо все данные, которые может ввести пользователь в данный набор элементов UI, предполагающих ввод данных разделить на несколько классов. На всех данных из заданного класса эквивалентности приложение ведет себя одинаково. Обозначим V = ={еv1,еv2,..,еvl) — набор всех вариационных элементов UI, которые видит пользователь в текущем состоянии приложения, evобозначает вариационный элемент UI, который предполагает ввод данных.
В общем случае число классов эквивалентности конечное число. Рассмотрим пример: допустим, в некотором состоянии приложения существует набор вариационных элементов интерфейса. В зависимости от данных, которые можно ввести получаем следующий набор классов эквивалентности.
Приложений для мобильных устройств разрабатываются с использованием принципа отделения логики работы приложения и представления (пользовательского интерфейса). Особенности данного принципа и рассматриваемая метрика тестирования ПМУ позволяют использовать конечные автоматы для формального описания прототипов приложений для мобильных устройств [3].
При анализе существующих мобильных приложений было выявлено, что количество основных видов приложений — конечное небольшое число (не более 100), но переход в каждый вид может зависеть от вводимых конечным пользователем данных. Возникает проблема «размножения» одинаковых видов при вводе «однотипных» данных. Действительно, допустим в данном виде существует некоторая форма ввода, которая принимает любые строковые значения на вход и после отправки данных «в приложение», происходит переход к следующему виду, в котором отображаются введенные данные. При построении соответствующего конечного автомата (КА) получаем бесконечное число состояний. Размножение числа состояний представлено на рисунке 1.
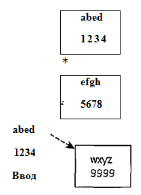
Рис. 1. Размножение состояний конечного аппарата
Решение этой проблемы состоит в разбиении всех вводимых данных на классы эквивалентности, это ограничит число «конечных» состояний. Вторая проблема, которая возникает при построении КА для ПМУ — зависимость «будущих» переходов от вводимых данных в «текущем» переходе. Например, в случае существования ролевой модели в приложении, переход к некоторым видам может быть «закрыт» для пользователей одних ролей и открыт для пользователей других ролей (рис. 2):
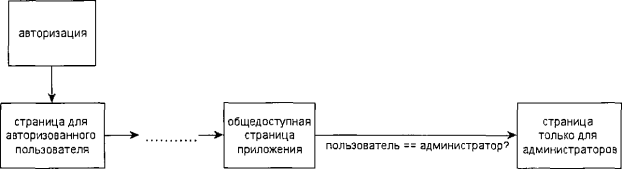
Рис. 2. Пример условия на переходе конечного автомата
При построении КА такого приложения возникает необходимость «запоминать» под каким пользователем мы вошли в систему и «проверять» запомненное значение при каждой попытке перейти в состояние, требующее определенных прав.
Решение этой проблемы состоит в разбиении всех вводимых данных на классы эквивалентности, это ограничит число «конечных» состояний. Вторая проблема, которая возникает при построении КА для ПМУ — зависимость «будущих» переходов от вводимых данных в «текущем» переходе.
Решение этой проблемы заключается в использовании расширенного конечного автомата для построения прототипа приложения. Такой способ задания КА позволит «запоминать» необходимые данные в виде параметров РКА и проверять значения этих параметров при переходе к «закрытым» страницам, предварительно задав условия на переходах.
«Расширенная конечно-автоматная модель — это усовершенствованная модель конечного автомата. В традиционном конечном автомате переход из состояния в состояние связан с набором входных булевых условий и набором выходных булевых функций. В расширенной модели переход может быть выражен «IF» выражением. Если все условия перехода соблюдены, то происходит переход, переводя автомат в следующее состояние, при этом производятся требуемые операции с данными» [3]. Формально: «расширенный конечный автомат — набор (S, V, P, s0, P0, I, n1, X, 0, n0, Y, T), где:
S — конечное множество состояний автомата;
V — множество, возможно бесконечное, значений внутренних данных автомата;
Р — отображение конечного набора [1..n] индексов в W,Р: [1..N] —>W; значение Р на индексе i называется значением i-ой переменной автомата, которое также обозначается рi.
s0 — элемент S, называемый начальным состоянием;
Р0 — отображение [1..n] индексов в W, называемое начальными значениями переменных;
I — конечное множество, элементы которого называются операциями или стимулами, само I называют входным алфавитом автомата;
n1 — отображение I в неотрицательные числа, определяет число параметров для каждого стимула;
X — множество, возможно бесконечное, значений параметров стимулов;
О — конечное множество, элементы которого называются реакциями, само О называют выходным алфавитом автомата;
n0 — отображение О в неотрицательные числа, определяет число параметров или данных каждой реакции;
Y — множество, возможно бесконечное, значений данных реакций;
Т — множество переходов автомата; каждый переход t включает начальное управляющее состояние s1, стимул I, условие перехода gt (guard condition) — предикат на множестве Vn×Xni, конечное управляющее состояние s2, и действие at — некоторое отображение Vn×Xni во множество Vn, определяющее новые значения переменных.
Выполнение расширенного автомата отличается от выполнения обычного тем, что помимо текущего состояния имеются текущие значения переменных, при подаче стимула с набором аргументов охранное условие определяет, может ли быть выполнен данный переход при текущем наборе значений переменных и заданных значениях параметров стимула. Выполняемый переход выбирается не детерминировано из всех, помеченных данным стимулом, начинающихся в данном управляющем состоянии и имеющих выполненное охранное условие. При выполнении некоторого перехода новое управляющее состояние автомата равно конечному управляющему состоянию перехода, новые значения переменных определяются при помощи его действия — новое pi = at(p1..., рn, х1..., xn1), значения параметров реакции — по соответствующему отображению в переходе» [4].
Литература:
1. Кабылова Д. А., Когай Г. Д., Ашимова Д. Е. Метрика тестового покрытия приложений для мобильных устройств: Тезис/Труды Международной научно-практической конференции «Интеграция науки, образования и производства — оснава реализации Плана нации», Караганда, КарГТУ 2016.
2. Степанченко И. В. Эквивалентное разбиение. Методы тестирования программного обеспечения: РПК «Политехник», Волгоград 2006.
3. Хатько Е. Е. Об одном методе тестирования «мобильных» приложений: Труды МФТИ, 2012 г.
4. Кулямин В. В. Тестирование на основе моделей, http://panda.ispras.ru. [В Интернете] http://panda.ispras.ru/~kuliamin/lectures-mbt/Lecture04.pdf.







