В статье приводится алгоритм расчета короткого напорного трубопровода и его реализация в MSExcel. Задача нахождения диаметра трубопровода, обеспечивающего требуемый расход, решается методом подбора.
Ключевые слова: короткий трубопровод, гидравлические сопротивления, число Рейнольдса, режим движения жидкости
Введение. Одной из основных задач курса гидравлики является расчет короткого напорного трубопровода. Важность задачи обусловлена широким применением коротких трубопроводов, к которым можно отнести сифонные трубопроводы, всасывающие трубы насосов, дюкеры, части трубопроводов внутри зданий и сооружений и пр.
Короткий трубопровод — трубопровод достаточной малой длины, в котором потери напора в местных сопротивлениях составляют более 10 % от потерь напора по длине [1, с. 215]. В связи с этим при расчете короткого трубопровода необходимо учитывать как потери напора по длине, так и местные потери напора.
Расчет короткого трубопровода сводится к решению одной из трех задач (рис. 1).
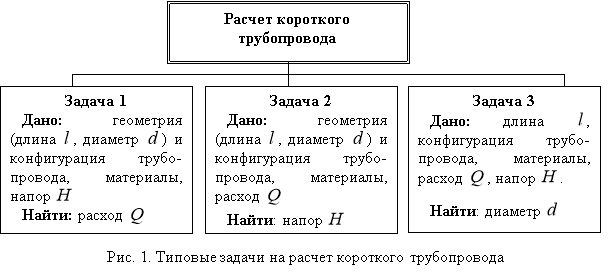
Наибольшие сложности вызывает решение третьей задачи, так как в большинстве случаев определить диаметр короткого трубопровода можно только методом подбора.
Алгоритм расчета диаметра короткого напорного трубопровода методом подбора. Рассмотрим общий алгоритм решения поставленной задачи. Вычисления в соответствии с представленным алгоритмом в ручном режиме являются достаточно затратными по времени. Существенно упростить работу по расчету диаметра трубопровода методом подбора позволяет реализация алгоритма в какой-либо программной среде. При этом самым простым вариантом, не требующим специальных навыков в области программирования, является MSExcel.
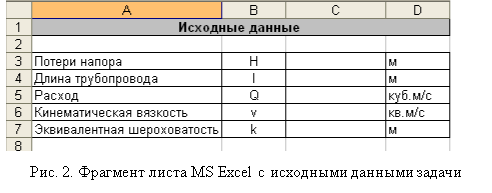
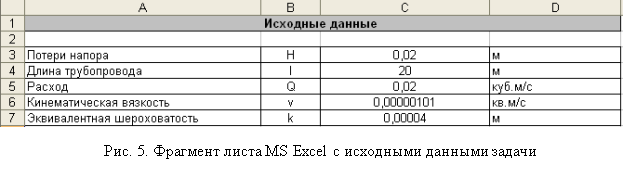
Этап 1. Зададим исходные данные, известные по условию задачи. К исходным данным следует отнести (рис. 2): потери напора (перепад уровней жидкости) (
, м); длину трубопровода (
, м); пропускную способность трубопровода (расход) (
, м); кинематическую вязкость жидкости (
, м2/с); эквивалентную шероховатость стенок трубопровода (
, м).
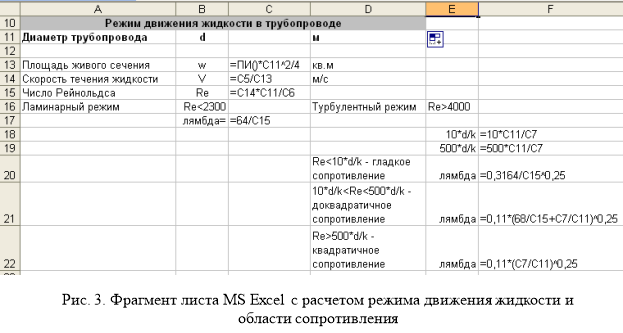
Этап 2. Зададим произвольным образом диаметр трубопровода 
и определим режим движения жидкости.
Вычислим площадь живого сечения 
трубопровода. Для упрощения рассуждений будем считать, что диаметр трубопровода по его длине не меняется, трубопровод имеет круглое сечение, полностью заполненное жидкостью:
|
|
(1) |
.
Рассчитаем скорость течения жидкости 
в трубопроводе:
|
|
(2) |
.
Определим режим движения жидкости в трубопроводе, для чего вычислим число Рейнольдса:
|
|
(3) |
.
При 
режим движения жидкости ламинарный, при 
– турбулентный.
Рассчитаем коэффициент гидравлического трения 
. Если режим движения ламинарный, то коэффициент 
определяют по формуле:
|
|
(4) |
.
Если режим движения турбулентный, то дополнительно нужно определить область сопротивления. Для этого по материалу, из которого изготовлен трубопровод, и сроку его службы нужно найти эквивалентную шероховатость стенок трубопровода 
[2, с. 72].
Если 
, то трубопровод следует отнести к области гладкого сопротивления. В этом случае коэффициент 
может быть рассчитан по формуле Блазиуса:
|
|
(5) |
.
Если 
, то область сопротивления является доквадратичной и для расчета коэффициента 
используется формула Альтшуля:
|
|
(6) |
.
Если 
, то область сопротивления квадратичная и для нахождения коэффициента 
можно применить формулу Шифринсона:
|
|
(7) |
.
Этап 3. Рассчитаем потери напора в трубопроводе при заданном диаметре. Полные потери напора в трубопроводе состоят из потерь напора по длине и потерь напора в местных сопротивлениях:
|
|
(8) |
.
Потери напора по длине 
определим по формуле Вейсбаха-Дарси:
|
|
(9) |
.
Потери напора в местных сопротивлениях 
вычислим по формуле Вейсбаха:
|
|
(10) |
,
где 
— коэффициент местного сопротивления, который зависит от вида местного сопротивления и его геометрии.
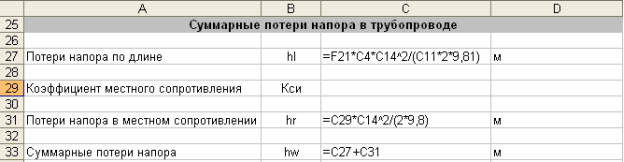
Рис. 4. Фрагмент листа MS Excel с расчетом суммарных потерь напора
Этап 4. Сравним рассчитанные суммарные потери напора в трубопроводе 
с потерями напора 
, заданными по условию задачи. Если 
, то значение диаметра выбрано верно. Если же 
, то значение диаметра нужно изменить и повторить все вычисления.
Пример решения задачи на расчет короткого напорного трубопровода.
Задача. Трубопровод из стальных новых труб длиной 20 м присоединен к напорному баку, заполненному водой при температуре 20ºС. После полного открытия вентиля расход воды в трубопроводе оказался равным 20 л/с, а разность уровней воды в напорном резервуаре и пьезометре составила 2 см. Определите диаметр трубопровода.
Для решения задачи воспользуемся приведенным выше алгоритмом.
Зададим исходные данные. Коэффициент кинематической вязкости воды при
приведен по справочнику [2, с. 16], коэффициент эквивалентной шероховатости стальных новых труб — по справочнику [2, с. 72].
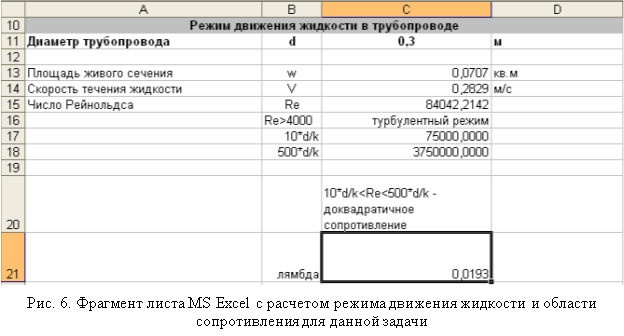
Зададим произвольным образом диаметр трубопровода 
и определим для указанного диаметра режим движения жидкости.
Так как число Рейнольдса 
, то режим движения турбулентный. Далее, используя значение эквивалентной шероховатости, определим область сопротивлений. Так как 
, то область сопротивления доквадратичная и для расчета коэффициента гидравлического трения 
следует использовать формулу Альтшуля (6). В итоге расчетов получаем 
.
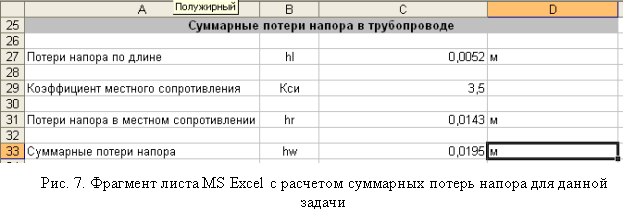
По формулам (8), (9), (10) рассчитаем потери напора в трубопроводе. В рассматриваемой задаче имеются два местных сопротивления: внезапное сужение потока при переходе из напорного резервуара в трубопровод (
) и вентиль, который полностью открыт (
).
Из проведенного расчета видно, что суммарные потери напора по длине трубопровода 
примерно совпадают с потерями напора (разностью уровней воды в резервуаре и пьезометре), заданными по условию задачи 
. Следовательно, диаметр трубопровода выбран верно.
Однако найденное значение диаметра можно уточнить. Если задать значение диаметра 
, то расчетные суммарные потери напора в трубопроводе составят 
.
Выводы. Представленный в статье алгоритм определения диаметра короткого напорного трубопровода и его реализация в MSExcel предназначены в первую очередь для студентов строительных направлений подготовки, изучающих гидравлику. Реализация алгоритма средствами MSExcel достаточно проста и позволяет наглядно проследить основные этапы расчета трубопровода. Вместе с тем, применение табличного редактора существенно экономит время проведения типовых расчетов.
Литература:
- Чугаев Р. Р. Гидравлика: учебник для вузов. — Л.: Энергоиздат, 1982.
- Вильнер Я. М. Справочное пособие по гидравлике, гидромашинам и гидроприводам / Я. М. Вильнер, Я. Т. Ковалев, Б. Б. Некрасов, под ред. Б. Б. Некрасова. — Минск, 1976.
