В статье проведен анализ влияния настроечных параметров системы автоматического регулирования возбуждения (АРВ) на переходные процессы. С использованием технологии вложения систем получены передаточные функции исследуемой модели электрической системы, ее полюса и нули. Рассмотрено влияние параметров системы АРВ на электромагнитные и электромеханические колебания.
Ключевые слова: электроэнергетическая система, автоматический регулятор возбуждения, технология вложения систем, переходные процессы
Настоящий этап развития энергетики характеризуется наличием соединенных относительно слабыми связями крупных концентрированных энергосистем, в состав которых активно включаются мощности распределенной генерации. Изменение состава генерации и структуры электропотребления приводит к уменьшению постоянных инерции элементов энергосистем, повышая чувствительность параметров режима энергосистемы в целом к небольшим возмущениям. Поэтому в целях повышения управляемости энергосистем внедряется новое оборудование, оснащенное современными быстродействующими устройствами регулирования возбуждения и частоты, в узловых точках электрической системы АРВ снабжаются системными стабилизаторами, применяются устройства FACTS, накопители энергии и др. [1].
Низкочастотные составляющие (f≈0,2÷1,5 Гц) характеризуют колебания ротора синхронной машины и зависящих от них режимных параметров (углов расхождения роторов δ, мощностей, токов статора) электрической системы (ЭС). Относительно высокочастотные (f>1,5 Гц) большие колебания проявляются в системах регулирования возбуждения при практическом отсутствии колебаний ротора и тока возбуждения [2].
Они получили название электромагнитных колебаний, так как обусловлены электромагнитными контурами АРВ.
В результате, помимо полезных эффектов энергосистема приобретает также и некоторые негативные свойства, проявляющиеся, в частности, в возникновении низкочастотных (0,1÷3,0 Гц) общесистемных колебаний ее режимных параметров. Важность и сложность задачи обеспечения устойчивости энергосистем при возникновении таких колебаний привели к необходимости разработки новых методов ее оценки, основанных на тщательном изучении динамических свойств энергообъединений. В их число входят также методы технологии вложения систем [3], позволяющих глубоко исследовать колебательные свойства ЭЭС, в том числе и при малых колебаниях в них [2].
Как было отмечено выше, динамические свойства энергосистемы характеризуются многочастотностью. Среди них содержатся как локальные, так и охватывающие практически всю энергосистему, общесистемные колебания.
Многочастотность колебаний с существенно различными частотами и коэффициентами затухания определяется наличием динамических элементов с разными постоянными времени. Каждая частотная составляющая проявляется по-разному в различных режимных условиях.
Такое разделение колебаний физически объясняется тем, что обмотка возбуждения имеет большую постоянную времени (4 с), а ротор синхронной машины—значительную механическую инерцию, вследствие чего составляющие колебания высокой частоты практически не проявляются в колебаниях ротора, иными словами, ротор является фильтром высоких частот.
Колебания снижают надежность и эффективность эксплуатации электрических систем и могут привести к системным авариям [2].
Как правило, в сложной электрической системе, учет и регулирование АРВ производится по следующему алгоритму. АРВ всех станций (эквивалентные генераторы) учитываются с постоянными э. д.с. или постоянством напряжений на шинах, а АРВ регулируемой станции учитываются более полно с дифференциальными уравнениями или передаточными функциями. После определения параметров АРВ данной станции, считая их постоянными, переходят к определению параметров других станций. По существу, каждый раз параметры АРВ исследуемой станции определяются по схеме «генератор-шины».
При анализе переходных процессов исследуемой модели электрической системы будем использовать линеаризованные уравнения простейшей ЭС при наличии на синхронном генераторе автоматических регуляторов возбуждения имеют вид [1]:
‒ уравнение относительного движения ротора синхронной машины:
j(d2/dt)= — d(d/dt) —
‒ уравнение переходных процессов в обмотке возбуждения:
d(q/dt)= qe — q;
‒ уравнение в обмотке возбуждения возбудителя:
Te(qe/dt)=kee-qe;
‒ уравнение усилительного элемента: (1)
Ty(e/dt)=kyu-e;
‒ уравнение измерительного элемента:
TИ(du/dt)=kuuг-u;
‒ уравнение, отражающее влияние АРВ:
е = 
(k0Пj∆Пj+k1Пj(dПj/dt)+k2Пj(d2Пj /dt2)),
здесь — j, d, e, У, И — постоянные инерции агрегата, постоянные времени соответственно — обмотки возбуждения при разомкнутой обмотки статора, возбудителя, усилительного элемента, преобразовательного и измерительного элементов (ТИ = ТП); , q, q, qe, е, u, uг — отклонения — угла нагрузки, переходной э. д.с., э.д.с. холостого хода, э.д.с. на кольцах ротора, на обкладках возбудителя и напряжения на шинах генератора; Пj — параметры режима, по которым осуществляется регулирование возбуждения генератора; Pd — демпферный коэффициент; k0Пj, k1Пj, k2Пj — коэффициенты усиления по каналам регулирования АРВ соответственно — по отклонению [ед.возб/ед.П], по первой и второй производным [ед.возб.сек/ед.П], [ед.возб.сек2/ед.П].
Расчеты будем проводить для простой электрической системы, схема которой приведена на рис.1.
Рис. 1. Схема эквивалентной электрической системы
Система уравнений (1) приводится к виду:
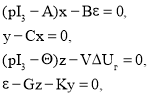(2)
где
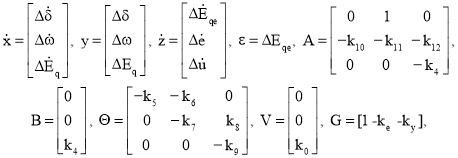
K = [k0б k1б k0u], С=I3.
При этом регуляризирующее уравнение имеет вид:
= ∆qе = ke∆e + ky∆u + k0∆ + k1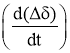 
+ k0u∆UГ.
Здесь ke, ky — коэффициенты усиления каналов АРВ.
В системе уравнений (2): А — матрица, определяемая коэффициентами математической модели синхронного генератора, В — матрица входа, , V, G — матрицы АРВ, К — матрица, определяет закон регулирования АРВ, С — матрица, характеризует выход системы. Необходимо отметить, что матрицы вложения 
, 
, С должны быть согласованы с матрицей В [3].
В случае регулируемой системы суммарную передаточную функцию-скалярный образ, можно получить в виде [3]:
(3)
где
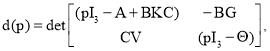(4)
‒ знаменатель передаточной функции скалярного образа, характеристический определитель системы определяет полюса исследуемой системы и
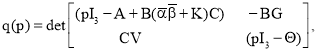(5)
‒ числитель передаточной функции скалярного образа, определяет нули исследуемой системы.
В целях интегрированного учета действия по всем каналам АРВ (отклонения угла нагрузки, напряжения на шинах генератора и первая производная по углу), матрицы вложения зададимся в виде:
(6)
тогда формула скалярного образа имеет вид:
(7)
где дополнительные обозначения определяются:
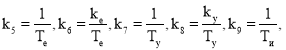
d0 = 1, q0 = A10,
d1 = A1+A4, q1 = A11+A4A10,
d2 = A2+A4+A1A4, q2 = A12+A4A11+A5A10,
d3 = A3+A6+A1A5+A2A4, q3 = A5A11+A4A12+A6A10,
d4 = A1A6+A2A5+A3A4, q4 = A6A11+A5A12,
d5 = A2A4+A3A5, q5 = A6A12.
d6 = A3A6,
A1=k11+k4(1+k0U), A7=k11+k4+k4(1+k0U),
A2=k4k11+k0Uk4(1+k11)+k4-k4k12k1, A8=k10+k11 [k4+k4(1+k0U)]-k4k12(1+k1),
A3=k4k10(1+k0U)-k4k12k1, A9=k10 [k4+k4(1+k0U)]-k4k12(1+k0),
A4=k7+k9, A10=A7-A1,
A5=k5(k7+k9)+k7k9, A11=A8-A2,
A6=k5k7k9, A12=A9-A3.
Формула (7) позволяет провести исследования влияния параметров режима и системы регулирования на динамические свойства исследуемой регулируемой электрической системы.
В свете вышеотмеченного проведем исследование динамических свойств исследуемой простой электрической системы на основе формулы (7), для скалярного образа по технологии вложения систем [4]. Проверим, совпадут ли результаты, полученные на основе данной технологии, с известными результатами из теории и практики проектирования и эксплуатации современных АРВ.
Как отмечается в [2], при увеличении нагрузки снижаются частоты электромеханических колебаний параметров режима. На рис. 2 приведены соответствующие характеристики, при нагрузке генератора 0 = 700, в случае, когда каналы регулирования АРВ отключены (далее этот случай будем считать базовым).
Анализ показывает, что при данном режиме полюса системы: -67.7532; -2.0139 ±10.9887i; -1.3383±3.5362i; -0.0282, а нули системы: -33.3192 ± 8.1069i; 15.2409; 0.1695; -0.0283.
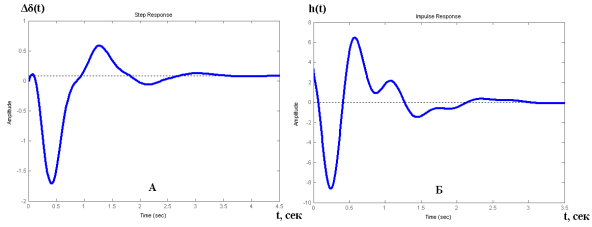
Рис. 2. Переходная (А) и импульсная (Б) характеристики исследуемой системы при параметрах: 0 = 700; q0 = 3; Рd = 0.1; Tj= 7 c.; 
= 0.3 с; Te= 1 c.; Ty= 0.03 c.; Tu=0.03 c.; x1=1.5; ke=1; ky=1; ku=1; k0= 0; k1= 0; k0u= 0
Как видно, колебания происходят как сумма колебаний двух частот определяемая:
(8)
(i=1,2), 
– электромеханические колебания системы, близкие к собственной частоте генератора (0.754 Гц), и вторая составляющая 
— электромагнитные колебания, определяемые системой АРВ.
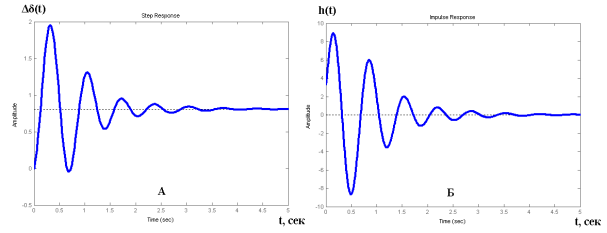
Рис. 3. Переходная (А) и импульсная (Б) характеристики исследуемой системы при тех же параметрах (рис.1), но 0 = 300.
На рис. 3. приведены соответствующие характеристики при уменьшении нагрузки генератора до 0 = 300. При данном режиме полюса системы: -67.7632; -1.2194 ± 9.4176i; -2.1278 ± 6.7386i; -0.0283, а нули системы: -33.3192±8.1069i; -5.9209±5.2617i; -0.0283. Соответственно, частоты колебаний составляют: f1=1.07 Гц и f2=1.5 Гц. Частота электромеханических колебаний с уменьшением нагрузки увеличилась.
На рис. 4. приведены соответствующие характеристики при включении всех каналов АРВ. При этом повышаются частоты и электромеханических (f1=0.775Гц), и электромагнитных колебаний (f2=2.877), по сравнению с базовым вариантом.
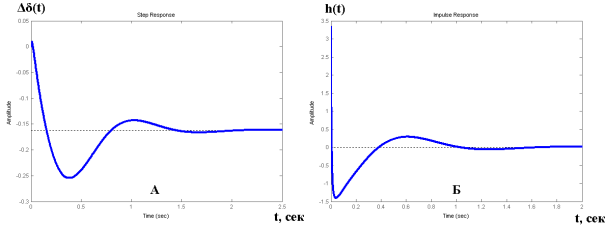
Рис. 4. Переходная (А) и импульсная (Б) характеристики исследуемой системы при тех же параметрах (рис.1), но k0= 10 ед.; k1= 1 ед.; k0u= 50.
Переходный процесс при этом затухает почти в два раза быстрее (~2.5с), так как декремент затухания в данном случае больше. Полюса системы: -179.29; -28.49±18.07i; -2.43±4.87i; -0.03, а нули: -69.0364; -33.3192±8.1069i; -3.6260; -0.0283.
Правильный (оптимальный) выбор настроечных каналов системы АРВ позволяет значительно увеличить пределы устойчивости ЭЭС, особенно введение каналов по производной угла позволяет снизить амплитуду и время протекания переходных процессов.
Литература:
- Аллаев К. Р., Мирзабаев А. М. Матричные методы анализа малых колебаний электрических систем. — Ташкент: «Fan va texnologiya», 2016. — 432 с.
- Литкенс И. В., Пуго В. И. Колебательные свойства электрических систем. — М.: Энергоатомиздат, 1988. — 217с.
- Буков В. Н. Вложение систем. Аналитический подход к анализу и синтезу матричных систем. — Калуга: Издательство Н. Ф. Бочкаревой, 2006. — 720 с.
- Махмудов Т. Ф. Технология вложения систем как метод анализа сложных систем // Одиннадцатая международная научно-техническая конференция студентов, аспирантов и молодых ученых «Энергия-2016». — Иваново: ФГБОУ ВО «Ивановский государственный энергетический университет им. В. И. Ленина», 2016. — С. 66–67.
