Коэффициент продуктивности скважин является одним из широко используемых параметров в практике разработки нефтяных месторождений. Правильное установление текущей величины этого параметра и закономерности его изменения во времени позволяющие надежно и достоверно прогнозировать ряд основных технологических показателей разработки залежей, представляется весьма важной задачей.
В данной работе предложена аналитические формулы для определения коэффициент продуктивности скважин по данном полученных от интерпретации индикаторных линий скважин, добывающих углеводороды с аномальными свойствами.
Особенность фильтрации вязко пластичной нефти, как известно состоит в том, что движение ее начинается после того, как градиент давления не превышает своего некоторого предельного значения, т. е.
![]() , (1)
, (1)
где G0 — начальный градиент давления, ![]() — предельное напряжение сдвига,
— предельное напряжение сдвига,
к — проницаемость пласта, ![]() — коэффициент равный 0,017 по данным работы [2,3,4]. Фильтрации в пористой среде нефтей с указанным свойствами чаще всего описывается обобщенным законом Дарси с начальным градиентом давления в виде:
— коэффициент равный 0,017 по данным работы [2,3,4]. Фильтрации в пористой среде нефтей с указанным свойствами чаще всего описывается обобщенным законом Дарси с начальным градиентом давления в виде:
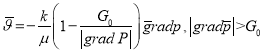 (2)
(2)
В скалярной форме она имеет вид:
![]() (3)
(3)
С учетом закона (3) рассмотрены различные фильтрационные задачи. Например с учетом (3) для расчета притока вязко пластичной нефти к скважине предложена следующая формула:
Из формулы (4) следует, что коэффициент продуктивности скважины увеличивается с увеличением депрессии следующим образом:
![]() (5)
(5)
На рис. 1 а дается графическое изображение зависимости (5).Как видно с увеличением ![]() , начиная с
, начиная с ![]() текущих коэффициент продуктивности скважины
текущих коэффициент продуктивности скважины ![]() увеличивается и приближается к А0 при достаточно большом значении
увеличивается и приближается к А0 при достаточно большом значении ![]() . Это обстоятельство использовано в [2,3,4] для объяснение вогнутых к оси дебитов форм индикаторных кривых. Между тем, в [6] установлено, что на вогнутые формы индикаторных кривых оказывает определенное влияние и изменение реальных свойств нефти от давлении и что при этом текущих коэффициент продуктивности становиться больше А0 (рис. 1 б).
. Это обстоятельство использовано в [2,3,4] для объяснение вогнутых к оси дебитов форм индикаторных кривых. Между тем, в [6] установлено, что на вогнутые формы индикаторных кривых оказывает определенное влияние и изменение реальных свойств нефти от давлении и что при этом текущих коэффициент продуктивности становиться больше А0 (рис. 1 б).
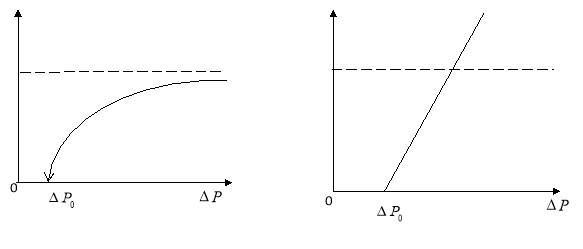
(а)(б)
Рис. 1 Зависимость q / ![]() от
от![]()
В работах [1,5]установлено что в этом случае для определения дебита скважины формула имеет следующий вид:
![]() f (p) dr (6)
f (p) dr (6)
А текущий коэффициент продуктивности
![]() (7)
(7)
Где
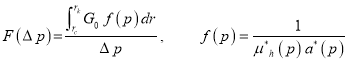 ,
,
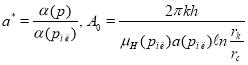 (8)
(8)
Здесь ![]() ,
, ![]() вязкость и объемный коэффициент нефти.
вязкость и объемный коэффициент нефти.
В работе установлено что несмотря на то что в общем случае уравнение (7) не является уравнением прямой, между тем, обработка промысловых данных исследования скважин в координатах ![]() от
от ![]() линейно зависит от депрессии (рис. 1 б.) Причем эти прямые как правило отсекают на оси депрессии отрезок, равный начальному перепаду давления (
линейно зависит от депрессии (рис. 1 б.) Причем эти прямые как правило отсекают на оси депрессии отрезок, равный начальному перепаду давления (![]() ). Однако проведенные исследования показывают что зависимость
). Однако проведенные исследования показывают что зависимость ![]() от
от ![]() pможет описывается прямой линией только при достаточно больших значениях депрессии. Это можно увидеть также из (7) где F
pможет описывается прямой линией только при достаточно больших значениях депрессии. Это можно увидеть также из (7) где F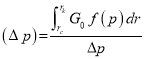 . Как видно при достаточно больших значениях
. Как видно при достаточно больших значениях![]() ,
, ![]()
![]() 0 в уравнении (7)
0 в уравнении (7) ![]() зависит от
зависит от![]() линейно, т. е. фактически влияние градиента теряется. Следовательно определение
линейно, т. е. фактически влияние градиента теряется. Следовательно определение ![]() по отрезку отсекаемой прямой линией в координат
по отрезку отсекаемой прямой линией в координат ![]() от
от ![]() является приблизительной. Для более точного определения притока флюида к одиночной скважине с учетом влияния изменения физических свойств флюида и коллектора для месторождений с начальным градиентом, примем что зависимость комплекса параметров от депрессии можно в наиболее общем случае аппроксимировать многочленом степени n, т. е.
является приблизительной. Для более точного определения притока флюида к одиночной скважине с учетом влияния изменения физических свойств флюида и коллектора для месторождений с начальным градиентом, примем что зависимость комплекса параметров от депрессии можно в наиболее общем случае аппроксимировать многочленом степени n, т. е. ![]() (9)
(9)
где![]() , с1, с2 ….., сn — коэффициенте характеризующие изменение комплекса параметров флюида и коллектора в зависимости от снижения давления и сопутствующих ему процессов. Следует отметить что для однофазной нефти, при отсутствии градиента давления
, с1, с2 ….., сn — коэффициенте характеризующие изменение комплекса параметров флюида и коллектора в зависимости от снижения давления и сопутствующих ему процессов. Следует отметить что для однофазной нефти, при отсутствии градиента давления
![]()
![]() (10)
(10)
Для жидкой фазы газированной нефти
![]() ,
, ![]() ,
, ![]() (11)
(11)
Здесь Р и ![]() - соответственно текущее давление и насыщенность коллектора флюидом в произвольной точке пласта,
- соответственно текущее давление и насыщенность коллектора флюидом в произвольной точке пласта, ![]() - коэффициент продуктивности скважины, К (p), Fн (
- коэффициент продуктивности скважины, К (p), Fн (![]() ), h (p) — соответственно абсолютная и фазовая проницаемость и действующая толщина пласта,
), h (p) — соответственно абсолютная и фазовая проницаемость и действующая толщина пласта, ![]() - вязкость и плотность флюида.
- вязкость и плотность флюида.
С целью вывода уравнения притока с начальным градиентом давлении формулу (3) преобразуем в следующий вид:
![]()
Здесь v- является скоростью флюида. Для однофазной нефти она имеет вид:
![]() , для двухфазной фильтрации:
, для двухфазной фильтрации:
![]()
Преобразуем данное равенство для однофазной фильтрации в следующий вид:
![]()
Учитывая что ![]() и интегрируя последнее уравнение получим:
и интегрируя последнее уравнение получим:
![]() или
или
![]()
Введя обозначение ![]() из последнего уравнения получаем:
из последнего уравнения получаем:
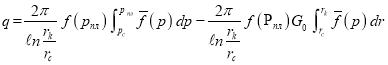 или
или
![]()
где
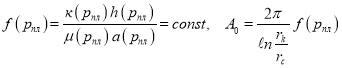
В последнем уравнении представляя![]() получаем:
получаем:
![]() (12)
(12)
Если изменения комплекса параметров происходит по линейному закону, т. е.
![]() , то для дебита притока получаем:
, то для дебита притока получаем: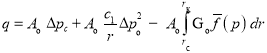 .
.
В последнее уравнение, введя обозначение ![]() , мы получаем,
, мы получаем,
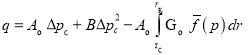 т. е. уравнение (6).
т. е. уравнение (6).
Если мы в качестве закона фильтрации возьмем двучленный закон фильтрации:
![]()
то, проводя аналогичные преобразования, получаем выражение:
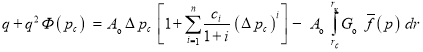 . (13)
. (13)
Здесь
Проводимые исследования показывают, что этот коэффициент при депрессиях порядка 10 МПа может составлять максимум 1015 %.
В полученной формуле (13)
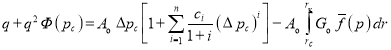
при Gо = 0 (т. е. без начального градиента) мы получаем известную нам формулу. Это показывает, что влияние начального градиента показывает себя только во втором слагаемом. Обозначим ее через q(рo). Тогда при ![]() =0, получаем.
=0, получаем.
![]() , (14)
, (14)
где 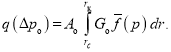 Здесь значение интеграла
Здесь значение интеграла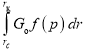 выражается через геометрию пласта (rcи rк) и начальный градиент Gо. При Gо = const применяем для данного интеграла теорему о среднем. Тогда,
выражается через геометрию пласта (rcи rк) и начальный градиент Gо. При Gо = const применяем для данного интеграла теорему о среднем. Тогда,
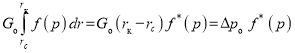
и ![]()
Учитывая последнее выражение в (12), получаем:
![]() (15)
(15)
Для нахождения
q = 0, то из (18):
![]()
или
![]() . (16)
. (16)
Тогда уравнение притока для одиночной скважины примет вид:
![]() (17)
(17)
После несложных преобразований имеем
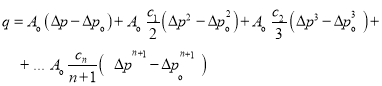 (18)
(18)
Обозначая ![]() , получаем следующее уравнение:
, получаем следующее уравнение:
![]() (19)
(19)
При двучленном законе фильтрации
![]() (20)
(20)
В частных случаях при![]() получается формула Дюпи, при
получается формула Дюпи, при
Аi = ![]() известная двучленная формула, при
известная двучленная формула, при![]() получается уравнения притока, приведенные в для экспоненциальных зависимостей параметров флюида и коллектора от давления при
получается уравнения притока, приведенные в для экспоненциальных зависимостей параметров флюида и коллектора от давления при ![]()
Получается формула (4).
Легко получается и ряд других, встречающихся в литературе формул притока.Для изучения характера изменения коэффициента продуктивности скважин полученную формулу (20) преобразуем в следующих вид:
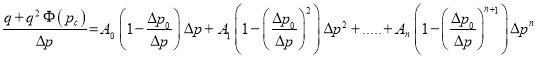 (21)
(21)
Как видно при достаточно больших значения депрессии ![]() аномальные свойства нефти как будто исчезают, то есть асимптотой функции является выражение:
аномальные свойства нефти как будто исчезают, то есть асимптотой функции является выражение:
![]() или
или
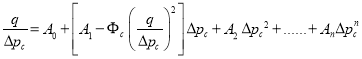
Ф это формула для КПС без начального градиента.
Последняя формула является известная формула которую мы уже рассматривали. При
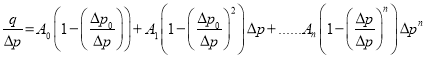 (21)
(21)
Так как здесь ![]() то
то
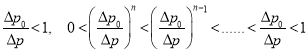
При больших значениях ![]() форма индикаторной линии с начальным значением как бы совпадает с формой индикаторной линии без начального градиента. В связи с этим индикаторные линии могут иметь следующие формы
форма индикаторной линии с начальным значением как бы совпадает с формой индикаторной линии без начального градиента. В связи с этим индикаторные линии могут иметь следующие формы
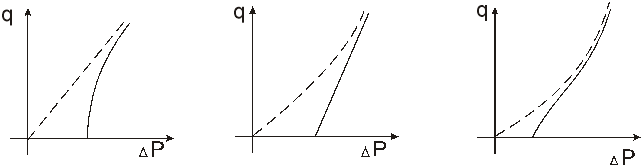
Однофазная фильтрация
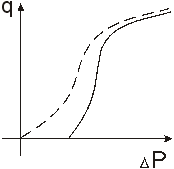
Переход от однофазной к двухфазной
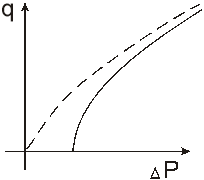
Двухфазная фильтрация
Литература:
- О структурно-механических свойствах нефтей месторождения Котур-Тепе, изв.вуз. «Нефть и газ» № 11, 1969, Ч.Атабаев, Р. Аллахвердиев.
- Ф. Х. Мирзаджанзаде, А. Г. Ковалев, Ю. В. Зайцев. Особенности эксплуатации месторождений аномальных нефтей. М., «Недра», 1972, с.200.
- Горбунов А. Т. Разработка аномальных нефтяных месторождений. М., «Недра», 1981, с.240.
- К. С. Басниев, А. М. Власов и др. Подземная гидравлика. М., «Недра», 1986, с.303.
- М. Т. Абасов, Ч. Т. Атабаев, А. М. Кулиев и др. Методика определения нелинейного эффекта по кривым изменения коэффициента продуктивности скважин от депрессии. Изв.АНАзерб.ССР № 1, 1977, с.7.
- Временное руководство погидродинамическим методом изучения фильтрационных свойств залежи нефти и газа, характеризующихся высокими пластовыми давлениями / М. Т. Абасов, Э. Х. Азимов, А. М. Кулиев, Г. С. Мамиев и др. Баку, Элм, 1978, 128с.
- Э. Х. Азимов, В. Н. Аллахвердиев, Л. М. Билаллы, И. Р. Гасанов. Методика интерпретации индикаторных линий газовых и газоконденсатных скважин. Азербайджанское нефтяное хозяйство, 1987, № 5, с.24–28.







