Key words: complex system, the classification uncertainty of a priori uncertainty, adaptive system
The study of the power system as a control object that allows to build its mathematical model. Using this framework, the type and algorithms of the system of governance and ways of its software and hardware implementation.
To build an adequate mathematical model of the control object requires a large amount of a priori information. This information about controlled and uncontrolled perturbations, internal parameters and status variables of the object, and its output signals. It should be noted that the high dimensionality and complexity of the mathematical model built using the entire volume of a priori information, can negate all attempts of control.
Generally, some of the information about complex object of management and its interaction with the environment is not defined and even unknown. The presence of a variety of interference, which is a source of uncertainty leads to incomplete a priori information.
The essential feature of any a priori information consists in the fact that, being received in advance, they are then not only not updated, but due to various random changes always existing in the real world, lose their accuracy [1].
Uncertainty can be caused by exogenous (determined by external factors) or endogenous factors (determined by internal changes).
To endogenous factors include:
– parametric;
– structural;
– uncertainty.
Parametric uncertainty. Along with the state variables the system is characterized by parameters. The parameters of the system include mass, inductance, capacitance, length, resistance, etc. system Parameters can be partially defined or determined some average values. In the process of functioning of the system they can change.
The structural uncertainty. Modern control systems are characterized by complex hierarchical structure. With the transition from the lower to the upper level system structure is complicated, added the cross and feedback that are sometimes difficult. Wrong decomposition of the control tasks, excessive idealization of a complex process, linearization, discrimination, violation of the assumptions adopted in the derivation of the equations leads to inaccurate models [2, 3].
Mathematical description of systems in terms of apriori uncertainty.
In conditions of a priori uncertainty of traditional principles of building control systems are ineffective. When using the principle of control by deviation small changes in the actual behavior of the control object, in connection with the inability to quickly make adjustments to the management process and lead to unsatisfactory results [4]. When using the principle of compensation for disturbance is necessary to directly measure the disturbance that is often impossible. Using the principle of combined control deviation and disturbance does not always lead to the desired results. Do the drift parameters of the object, the channel delay compensation will negate all attempts to stabilize the object. Using the principle of control as it entails the same problems of management.
It should be noted that these problems can be solved for relatively simple objects of control with parametric uncertainties or uncertainties in the input and output signals. They are described by linear models in the form of input-output, input-state-output or well-studied nonlinear systems of equations. As a mathematical model of a complex system to use them is problematic. This is due not only to the hierarchical structure of complex systems, and, consequently, the presence of several optimality criteria, but also with the presence of structural uncertainties that cannot be eliminated using classical mathematical models and techniques.
Consideration of uncertainty in decision tasks is largely modifies the methods of decision making: the concept of the initial data and the parameters of the model become ambiguous concept of decision tasks and optimality of solutions. Attempts to use a particular mathematical apparatus for decision making under uncertainty allows to adequately reflect in the model, only certain types of data and leads to irrevocable loss of other types of information [5].
These problems can be solved by using the principles of adaptation. Adaptation is the process of changing parameters, structure, input signals of the system on the basis of current information to achieve the control objectives, in conditions of a priori uncertainty and variable conditions.
The a priori uncertainty kompensiruet current information through processes of learning or self learning. The learning process takes place at multiple external influences on the system by fixing its reaction and further external adjustment of management objectives. For the process of self-study external adjustment of the control objectives is missing. Thus, when using the principle of adaptation in the process of learning or self-study there is an accumulation of data which is subsequently used to compensate for uncertainty and management objectives.
To use the principle of adaptation, you need to know: the class of belonging of the object of control, the conditions of its functioning, the purpose of management.
The task is to construct a regulator that is acting on an object that implements the target control after a finite time. In this class the controller will be adaptive, and the system itself is adaptive. The end time of the achievement of the objective will be a time of adaptation. If the conditions of a priori uncertainty the –object belongs to the class of adaptation of the controller, the adaptive controller can be achieved [6].
As shown in [7] the classification adaptive systems are divided into:
– passive — controlled changes to the system software depend on the available at the design stage of a priori information about the internal and external conditions of work;
– active — controlled changes to the system software dependent on current and not just a priori information about the internal and external conditions of work;
– open — setup parameters are pre-determined and so that the control system was estimated optimally in some typical or most probable external and internal conditions;
– closed — have additional closed loop self-tuning, serving for analysis of the effect of changes in the quality management system in the process of adaptation;
– analytical — controlled changes in parameters or input actions made as a result of the analytical calculation of the conditions of extremum of the function that defines the purpose and quality management;
– search controlled parameter changes made as a result of the search for extremum quality.
The classification analysis shows that a complex hierarchical system it is necessary to synthesize the active closed-loop adaptive system with variable structure. Combined method the settings will allow you to achieve high levels of quality system: the first phase, with a sufficient amount of a priori information, an analytical method are determined by controlled changes of the settings and after a short period of time is calculated, the optimal mode; in the second stage search method is determined by the optimal mode.
Statement of the problem of adaptation and stages of its solution. Consider the scheme of interaction of the object of control (![]() ), control (
), control (![]() ) and sensors (
) and sensors (![]() ) (Fig. 1). The influence of the external environment, control actions and internal perturbations is reflected in the change of state of the control object. Status information is measured by sensors and fed into a vector signal to the control device. Based on this information and management purposes, the control device generates control actions.
) (Fig. 1). The influence of the external environment, control actions and internal perturbations is reflected in the change of state of the control object. Status information is measured by sensors and fed into a vector signal to the control device. Based on this information and management purposes, the control device generates control actions.
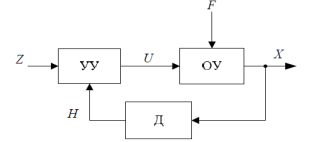
Fig. 1. Scheme closed-loop control system
For the formulation of adaptive management requires the vectors:
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
where ![]() – the vector of varied parameters, which serve not only the real physical quantity but an abstract, for example, the structures of the control object.
– the vector of varied parameters, which serve not only the real physical quantity but an abstract, for example, the structures of the control object.
In the General case, this vector reflected uncertainty.
For example, if the channel measurement is present an obstacle, the set may ![]() consist of the coefficients of its spectral characteristics [5].
consist of the coefficients of its spectral characteristics [5].
Description of adaptive control system can be performed using the equations:
![]() , (1)
, (1)
![]() , (2)
, (2)
where ![]() – indicates a reference not coordinate;
– indicates a reference not coordinate; ![]() – some functions.
– some functions.
In accordance with the terminology adopted in [5] equation (1) is called the sensory equation, and the equation (2) — evolutionary. If a mathematical model of the control object is unknown, for the operation of the adaptive controller needs only the coordinates of the vector ![]() .
.
The objective of control ![]() is usually reflected in the form of some optimality criterion. As the criteria of optimality can be [8] the following criteria.
is usually reflected in the form of some optimality criterion. As the criteria of optimality can be [8] the following criteria.
- Criteria-inequality
- Criteria-equality
![]() .
.
- The minimization criteria
![]() .
.
Thus, the goal of adaptation is to solve the problem
![]() ,
,
where ![]() –the desired management goal.
–the desired management goal.
The solution of the problem of synthesis of adaptive controller is performed in stages:
– the choice of the structure of the regulator: it is necessary to determine the structure of the regulator, which will implement goals of management;
– the selection of adjustable parameters: you must allocate physical and abstract parameters or evaluation;
– adaptive algorithm: it is necessary to synthesize an adaptation algorithm, performing adjustment of parameters;
– justification of the adaptation algorithm: it is necessary to prove that the synthesized system is adaptive.
References:
- Tsypkin Y. Z. Information theory of identification. — M.: Science. Fizmatlit, 1995. — 336 p.
- Tsypkin, Ya. z., Frequency criteria of robust modal linear discrete systems / Ya. z. Tsypkin, B. T. Polyak // Automation.-1990. — No. 5. — P. 4–11.
- Tsypkin, Y. Z. Robust stability of nonlinear discrete systems with parametric uncertainty / Y. Z. Tsypkin // Automation.-1992.- No. 4.- C. 3–9.
- Emelyanov S. V., Korovin S. K. New types of feedback: Management under uncertainty. — M.: Science. Fizmatlit, 1997. — 352 p.
- Altunin A. E., semuhin M. V. Models and algorithms of decision making in fuzzy environment: Monograph. — Tyumen: Publishing house Tyumen state University, 2000. — 352 p.
- Fomin V. N., Fradkov A. L., Yakubovich V. A. Adaptive control of dynamic objects. — M.: Science. Home edition physical and mathematical literature, 1981. — 448 p
- Solodovnikov V. V., Plotnikov V. N., Yakovlev A. V. on the Theory of automatic control of technical systems: Textbook. allowance. — M.: Izd-vo MGTU, 1993.– 492 p.
- Rastrigin L. A. Adaptation of complex systems. — Riga: Zinatne, 1981. — 375 S. Solovyev, Victor V.







