Введение
Среди монографий и статей, посвящённых построению и развитию теории поиска объектов, можно выделить ряд основных, например, [1] – [5]. Центральным вопросом в этих работах является выбор моделей поисковых усилий (поискового потенциала) поисковой системы и поисковых единиц, её составляющих. С одной стороны эти модели должны быть достаточно обобщёнными для построения общей теории поиска объектов, а с другой стороны отражать особенности средств наблюдения, которыми оснащены поисковые единицы, для получения возможности формирования оптимального управления ими. Дополнительным ограничением, влияющим на вид моделей поисковых усилий, является необходимость их согласованности с используемым для оптимизации критериальным показателем эффективности процесса поиска. Требованиям наибольшей общности и согласованности с вероятностными критериями поиска удовлетворяет модель для пуассоновского потока обнаружений, определяемая интенсивностью поиска [1]. Например, в ряде работ ([2], [4], [5]) поисковое усилие в точке z за время 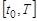 определяется как функция вида
определяется как функция вида 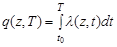 , где
, где 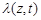 – интенсивность потока обнаружений (в терминах теории марковских случайных процессов – плотность потока событий), получившая название функции плотности поисковых усилий (функции плотности поиска) ([2], [4], [5]), интенсивности поиска ([1], с. 14) или стратегии поиска ([2], с. 8) . При этом, в монографии В.А. Абчука и В.Г. Суздаля [1] функция
– интенсивность потока обнаружений (в терминах теории марковских случайных процессов – плотность потока событий), получившая название функции плотности поисковых усилий (функции плотности поиска) ([2], [4], [5]), интенсивности поиска ([1], с. 14) или стратегии поиска ([2], с. 8) . При этом, в монографии В.А. Абчука и В.Г. Суздаля [1] функция 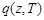 названа поисковым потенциалом, а в статье В.И. Аркина [4] ещё имеет энергетическую трактовку, как плотность энергии, пришедшейся на точку z во время рассматриваемого интервала времени. Наиболее общая теория поиска, построенная в монографии О. Хеллмана, решает проблему оптимизации поискового усилия
названа поисковым потенциалом, а в статье В.И. Аркина [4] ещё имеет энергетическую трактовку, как плотность энергии, пришедшейся на точку z во время рассматриваемого интервала времени. Наиболее общая теория поиска, построенная в монографии О. Хеллмана, решает проблему оптимизации поискового усилия 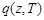 на основе синтеза стратегии поиска
на основе синтеза стратегии поиска 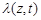 и даёт «только некоторое математическое выражение, заданное в области поиска» ([1], с. 66). Там же отмечается, «что трудная практическая проблема заключается в том, чтобы расположить средства поиска таким образом, чтобы поисковое усилие было близко к оптимальному, насколько это возможно. Достаточно очевидно, что никакая математическая форма поискового усилия
и даёт «только некоторое математическое выражение, заданное в области поиска» ([1], с. 66). Там же отмечается, «что трудная практическая проблема заключается в том, чтобы расположить средства поиска таким образом, чтобы поисковое усилие было близко к оптимальному, насколько это возможно. Достаточно очевидно, что никакая математическая форма поискового усилия 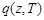 в этом случае не будет в точности воспроизводиться некоторой реальной системой поиска».
в этом случае не будет в точности воспроизводиться некоторой реальной системой поиска».
С другой стороны хорошо отработаны практические вопросы радиолокационного поиска целей. Процесс поиска в таких системах основывается на радиолокационном обзоре – периодическом облучении всех точек заданной области пространства и приёме сигналов тех целей, которые находятся в этой области [6]. Здесь рассматриваются постановки задач поиска по жёсткой программе и адаптивного поиска [6], [7]. Достоинства поиска по жёсткой программе заключается в простоте реализации, однако его недостаток состоит в нерациональном распределении поисковых усилий, что сопряжено со значительными временными затратами на его осуществление. Этого недостатка лишён адаптивный поиск. Адаптация поиска может базироваться на комплексном использовании всех возможных видов априорной информации [7] (о характеристиках потока целей; о пространственно-временном распределении целей в реальном масштабе времени), полученной как от внешних источников, так и в процессе функционирования самой радиолокационной системы.
Существует ряд вариантов построения адаптивного поиска. Однако все они разработаны для одиночных средств поиска, основаны на эвристических алгоритмах с оптимизацией по одному или нескольким параметрам, и, как правило, не учитывают динамику искомого объекта.
Построенный в работах [8] – [10] траекторный подход обладает достаточной общностью и позволяет учитывать управление отдельными поисковыми единицами, однако рассмотрен только для задач поиска объектов многопозиционными поисковыми системами с неподвижными поисковыми единицами (измерительно-поисковыми пунктами). Кроме того, не рассмотрен случай объединения поисковых единиц в группы с формированием общих поисковых усилий этих групп, который становится актуальным, например, для многопозиционных радиолокационных систем, когда измеряемыми параметрами являются разности или суммы дальностей.
Модель поисковых усилий для решения оптимизационных задач по поиску управления отдельными поисковыми единицами и их группами в составе поисковой системы, должна отражать зависимость функции 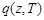 от ряда параметров управления. К ним следует отнести параметры управления самих поисковых единиц, их групп и средств наблюдения, которыми оснащены поисковые единицы. Совокупность таких управляющих параметров, заданных на определённом временном интервале представляет план поиска на этом временном интервале. Ясно, что вид функции поисковых усилий от управляющих параметров средств наблюдения существенно зависит от того, какие средства наблюдения применяются. Однако, при определённой классификации, такие функции могут быть унифицированы для соответствующих классов отдельных средств наблюдения и средств наблюдения, которыми оснащена группа поисковых единиц. В качестве общего классификационного признака можно рассматривать вид поверхности положения. При этом под поверхностью положения понимается (как и, например, в радиотехнических системах) геометрическое место точек, для которых измеряемый параметр инвариантен.
от ряда параметров управления. К ним следует отнести параметры управления самих поисковых единиц, их групп и средств наблюдения, которыми оснащены поисковые единицы. Совокупность таких управляющих параметров, заданных на определённом временном интервале представляет план поиска на этом временном интервале. Ясно, что вид функции поисковых усилий от управляющих параметров средств наблюдения существенно зависит от того, какие средства наблюдения применяются. Однако, при определённой классификации, такие функции могут быть унифицированы для соответствующих классов отдельных средств наблюдения и средств наблюдения, которыми оснащена группа поисковых единиц. В качестве общего классификационного признака можно рассматривать вид поверхности положения. При этом под поверхностью положения понимается (как и, например, в радиотехнических системах) геометрическое место точек, для которых измеряемый параметр инвариантен.
Рассмотрим ситуацию объединения поисковых единиц в группы с формированием из расположенных на них средств наблюдения единых каналов поиска групп, поверхность положения которых является в пространстве поиска гиперболоидом и эллипсоидом. Такие средства наблюдения (каналы поиска) будем называть гиперболоидными и эллипсоидными. Примерами таких средств наблюдения являются широко применяемые разностно-дальномерные и суммарно-дальномерные измерительные системы.
Таким образом, задача построения и обоснования математической модели поисковых усилий системы, состоящей из групп поисковых единиц (в общем случае не являющихся неподвижными), с гиперболоидными и эллипсоидными каналами поиска, является актуальной.
Постановка задачи
Пусть задано некоторое 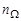 - мерное нормированное пространство поиска
- мерное нормированное пространство поиска 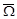 с нормой
с нормой 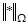 . В пространстве
. В пространстве 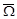 определена область поиска
определена область поиска 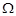 (т.е.
(т.е. 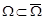 , при этом здесь и далее множество элементов пространства будем обозначать тем же символом, что и само пространство).
, при этом здесь и далее множество элементов пространства будем обозначать тем же символом, что и само пространство).
Будем полагать, что поисковая система является групповой, т.е. состоит из нескольких поисковых единиц. При этом каждая поисковая единица оснащена одним сферическим средством наблюдения (т.е. средством наблюдения, поверхностью положения которого является сфера). Без ограничения общности полагаем, что поисковая система (ПС) включает J поисковых единиц (ПЕ), динамика векторов состояния которых в пространстве 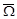 описывается непрерывным марковским процессом, модель которого имеет вид:
описывается непрерывным марковским процессом, модель которого имеет вид:
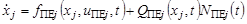 ,
, 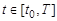 ,
, 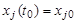 ,
, 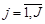 , (1)
, (1)
где 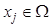 ,
, 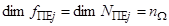 ,
,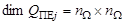 ,
, 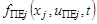 – заданные функции,
– заданные функции, 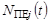 – векторы формирующих шумов,
– векторы формирующих шумов, 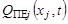 – матрицы интенсивностей,
– матрицы интенсивностей, 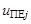 – вектор управления состоянием j-ой поисковой единицы в пространстве
– вектор управления состоянием j-ой поисковой единицы в пространстве 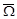 ,
, 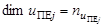 ,
, 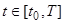 .
.
Пространство состояний ПЕ, как правило, имеет большую размерность по сравнению с пространством 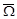 . Однако для рассматриваемой задачи построения математической модели поисковых усилий это обстоятельство не является принципиальным, поэтому для упрощения записей положим, что эти пространства совпадают.
. Однако для рассматриваемой задачи построения математической модели поисковых усилий это обстоятельство не является принципиальным, поэтому для упрощения записей положим, что эти пространства совпадают.
Будем полагать, что первые 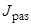 (
(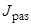 – чётное число) из J поисковых единиц образуют попарно группы с формированием гиперболоидных каналов поиска (число групп
– чётное число) из J поисковых единиц образуют попарно группы с формированием гиперболоидных каналов поиска (число групп 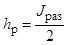 ), следующие
), следующие 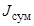 (
(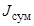 – чётное число) – группы с формированием эллипсоидных каналов поиска (число групп
– чётное число) – группы с формированием эллипсоидных каналов поиска (число групп 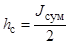 ), а остальные (
), а остальные (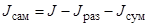 ) поисковые единицы являются самостоятельными.
) поисковые единицы являются самостоятельными.
Положение каждого k-го (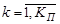 ) нового объекта поиска (ОП) в области
) нового объекта поиска (ОП) в области 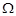 задаётся начальной плотностью распределения
задаётся начальной плотностью распределения 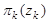 ,
, 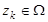 . Их динамика в пространстве состояний объектов поиска
. Их динамика в пространстве состояний объектов поиска  описывается непрерывным марковским процессом, модель которого имеет вид:
описывается непрерывным марковским процессом, модель которого имеет вид:
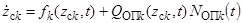 , (2)
, (2)
где 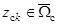 ,
, 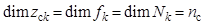 ,
, 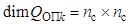 ,
, 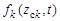 – заданные функции,
– заданные функции, 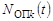 – векторы формирующих шумов,
– векторы формирующих шумов, 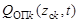 – матрицы интенсивностей,
– матрицы интенсивностей, 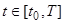 . В общем случае
. В общем случае 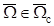 . Обоснованность применения моделей (1), (2) рассмотрена, например, в [11].
. Обоснованность применения моделей (1), (2) рассмотрена, например, в [11].
Полагается, что области поиска 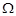 , динамика целей и начальные плотности распределения положения целей
, динамика целей и начальные плотности распределения положения целей 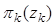 ,
, 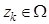 таковы, что
таковы, что
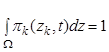 (3)
(3)
для всех 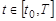 .
.
Без ограничения общности рассмотрим ситуацию, когда все поисковые единицы оснащены непрерывными средствами наблюдения.
В целях формулирования постановки задачи по определению модели поисковых усилий введём обозначения. Пусть
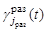 – функции, определяющие режим функционирования средств наблюдения поисковых единиц, входящих в
– функции, определяющие режим функционирования средств наблюдения поисковых единиц, входящих в 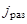 -ю группу со средствами наблюдения, образующими гиперболоидный канал поиска (
-ю группу со средствами наблюдения, образующими гиперболоидный канал поиска (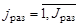 ),
), 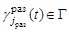 ,
, 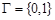 ,
,
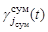 – функции, определяющие режим функционирования средств наблюдения поисковых единиц, входящих в
– функции, определяющие режим функционирования средств наблюдения поисковых единиц, входящих в 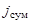 -ю группу со средствами наблюдения, образующую эллипсоидный канал поиска (
-ю группу со средствами наблюдения, образующую эллипсоидный канал поиска (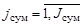 ),
), 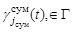 ,
,
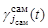 – функции, определяющие режим функционирования средств наблюдения самостоятельных поисковых единиц, образующих сферические каналы поиска (
– функции, определяющие режим функционирования средств наблюдения самостоятельных поисковых единиц, образующих сферические каналы поиска (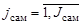 ),
), 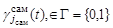 ,
,
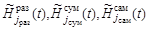 и
и 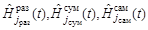 – функции, определяющие функционирование соответствующих каналов поиска, и их допустимые множества.
– функции, определяющие функционирование соответствующих каналов поиска, и их допустимые множества.
Тогда ограничения, учитываемые в процессе поиска, формируются на основе выражений:
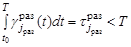 ,
, 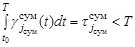 ,
, 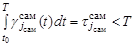 , (4)
, (4)
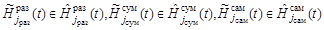 ,
, 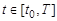 . (5)
. (5)
Если функционал W определяет один из возможных вероятностных критериев эффективности процесса поиска динамических объектов на интервале времени 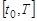 , то задачу оптимального управления поиском динамических объектов можно сформулировать в следующем виде:
, то задачу оптимального управления поиском динамических объектов можно сформулировать в следующем виде:
найти план функционирования ПС
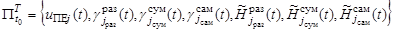 , (6)
, (6)
где 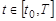 ,
, 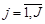 ,
,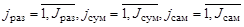 ,
,
обеспечивающий экстремум функционала
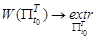 , (7)
, (7)
в условиях ограничений (1) – (5) .
Для задачи (1) – (7) требуется построить математическую модель поисковых усилий 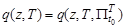 .
.
Построение математической модели поисковых усилий системы с группами поисковых единиц
Реальные объекты, которые участвуют в процессе поиска (и, следовательно, сам этот процесс) обладают множеством свойств и характеризуются бесконечным множеством связей как внутри объектов, так и связями с другими объектами и окружающей средой. Переход к их моделям является наиболее сложным и ответственным этапом применения математического аппарата для решения задач анализа и синтеза структур и алгоритмов функционирования поисковых систем. В значительной мере успешное решение этих задач определяется субъективными факторами [12]. В то же время можно указать и ряд общих требований, которые обычно предъявляются к математической модели: достаточная точность, предельная простота и стандартная форма. Обеспечение достаточной точности основано на учёте всех существенных свойств и связей, отвлекаясь от второстепенных, несущественных свойств [12]. Решение этого вопроса зависит не только от характера самого объекта, модель которого строится, но и от поставленной задачи.
На основе анализа процесса поиска, объектов, которые в нём задействованы, и поставленной задачи можно сформулировать следующие обязательные требования к модели поисковых усилий. Математическая модель поисковых усилий групповой поисковой системы должна:
– характеризовать накопленную за интервал времени суммарную информацию об энергетических отношениях сигнал-шум на входах средств наблюдения, соответствующих заданной точке области поиска;
– позволять определить заданный показатель эффективности поиска;
– включать управляемые переменные, влияющие на значение заданного показателя эффективности поиска;
– обладать свойством аддитивности относительно поисковых усилий отдельных поисковых единиц (средств наблюдения);
– обладать достаточной общностью, чтобы позволять описывать различные средства наблюдения.
В соответствии с первым рассмотренным требованием и на основе траекторного подхода к описанию поисковых усилий [8] – [10], представим поисковое усилие по поиску k-го ОП для заданной точки z области поиска в следующем виде:
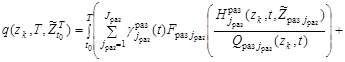
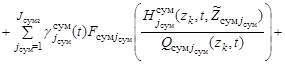
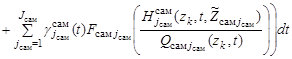 , (8)
, (8)
где 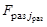 ,
, 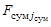 ,
, 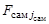 – функции, характеризующие плотности поисковых усилий соответствующих каналов поиска,
– функции, характеризующие плотности поисковых усилий соответствующих каналов поиска, 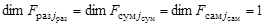 ,
, 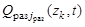 ,
, 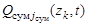 ,
, 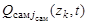 – функции, характеризующие интенсивность шумов в соответствующих каналах поиска,
– функции, характеризующие интенсивность шумов в соответствующих каналах поиска, 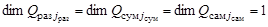 ,
, 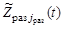 ,
, 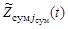 ,
, 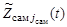 – траектории поиска соответствующих средств наблюдения [8] – [10], которые являются одними из управляемых переменных, влияющих на значение заданного показателя эффективности поиска,
– траектории поиска соответствующих средств наблюдения [8] – [10], которые являются одними из управляемых переменных, влияющих на значение заданного показателя эффективности поиска, 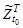 – обозначение совокупности траекторий поиска
– обозначение совокупности траекторий поиска 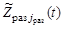 ,
, 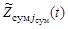 ,
, 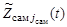 при
при 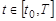 ,
, 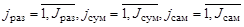 ,
, 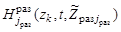 ,
, 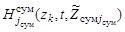 ,
, 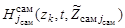 – «сигнальные» функции соответствующих каналов поиска,
– «сигнальные» функции соответствующих каналов поиска, 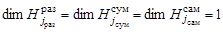 . При этом функции
. При этом функции 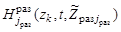 ,
, 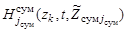 ,
, 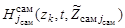 имеют следующие свойства:
имеют следующие свойства:
1. При 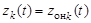 и
и 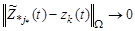 (где
(где 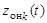 – вектор действительного состояния ОН в пространстве
– вектор действительного состояния ОН в пространстве 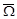 ,
, 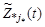 – обозначение
– обозначение 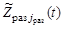 ,
, 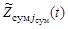 ,
, 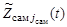 ) функции
) функции 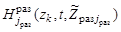 ,
, 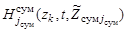 ,
, 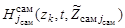 должны возвращать значения измеряемых параметров. Или иначе,
должны возвращать значения измеряемых параметров. Или иначе, 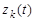 соответствует максимальное значение энергетического отношения сигнал-шум.
соответствует максимальное значение энергетического отношения сигнал-шум.
2. При 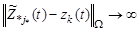 значения
значения 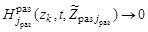 ,
, 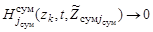 ,
, 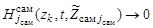 тем самым, характеризуя отсутствие цели в элементе разрешения по измеряемым параметрам. Или иначе, на
тем самым, характеризуя отсутствие цели в элементе разрешения по измеряемым параметрам. Или иначе, на 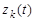 приходится минимальное значение энергетического отношения сигнал-шум.
приходится минимальное значение энергетического отношения сигнал-шум.
3. При промежуточных значениях 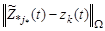 эти функции задают распределение энергетического отношения сигнал-шум в области поиска и, таким образом, характеризуют как значение измеряемых параметров, так и степень возможности его получения в зависимости от
эти функции задают распределение энергетического отношения сигнал-шум в области поиска и, таким образом, характеризуют как значение измеряемых параметров, так и степень возможности его получения в зависимости от 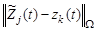 .
.
Отметим, что модель соответствует требованию аддитивности относительно поисковых усилий отдельных поисковых единиц (средств наблюдения), т.е.
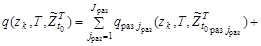
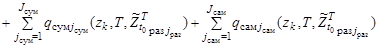 , (9)
, (9)
где 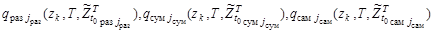 – поисковые усилия соответствующих групп и самостоятельных поисковых единиц,
– поисковые усилия соответствующих групп и самостоятельных поисковых единиц, 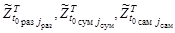 – обозначение реализаций траекторий поиска на интервале
– обозначение реализаций траекторий поиска на интервале 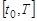 соответствующих каналов поиска,
соответствующих каналов поиска,
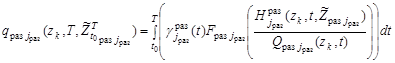 , (10)
, (10)
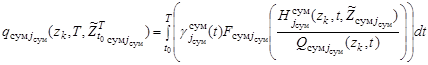 , (11)
, (11)
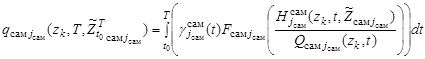 . (12)
. (12)
Рассмотрим возможные формы представления функций 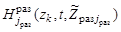 ,
, 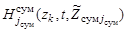 ,
, 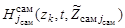 . Положим, что они для удовлетворения указанным свойствам представляют собой произведение значений измеряемых параметров
. Положим, что они для удовлетворения указанным свойствам представляют собой произведение значений измеряемых параметров 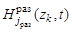 ,
, 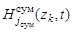 ,
, 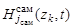 , выраженных через вектор координат рассматриваемой точки
, выраженных через вектор координат рассматриваемой точки 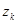 пространства
пространства 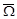 , и функций, характеризующих степень возможности получения этих значений при траекториях поиска
, и функций, характеризующих степень возможности получения этих значений при траекториях поиска 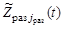 ,
, 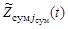 ,
, 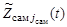 –
– 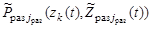 ,
, 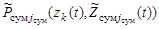 ,
, 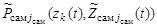 соответственно, отражающих методические особенности формирования измеряемых параметров.
соответственно, отражающих методические особенности формирования измеряемых параметров.
Поскольку рассматривается задача построения для пространства 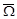 математическую модель поисковых усилий
математическую модель поисковых усилий 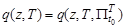 поисковой системы, состоящей из групп и самостоятельных поисковых единиц, формирующих гиперболоидные, эллипсоидные и сферические каналы поиска, то функции
поисковой системы, состоящей из групп и самостоятельных поисковых единиц, формирующих гиперболоидные, эллипсоидные и сферические каналы поиска, то функции 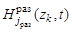 ,
, 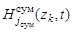 ,
, 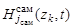 принимают вид:
принимают вид:
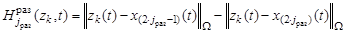 , (13)
, (13)
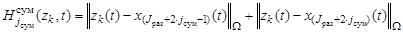 , (14)
, (14)
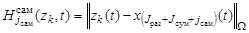 . (15)
. (15)
В свою очередь, функции 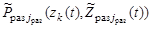 ,
, 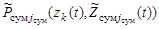 ,
, 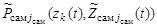 для пространства
для пространства 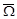 по определению могут быть представлены в виде:
по определению могут быть представлены в виде:
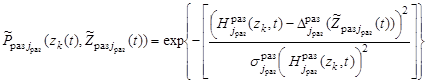 , (16)
, (16)
где 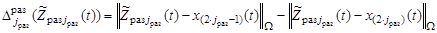 ,
,
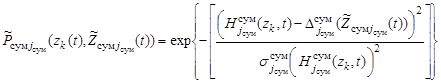 , (17)
, (17)
где 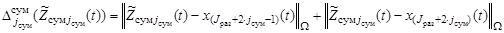 ,
,
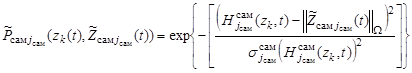 , (18)
, (18)
где 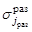 ,
, 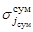 и
и 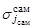 – постоянные величины модели поисковых усилий, характеризующие размеры элементов разрешения соответствующих каналов наблюдения.
– постоянные величины модели поисковых усилий, характеризующие размеры элементов разрешения соответствующих каналов наблюдения.
Подставляя (13) – (18) в (8) получим выражение для определения поискового усилия
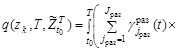
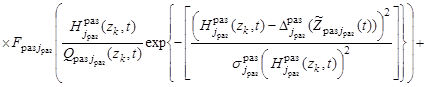
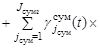
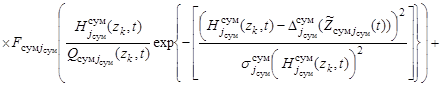
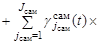
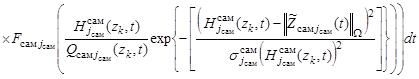 . (19)
. (19)
Покажем, что на основе модели поисковых усилий вида (19) можно определить вероятностные показатели эффективности поиска.
При поиске одиночного ОП поисковой системой, состоящей из нескольких поисковых единиц, наибольшее распространение в качестве показателя эффективности его проведения получила вероятность обнаружения ОП хотя бы одной поисковой единицей, которая для рассматриваемых условий поиска для точки z пространства поиска принимает вид:
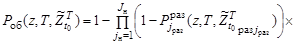
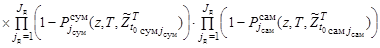 , (20)
, (20)
где 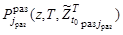 ,
, 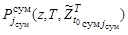 ,
, 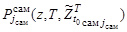 для нестационарного пуассоновского потока обнаружений согласно [1] являются функциями поисковых усилий
для нестационарного пуассоновского потока обнаружений согласно [1] являются функциями поисковых усилий 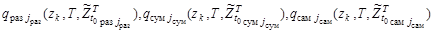 соответствующих каналов наблюдения:
соответствующих каналов наблюдения:
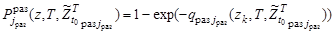 , (21)
, (21)
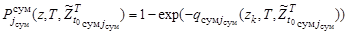 , (22)
, (22)
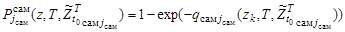 . (23)
. (23)
Но тогда, подставляя выражения (21) – (23) в (20) с учётом (19), можно выразить 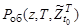 через поисковое усилие поисковой системы, включающей группы поисковых единиц
через поисковое усилие поисковой системы, включающей группы поисковых единиц 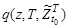 :
:
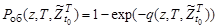 .
.
С другой стороны, вероятность обнаружения единичного ОП в области поиска 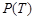 является функцией
является функцией 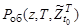 , вид которой определяется условиями поиска. Вопросы построения выражений для этой вероятности для различных условий рассмотрены, например, в [1] – [10].
, вид которой определяется условиями поиска. Вопросы построения выражений для этой вероятности для различных условий рассмотрены, например, в [1] – [10].
При поиске нескольких ОП число возможных вероятностных критериев эффективности поиска возрастает. Это может быть, например, математическое ожидание числа обнаруженных ОП к заданному сроку [1], математическое ожидание времени, необходимого для обнаружения хотя бы одного объекта [1], взвешенная сумма вероятностей их обнаружения в области поиска [10]. Все эти показатели определяются на основе выражений вида (20) – (23). При этом управляемыми переменными модели поисковых усилий, влияющими на значение заданного показателя эффективности поиска (т.е. элементами плана поиска (6)) помимо функций 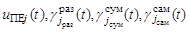 являются траектории поиска соответствующих средств наблюдения (
являются траектории поиска соответствующих средств наблюдения (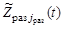 ,
, 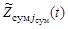 ,
, 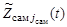 ,
, 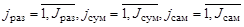 ), являющиеся одним из возможных вариантов представления функций
), являющиеся одним из возможных вариантов представления функций 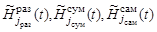 (
(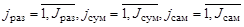 ). В случае отсутствия дополнительных ограничений на траектории поиска, множества
). В случае отсутствия дополнительных ограничений на траектории поиска, множества 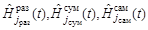 (
(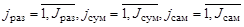 ) совпадают с областью поиска
) совпадают с областью поиска 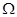 .
.
Таким образом, построенная математическая модель поисковых усилий поисковой системы, состоящей из групп поисковых единиц, оснащённых сферическими средствами наблюдения, образующим различные каналы поиска, удовлетворяет всем поставленным требованиям.
Заключение
Предложенная модель поисковых усилий обобщает модели, полученные в [8] – [10], для множества средств наблюдения, заданного характеристическим свойством, определяемым видом поверхности положения, как на случай подвижных поисковых единиц, так и по размерности пространства, в котором осуществляется поиск.
Библиографический список
- Абчук В.А., Суздаль В.Г. Поиск объектов. М., 1977. 336 с.
- Хеллман О. Введение в теорию оптимального поиска. М., 1985. 248 с.
- Ким Д.П. Методы поиска и преследования подвижных объектов. М., 1989. 336 с.
- Аркин В.И. Задача оптимального распределения поисковых усилий // Теория вероятностей и её применения. 1964. Т. 9. № 1. С. 179–180.
- Аркин В.И. Равномерно-оптимальные стратегии в задачах поиска // Теория вероятностей и её применения. 1964. Т. 9. № 4. С. 746–753.
- Васин В.В. Справочник-задачник по радиолокации. М., 1977. 320 с.
- Шишов Ю.А., Ворошилов В.А. Многоканальная радиолокация с временным разделением каналов. М., 1987. 144 с.
- Строцев А.А. Критерий максимума апостериорной вероятности обнаружения цели к заданному времени // Известия вузов. Радиоэлектроника. 2002. Т.45. № 10. С. 34–41.
- Строцев А.А. Совместное оптимальное управление поиском и наблюдением за условно детерминированными динамическими объектами в импульсной многоканальной измерительно-поисковой системе // Известия вузов. Радиоэлектроника. 2004. Т.47. № 9. С.22–29.
- Строцев А.А., Иващенко И.Л. Синтез оптимального управления многопозиционной информационной системой при поиске группы динамических объектов // Изв. вузов. Радиоэлектроника. 2005. Т. 48. № 10. С. 37–45.
- Школьный Е.П., Майборода Л.А. Атмосфера и управление движением летательных аппаратов. — Л., 1973. 308 с.
- Сигорский В.П. Математический аппарат инженера. Киев., 1975. 768 с.







