Предпрогнозный анализ временных рядов финансовых данных на основе методов фрактального анализа

В статье рассматривается схема применения методов фрактального анализа для выявления фундаментальных характеристик временных рядов финансовых данных, базовым элементом которой является алгоритм R/S-анализа. В соответствии с данным алгоритмом в среде программирования Borland Delphi 7.0 разработан программный продукт, позволяющий выявить и численно оценить фундаментальные характеристики временных рядов, такие как наличие и глубину долговременной памяти, трендоустойчивость (персистентность) или антиперсистентность и др.

 

Фрактальный анализ является новым методом для описания эволюционных процессов и прогнозирования экономических временных рядов. Базовым инструментом для фрактального анализа временных рядов является алгоритм R/S-анализа. Методология R/S-анализа была разработана в середине XX–го века гидрологом Херстом в процессе исследования временных рядов объемов стока рек. В результате проверки предположения о том, что данные ряды подчиняются нормальному закону, Херст определил новую статистику – показатель Херcта (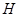). В процессе своих исследований Херст измерял колебания воды в резервуаре относительно среднего с течением времени и ввел безразмерное отношение посредствам деления размаха  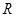на стандартное отклонение наблюдений 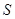. Этот способ анализа стал называться методом нормированного размаха (R/S-анализа). Херст показал, что большинство естественных явлений, включая речные стоки, температуры, осадки, солнечные пятна следует «смещенному случайному блужданию» – тренду с шумом. Сила тренда и уровень шума могут быть оценены тем, как изменяется нормированный размах со временем, или, другими словами, на сколько величина  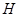превосходит 0,5.

Приведем описание алгоритма R/S–анализа в том виде, как он реализуется в современных методах фрактального анализа [1,2,4]. Пусть дан временной ряд:

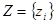
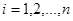 ,                                                            (1)

в котором последовательно выделяем его начальные отрезки:

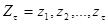, где ,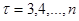

для каждого из которых вычисляем текущее среднее:

.

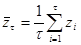Далее для каждого фиксированного 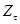,  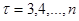вычисляем накопленное отклонение для его отрезков длины :

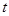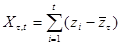, где .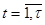

После этого вычисляем разность между максимальным и минимальным накопленными отклонениями:

                                                      ,

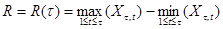которую принято называть термином «размах 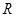». Этот размах нормируется, т.е. представляется в виде дроби 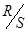, где 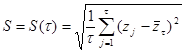 - стандартное отклонение для отрезка временного ряда , .

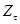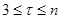Показатель Херста 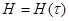, характеризующий фрактальную размерность рассматриваемого временного ряда и соответствующий ему цвет шума, получаем из соотношения  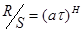[1].

Логарифмируя обе части этого равенства и полагая 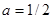 [3], получаем декартовы координаты 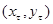, точек 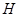–траектории, ординаты и абсциссы которых соответственно равны:

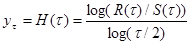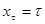,                                  (2)

Требуемая для фрактального анализа ряда (1) R/S-траектория представляется в декартовых логарифмических координатах последовательностью точек, абсциссы которых 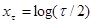, а ординаты .

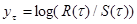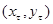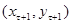Соединяя отрезком соседние точки , и , где 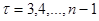, получаем графическое представление R/S-траектории (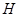-траектории) в логарифмических координатах (в обычных декартовых координатах).

Одной из основных фрактальных характеристик временного ряда является цвет шума, который соответствует этому ряду на том или другом временном отрезке.

Значения 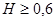 определяют собой черный цвет шума. Чем больше значение 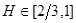, тем большая трендоустойчивость присуща соответствующему отрезку временного ряда.

Значения 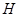 в окрестности  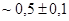определяют собой область белого шума, который соответствует «хаотичному поведению временного ряда» и, следовательно, наименьшей надежности прогноза.

Значения H в окрестности 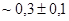 определяют собой область розового шума. Розовый шум говорит о присущей рассматриваемому отрезку временного ряда антиперсистентности [1], это означает, что временной ряд реверсирует чаще, чем ряд случайный (частый возврат к среднему [1]).

Как будет показано ниже, рассматриваемым в настоящей работе рядам присущи черный и, нестрого говоря, «серый шум», соответствующий области нечеткого разграничения между областями черного и белого шумов.

Относительно наличия долговременной памяти рассматриваемого временного ряда (1) не представляется возможным дать положительное или отрицательное заключение, если его 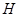–траектория не находится продолжительное время в области черного шума, а поведение R/S-траектории носит хаотичный характер, начиная с ее начальных точек.

Основанием для утверждения о том, что временной ряд (1) обладает долговременной памятью является выполнение следующих условий:

1. 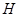      –траектория через несколько своих начальных точек оказывается в области черного шума, а для R/S-траектории указанные точки вхождения в черный шум демонстрируют собой наличие тренда. Глубину этой памяти определяет номер 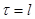, для которого выполняется следующее условие: в точке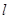 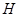 –траектория получает отрицательное приращение, R/S-траектория, в этой точке демонстрирует так называемый «срыв с тренда», т.е. резкое изменение тренда.

2.      Если в данном временном ряде случайным образом перетасовать его элементы и полученный ряд представить на вход алгоритма R/S-анализа, то на выходе алгоритма максимальное значение показателя Херста и R/S-траектории окажется значительно меньше, по сравнению со значениями 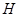 для исходного временного ряда, в случае если этот временной ряд обладает долговременной памятью.

В данной работе R/S-анализу были подвергнуты следующие временные ряды (таблица 1):

 

Таблица 1: Анализируемые временные ряды

 

Анализировались данные по котировкам акций и облигаций Российских эмитентов на Московской Межбанковской Валютной Бирже (ММВБ), индекс ММВБ, отражающий совокупную стоимость акций крупнейших Российских эмитентов, а также курс доллара США по отношению к рублю РФ, устанавливаемый ЦБ РФ.

Используемые в работе временные ряды являются последовательной выборкой (объема 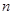) за период с 15 июня 2004 года по 15 июня 2008 года из рыночной статистики, доступной на сайте http://www.quote.ru/. Каждый элемент временного ряда соответствует результату торгов по данному финансовому инструменту за один торговый день.

Для каждого временного ряда 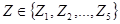 проведен последовательный R/S-анализ, в результате которого для каждого из последовательных отрезков временного ряда  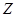длины 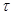 вычислен показатель Херста (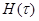), построены 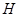–траектория и R/S-траектория соответствующего временного ряда.

На рисунках 1-5 изображены, полученные на выходе R/S-анализа, 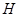 и R/S – траектории для соответствующих временных рядов. Для графиков 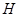–траектории по оси абсцисс отложены длины отрезков ряда 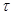. Для графиков R/S-траектории по оси абсцисс отложены величины .

 

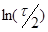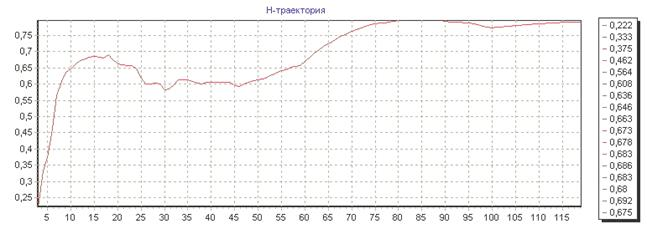
Рис.1(а): 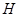–траектория временного ряда

 

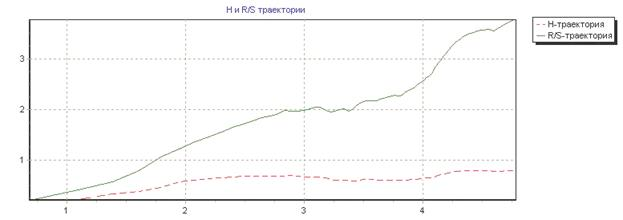
Рис.1(б): R/S-траектория временного ряда

 

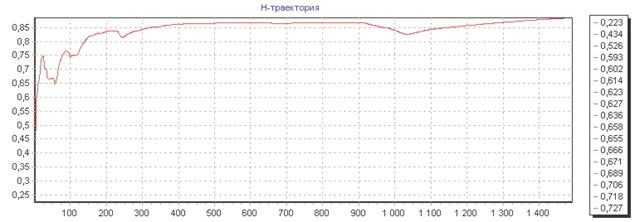
Рис.2(а): 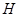–траектория временного ряда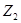

 

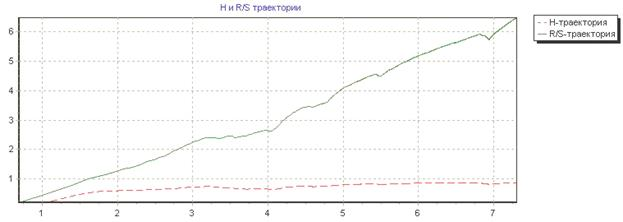
Рис.2(б): R/S-траектория временного ряда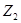

 

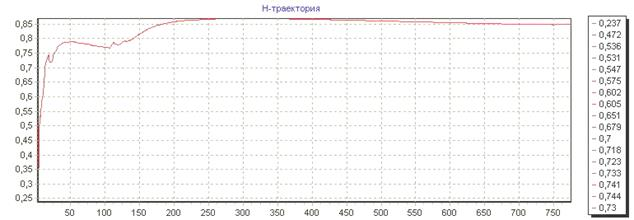
Рис.3(а): 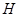–траектория временного ряда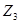

 

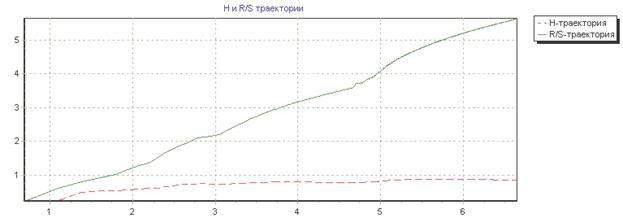
Рис.3(б): R/S-траектория временного ряда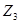

 

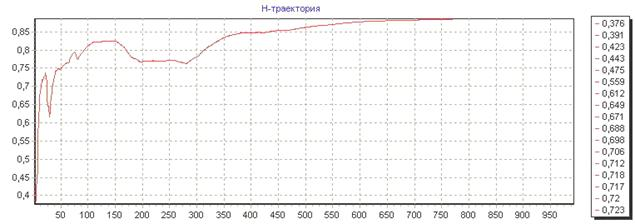
Рис.4(а): 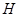–траектория временного ряда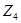

 

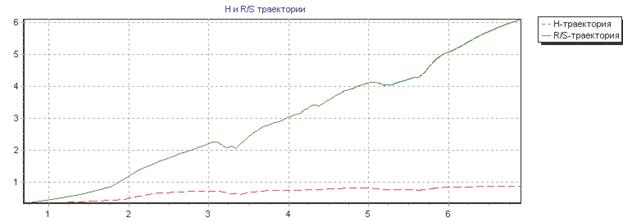
Рис.4(б): R/S-траектория временного ряда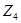

 

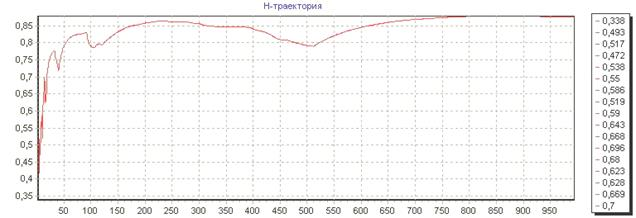
Рис.5(а): 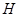–траектория временного ряда

 

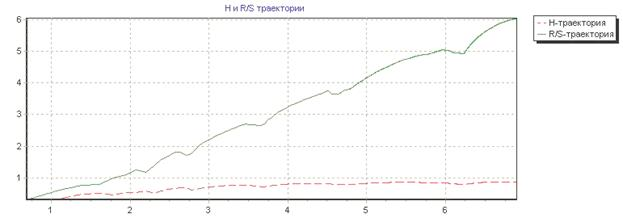
Рис.5(б): R/S-траектория временного ряда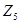

 

В результате R/S-анализа были получены следующие результаты, которые являются общими для всех рассматриваемых в работе рядов:

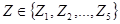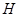·         Для любого временного ряда , его -траектория после некоторых своих первых значений оказывается в зоне «черного шума», позволяя говорить о трендоустойчивости соответствующих временных рядов и присущему им эффекту долговременной памяти.

·         Для каждого из рядов 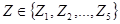 можно оценить количество первых элементов (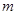), после которых показатель Херста переходит в зону «черного шума». Эта величина характеризует минимально допустимый объем выборки из временного ряда, которая несет информацию о будущих значениях данного временного ряда, т.е. позволяет строить прогноз поведения временного ряда. Соответствующие значения  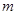для каждого из временных рядов приведены ниже в таблице 2.

 

Таблица 2: Число элементов временного ряда, после которых показатель Херста переходит в область «черного шума»

 

·         Наличие эффекта долговременной памяти может быть также доказано R/S-анализом временных рядов 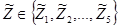, где 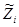 - временной ряд, полученный из ряда  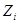случайным перемешиванием его элементов. На рисунке 6 изображена 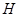-траектория временного ряда 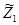, полученного случайным перемешиванием элементов временного ряда 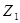. Показатель Херста для временного ряда  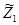оказался существенно меньше, соответствующих значений для временного ряда 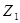, что также свидетельствует о наличие эффекта долговременной памяти у временного ряда .

 

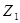Рис. 6: 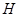-траектория временного ряда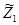

 

·         Результаты R/S-анализа позволяют также утверждать, что некоторым из рассматриваемых временных рядов присуще свойство цикличности, а точнее квазицикличности. Причем анализ R/S-траектории свидетельствует о том, что точки смены тренда чаще всего соответствуют окончанию квазициклов. Дополнительное разложение ряда на квазициклы позволит оценить глубину долговременной памяти ряда. В данной работе ярко свойство квазицикличности проявляется у рядов 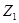, , 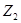 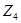и .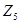

·         Для выявления свойства квазицикличности временного ряда и определения глубины долговременной памяти временного ряда проведения одного лишь R/S-анализа может быть недостаточно. Требуется привлечение дополнительных методов и алгоритмов (например, механизма фазовых траекторий и агрегирования).

·         Свойство квазицикличности наименее выражено у временного ряда 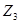. Это свидетельствует о том, что с одной стороны, предпрогнозной информации, полученной методами R/S-анализа, не достаточно для описания эволюционного процесса данного временного ряда, а с другой стороны характеризует вложения в соответствующий финансовый инструмент как «относительно безрисковые». Последний вывод хорошо согласуется с практикой торгов по облигациям федерального займа на ММВБ.

Основным результатом работы является вывод о возможности проведения предпрогнозного анализа финансовых временных рядов с помощью алгоритма нормированного размаха Херста (методом R/S-анализа). В результате этого анализа можно сделать вывод о наличии у временного ряда эффекта долговременной памяти, оценить ее глубину, выявить наличия циклов (квазициклов). Вместе с тем R/S-анализ не является исчерпывающим инструментом предпрогнозного исследования временных рядов, так как он не всегда дает полную информацию о поведении временного ряда без привлечения дополнительных методов и алгоритмов.

 

Литература

1.      Петерс Э. Хаос и порядок на рынках капитала. Новый аналитический взгляд на циклы, цены и изменчивость рынка: Пер.с англ. -М.: Мир. 2000. -333с.

2.      Федер Е Фракталы. - М.: Мир. 1991.

3.      Mandelbrot, В. The Fractal Geometry of Nature. New York: W. H. Freeman, 1983.

4.      Петерс Э. Фрактальный анализ финансовых рынков: Применение теории Хаоса в инвестициях и экономике. – М.: Интернет-трейдинг, 2004. –304с.