Для исчисления системы компромиссно-равновесных цен по модели Кардаша предложен модифицированный итерационный процесс, обладающий быстрой сходимостью и большей устойчивостью.
Концепция компромиссного анализа рыночной экономики предлагает нетрадиционный подход к моделированию и анализу экономических систем, учитывающий компромиссную стоимостную сбалансированность интересов субъектов экономики. Ключевая идея этой концепции состоит в том, что конфликтные интересы экономических агентов согласуются на основе конфликтно-компромиссного рыночного механизма [1, 2].
В рамках концепции рыночных компромиссов построена модель компромиссно-равновесного ценообразования (модель Кардаша) в виде следующей системы нелинейных уравнений [1, 2, 3, 4]
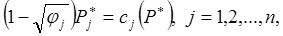 или
или
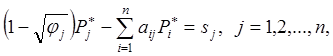 (1)
(1)
где 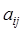 – затраты в натуральных единицах i-го продукта на единицу j-го продукта;
– затраты в натуральных единицах i-го продукта на единицу j-го продукта; 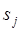 – удельные затраты труда на единицу j-го продукта;
– удельные затраты труда на единицу j-го продукта; 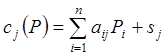 – себестоимость единицы j-ой продукции;
– себестоимость единицы j-ой продукции; 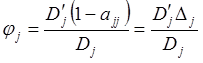 – коэффициент Кардаша, где
– коэффициент Кардаша, где 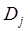 – максимально возможная сумма платежных средств на рынке j-го товара;
– максимально возможная сумма платежных средств на рынке j-го товара; 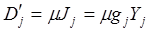 – минимально необходимая для конкурентоспособности прибыль на задействованный в j-ой товарном секторе капитал
– минимально необходимая для конкурентоспособности прибыль на задействованный в j-ой товарном секторе капитал 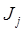 при норме рентабельности капитала
при норме рентабельности капитала 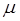 и капиталоемкости
и капиталоемкости 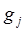 ;
; 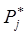 – компромиссно-равновесная цена на рынке j-го товара.
– компромиссно-равновесная цена на рынке j-го товара.
Разрешая систему (1) относительно неизвестного вектора 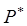 , получим
, получим
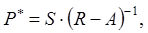 или
или 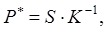 (2)
(2)
где 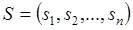 – вектор-строка с компонентами
– вектор-строка с компонентами 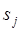 ;
; 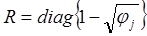 – диагональная матрица с коэффициентами по диагонали
– диагональная матрица с коэффициентами по диагонали 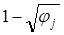 ;
; 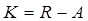 – матрица рыночных компромиссов.
– матрица рыночных компромиссов.
В [2, 3] для исчисления системы компромиссно-равновесных цен по модели (2) предлагается следующий итерационный алгоритм
1°. 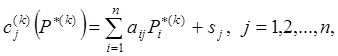 (3)
(3)
2°. 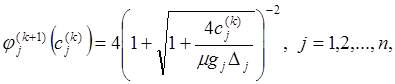 (4)
(4)
3°. 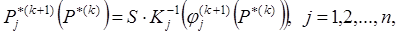 (5)
(5)
где 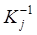 – j-ый столбец матрицы, обратной к матрице
– j-ый столбец матрицы, обратной к матрице 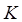 .
.
Однако, можно заметить, что в итерационном процессе (3)-(5) текущие значения цены 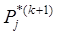 и коэффициента Кардаша
и коэффициента Кардаша 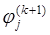 рассчитываются на основе себестоимости
рассчитываются на основе себестоимости 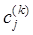 предыдущего шага. Такое построение итерационного алгоритма можно интерпретировать как переход от одного производственного цикла к другому по итерациям [2]. С учетом этой идеи, можно построить модифицированный итерационный процесс следующего вида
предыдущего шага. Такое построение итерационного алгоритма можно интерпретировать как переход от одного производственного цикла к другому по итерациям [2]. С учетом этой идеи, можно построить модифицированный итерационный процесс следующего вида
1°. 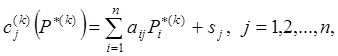 (6)
(6)
2°. 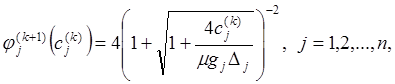 (7)
(7)
3°. 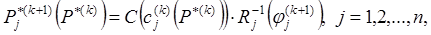 (8)
(8)
где 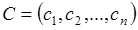 – вектор-строка из себестоимостей
– вектор-строка из себестоимостей 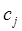 ,
, 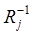 – j-ый столбец матрицы, обратной к матрице
– j-ый столбец матрицы, обратной к матрице 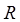 .
.
Предложенный модифицированный итерационный процесс (6)-(8) в противоположность процессу (3)-(5) обладает рядом преимуществ, а именно:
1) обращение диагональной матрицы 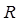 является менее затратной вычислительной операцией по сравнению с обращением недиагональной матрицы
является менее затратной вычислительной операцией по сравнению с обращением недиагональной матрицы 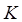 .
.
2) в процессе обращения матрицы 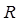 погрешность округления будет значительно меньше, чем при обращении матрицы
погрешность округления будет значительно меньше, чем при обращении матрицы 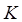 .
.
3) монотонное поведение итерационных приближений при матрице 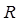 обеспечивает быструю сходимость численного метода к вектору равновесных цен
обеспечивает быструю сходимость численного метода к вектору равновесных цен 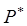 . При матрице
. При матрице 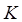 итерационные приближения имеют колебательный характер, что обуславливает медленную сходимость метода.
итерационные приближения имеют колебательный характер, что обуславливает медленную сходимость метода.
Таким образом, построенный итерационный процесс (6)-(8) является более устойчивым в смысле накопления вычислительных погрешностей и обладает лучшей сходимостью по сравнению с процессом (3)-(5). Кроме того, в ходе исследования было установлено, что итерационный алгоритм (6)-(8) обладает свойством «компромиссно-сбалансированной» сходимости. Последнее означает, что решение, получаемое итерационным расчетом по (6)-(8), всегда оказывается «компромиссно-сбалансированным», т.е. матрица 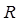 является неотрицательно обратимой
является неотрицательно обратимой 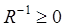 и
и 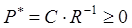 . Если же вычисления осуществляются по алгоритму (3)-(5), то уже на первой итерации приближенное решение может не попасть в область «компромиссной продуктивности».
. Если же вычисления осуществляются по алгоритму (3)-(5), то уже на первой итерации приближенное решение может не попасть в область «компромиссной продуктивности».
Литература:
1. Кардаш В.А. Компромиссный анализ рыночной экономики. – Ростов-на-Дону: Изд-во СКНЦ ВШ, 2002. – 140 с.
2. Кардаш В.А. Конфликты и компромиссы в рыночной экономике. – М.: Наука, 2006. – 248 с.
3. Кардаш В.А. Исчисление рыночных компромиссов // Обозрение прикладной и промышленной математики. ‑ 2004. - Т.11, Вып.1. – С. 41-50.
4. Кардаш В.А. Компромиссный анализ равновесных рынков // Математические методы в физике, технике и экономике / Юж.-Рос. гос. техн. ун-т (НПИ). – Новочеркасск: Ред. журн. Изв. вузов. Электромеханика, 2004. – С. 66-78.







