Методы распознавания речи



С развитием технологий человек становится окружен все большим количеством электронных устройств. Вопрос удобства взаимодействия с этими устройствами еще не до конца решен. Одно из основных направлений разработок с этой области — системы распознавания речи. Исследования возможностей перевода человеческой речи в текст ведутся еще с середины XX века, и на сегодняшний день существует несколько основных подходов.

Распознавание речи включает в себя два основных этапа: предварительную обработку сигнала и его классификацию.

Предварительная обработка

На этапе предварительной обработки исходный сигнал преобразуется в векторы признаков, на основе которых затем будет произведена классификация. Этот этап может включать в себя следующие шаги:

– преобразование сигнала из аналоговой формы в цифровую;

– применение фильтров для подавления шумов;

– выделение границ речи;

– выделение признаков сигнала.

Наиболее распространенные методы выделения признаков — это метод мел-частотных кепстральных коэффициентов и метод кепстральных коэффициентов на основе линейного предсказания.

Мел-частотные кепстральные коэффициенты (MFCC)

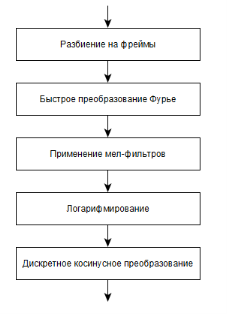
Рис. 1. Получение мел-частотных кепстральных коэффициентов

Пример алгоритма вычисления коэффициентов представлен на рисунке 1 и включает в себя следующие шаги:

1. Исходный сигнал разбивается на фреймы. Их размер обычно составляет от 10 до 40 мс. Фреймы накладываются друг на друга.
2. К каждому фрейму применяется быстрое преобразование Фурье.
3. Переход к мел-шкале.

Мел — это психофизическая единица высоты звука. Человек лучше различает звуки низкой частоты, чем высокой. На мел-шкале равное изменение частоты в мелах соответствует равному изменению ощущения высоты тона. То есть человек определит звук с частотой в 1000 мел в два раза “ниже”, чем 2000 мел, но для звуков частотой в 1000 герц и 2000 герц нет. Перевод герц в мелы происходит по формуле

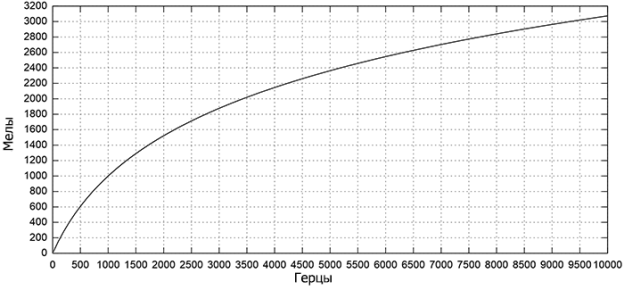
Рис. 2. Мел-шкала

Отображение сигнала на мел-шкалу происходит с помощью блока треугольных фильтров (рис. 3).

4. Набор полученных на предыдущем шаге значений логарифмируется.
5. Для получения кепстральных характеристик применяется дискретное косинусное преобразование.

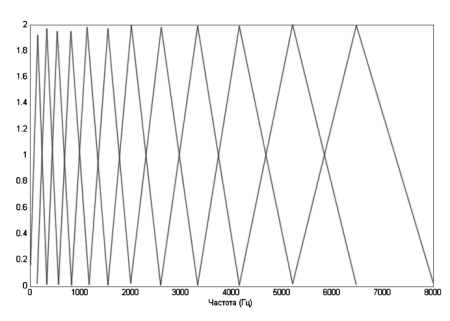
Рис. 3. Мел-фильтры

Кепстральные коэффициенты на основе линейного предсказания (LPCC)

Линейное предсказание речи основано на линейной модели речеобразования, разработанной Фантом в 50-х годах XX века.

Проблему линейного предсказания можно сформировать так: по значениям набора данных надо предсказать значение данных в последующей точке .

Пусть s (i) {\displaystyle s(i)} — анализируемый цифровой сигнал. При линейном предсказании оценка текущего отсчёта сигнала s ^ (i) {\displaystyle {\hat {s}}(i)} формируется как линейная комбинация предшествующих отсчётов:

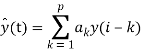
Задача линейного предсказания состоит в том, чтобы найти такой набор коэффициентов {a_k}, для которого средний квадрат ошибки (y(t) — ŷ(t))² минимален.

Коэффициенты линейного предсказания можно получить решением системы уравнений. Для получения кепстральных коэффициентов к коэффициентам линейного предсказания применяется дискретное косинусное преобразование.

Распознавание

После получения набора признаков необходимо на их основе определить, к что за звук или слово находилось в исходном сигнале. Наиболее распростаненные методы — это скрытые марковские модели и нейронные сети.

Скрытые марковские модели

Скрытая марковская модель — это модель из N скрытых состояний X и M наблюдаемых значений Y, определяется как тройка λ = (A,B,π), где А — матрица вероятностей переходов между состояниями, В — матрица вероятностей наблюдений выходных значений для каждого из состояний X, π — вектор вероятностей начальных состояний.

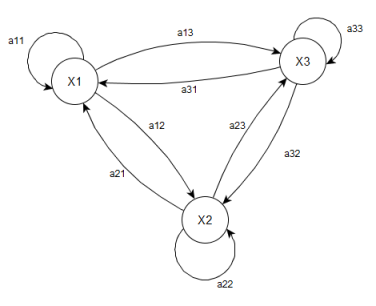
Рис. 4. Пример диграммы переходов в скрытой марковской модели

В обычной марковской модели состояние видимо наблюдателю, поэтому вероятности переходов — единственный параметр. В скрытой марковской модели можно наблюдать только переменные, на которые оказывает влияние данное состояние. Каждое состояние имеет вероятностное распределение среди всех возможных выходных значений. Поэтому последовательность символов, сгенерированная моделью, даёт информацию о последовательности состояний.

Существует три основных задачи для скрытых марковских моделей.

Задача 1. Дано: наблюдаемая последовательность O = O₁, O₂, …, O_T и модель λ = (A,B,π). Необходимо вычислить вероятность появления указанной последовательности для данной модели. Решение этой задачи непосредственно связано с задачей распознавания речи. Если, например, состояния модели соответствуют отрезкам времени, в которые снимаются параметры речевого сигнала, и в каждом из этих состояний (отрезков) параметры речевого сигнала принимают некоторые значения, которые мы представляем в виде O={o₁,o₂,…o_τ}, то решив задачу нахождения вероятности появления этой последовательности для каждой из имеющихся у нас моделей λ={A,B,π}, соответствующих, например, фонемам, мы можем выбрать ту из фонем, которая в наибольшей степени соответствует исходному отрезку речевого сигнала. А это и значит распознать речевую единицу — фонему. Для решения этой задачи применяется алгоритм прямого-обратного хода.

Задача 2. Дана последовательность наблюдений O={o1,o2,…oτ} и модель λ={A,B,π}. Необходимо выбрать последовательность состояний Q={q1,q2,…qτ}, которая с наибольшей вероятностью порождает указанную последовательность. Данные, полученные при решении этой задачи используются для изучения поведения полученной модели. Эта задача решается алгоритмом Витерби.

Задача 3. Дана последовательность наблюдений O={o₁,o₂,…o_τ} и модель λ={A,B,π}. Необходимо подобрать параметры модели так, чтобы максимизировать вероятность данной последовательности наблюдений. Это задача обучения модели на наборах входных данных. Для решения этой задачи используется алгоритм Баума-Велша.

Нейронные сети

Нейронная сеть — это математическая модель, построенная на принципах работы человеческого мозга.

Нервная система и мозг человека состоят из нейронов, соединенных друг с другом нервными волокнами, которые способны передавать электрические импульсы. Нейрон состоит из тела, и отростков нервных волокон двух типов — дендритов, по которым принимаются импульсы, и одного аксона, по которому нейрон передает импульсы.

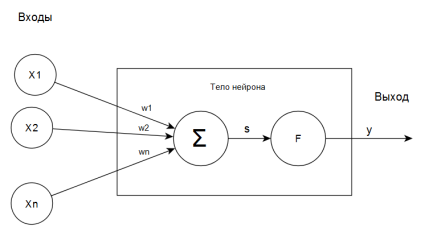
Рис. 5. Схема искусственного нейрона

На основе нейрона был создан искусственный нейрон (рис. 5). Его синапсы представлены весовыми коэффициентами w₁, …, w_n. Текущее состояние нейрона вычисляется по формуле

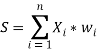
Результат суммирования передается в активационную функцию F. Существуют различные виды активационных функций: пороговая, линейная, экспоненциальная и другие. Но наибольшее распространение получила логистическая функция, которая вычисляется по формуле

где α — коэффициент наклона. Изменяя его можно строить функции с различной крутизной.

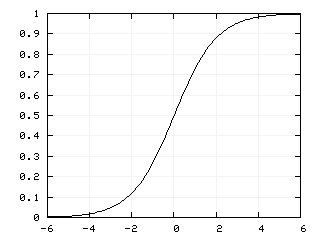
Рис. 6. График логистической функции

Особенность этой функции состоит в том, что она способна усиливать слабые сигналы и не приводить к насыщению от сильных сигналов.

Нейронная сеть может состоять из одного или нескольких слоев. Многослойные сети способны решать некоторые задачи, недоступные однослойным сетям, и обладают большими вычислительными возможностями. Количество входов сети — это количество обрабатываемых признаков. Количество выходов — это количество возможных вариантов “ответов” распознавания.

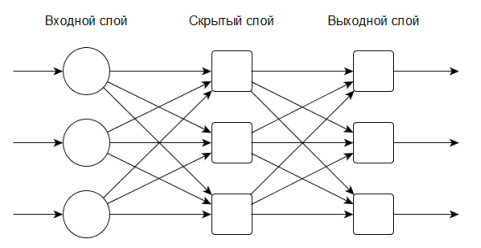
Рис. 7. Пример многослойной нейронной сети

Для того, чтобы, подав на вход нейронной сети вектор признаков сигнала, получить от нее близкий к действительности ответ, ее нужно предварительно обучить. Обучение осуществляется путем последовательной подачи векторов признаков и одновременно с этим изменением весовых коэффициентов. Порядок изменения определяется выбранным алгоритмом обучения. Обучение бывает двух видов: с учителем и без учителя.

Обучение с учителем преполагает, что для каждого входого вектора нам известен заранее выходной вектор, то есть обучающая выборка состоит из пар входных и выходных векторов. Ошибка распознавания, которая вычиляется как разность выхода сети и известного выходного вектора. Обучение состоит в минимизации этой ошибки и завершается, когда она достигнет приемлемого значения.

Обучение без учителя предполагает, что ответов для входных векторов не имеется. Обучающий алгоритм должен изменить веса так, чтобы схожие входные векторы, поданные сети, давали сходные ответы.

Литература:

1. L. Rabiner, Biing-Hwang Juang. Fundamentals of Speech Recognition.1993. — 507 с.
2. Маркел Дж.Д., Грэй А. X. Линейное предсказание речи: Пер. с английского / Под редакцией Ю. Н. Прохорова и В. С. Звездина. — М.: Связь, 1980
3. Taabish Gulzar, Anand Singh. Comparative Analysis of LPCC, MFCC and BFCC // International Journal of Computer Applications. — 2014. — № 101(12). — С. 22–27.
4. Смит С. Цифровая обработка сигналов. Практическое руководство для инженеров и научных работников. — М.: Додэка-XXI, 2012. — 720 с.
5. Круглов В. В., Борисов В. В. Искусственные нейронные сети. Теория и практика. — 2-е изд. — М.: Горячая линия-Телеком, 2002. — 382 с.