Компьютерное моделирование процессов распыла и дисперсии капель жидких топлив в камере сгорания



В настоящее время, несмотря на прилагаемые усилия по освоению и использованию возобновляемых источников энергии, 85 % всей энергии, потребляемой в мире, получают от сжигания ископаемых видов топлива. Как показывает статистика, 39 % общего энергопотребления приходится на сжигание жидких топлив и 97 % от этого общего производства энергии используется в транспортном секторе. В то время как мы продолжаем пользоваться жидкими топливами, как основным источником энергии, первостепенное значение имеет повышение эффективности и минимизация воздействия на окружающую среду устройств, деятельность которых направлена на сжигание этого вида топлив. Во многих странах мира в последнее время резко возросли требования к качеству топлив с точки зрения их экологической безопасности.

Разработка улучшенных систем преобразования энергии, имеющих более высокую эффективность и низкий уровень выбросов, занимает основное место в сокращении производства парниковых газов. Особенно это касается диоксида углерода (СО₂) и этот факт является гарантией того, что в будущем воздушный транспорт не приведет к нежелательному ухудшению озонового слоя стратосферы [1–2].

Необходимость детального исследования физико-химических процессов, протекающих при горении жидких топлив, определена возросшими требованиями к эффективности работы различных технических устройств, точности прогнозирования воспламенения и обусловлена современными экологическими требованиями по охране окружающей среды. Эффективность работы различных технических устройств, в частности, двигателей внутреннего сгорания в значительной степени базируются на результатах фундаментального исследования физико-химических процессов горения.

Горение жидких топлив отличается рядом специфических особенностей, обусловленных протеканием химических реакций в условиях динамического и теплового взаимодействия реагентов, интенсивного массопереноса при фазовых превращениях, а также зависимостью параметров процесса, как от термодинамического состояния системы, так и от ее структурных характеристик. Так как исследование горения невозможно без его детального изучения, то на первый план выходит проблема фундаментального исследования закономерностей процессов тепломассопереноса при сжигании различных видов топлив.

В связи со сказанным выше особое значение и актуальность приобретает интенсификация производства, снижение материалоемкости оборудования, экономное расходование топлива, охрана окружающей среды. Весьма важной является задача создания научных основ интенсивных технологических процессов, обеспечивающих комплексное использование топлива и его отходов, исключающих вредное воздействие производства на биосферу. Новая стратегия охраны природы и энергосбережения предполагает выбор наиболее эффективных достижений научно-технического прогресса. Среди них особо выделяются три основные группы мероприятий: утилизационные, энергетической модернизации, интенсивного энергосбережения.

Большинство течений по природе своей имеют турбулентный характер и состояние турбулентности при движении потока сильно влияет на такие параметры течения, как перенос импульса, температуры и концентрации веществ в смеси.

Данная статья посвящена важному исследованию с точки зрения современной физики горения проблемы численного моделирования распыла и горения жидкого топлива при высокой турбулентности.

Решение задачи о распылении и горении жидкого топлива осуществляется методами численного моделирования с использованием дифференциальных уравнений, описывающих турбулентное течение при наличии химических реакций, и представлены основными уравнениями: неразрывности, движения, внутренней энергии, k-ε модель турбулентности, а так же начальными и граничными условиями [3–6].

Уравнение неразрывности для компоненты реакции m имеет вид:

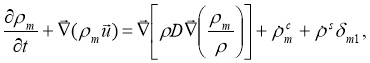(1)

где D — коэффициент диффузии, _m — массовая плотность жидкой фазы,  — полная массовая плотность, – химический источниковый член; — источниковый член вследствие впрыска; u– скорость жидкости.

Уравнение неразрывности для жидкости, имеет следующий вид:

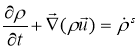.(2)

Уравнение движения для смеси жидкостей:

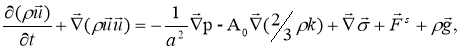(3)

где р — давление жидкости,  — безразмерная величина, A₀ равно 0 при ламинарном течении и 1 — при турбулентности. Тензор вязких напряжений имеет вид:

(4)

Здесь µ — динамическая вязкость жидкости, — коэффициент вязкости, g — ускорение свободного падения и I — удельная внутренняя энергия.

Уравнение внутренней энергии представлено ниже:

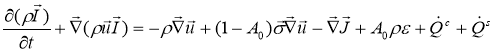,(5)

где– источниковый член, обусловленный тепловыделением в результате химической реакции и – тепло, которое приносит впрыскиваемое топливо. Вектор теплового потокаJскладывается из электропроводности и переноса энтальпии.

При использовании модели турбулентности (А₀=1) решаются уравнения для кинетической энергии турбулентности k и скорости ее диссипации ε :

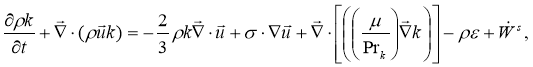(6)

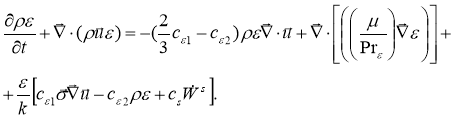(7)

Величина возникает вследствие взаимодействия с распылителем. Константы определяются из эксперимента [6].

В работе была использована модель камеры сгорания в форме цилиндра, высота которой 15 см, диаметр 4 см. Общий вид камеры сгорания представлен на рисунке 1. Расчетная область состоит из 650 ячеек. С помощью сопла, которое располагается в центре нижней части камеры сгорания, впрыскивается жидкое топливо. Площадь форсунки равна 210–⁴ см². Температура стенок камеры сгорания 353 К. Начальная температура газа в камере сгорания 900 К, топливо впрыскивается при 300 К. Начальный радиус впрыскиваемых капель 25 мкм. Угол, при котором впрыскиваются капли, равен 10⁰. Давление в камере сгорания составляет 80 бар, скорость впрыска жидкого топлива равна 250 м/с.

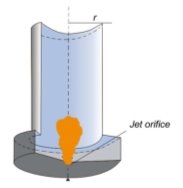
Рис. 1. Общий вид камеры сгорания

В данной работе были использованы два вида жидких топлив: октан (С₈Н₈) и додекан (С₁₂Н₂₆). Химические реакции горения этих топлив в камере сгорания представлены ниже:

,

.

Эти реакции приводят к образованию углекислого газа и воды.

На следующих рисунках показаны результаты численного моделирования горения октана и додекана в камере сгорания. На рисунке 2 представлено распределение капель октана и додекана по размерам по высоте камеры в момент времени t=2,5 мс. В момент времени t=2,5 мс капли октана и додекана поднялись на высоту камеры равной 0,62 см и 0,72 см. Анализируя поведение додекана, можно отметить, что размеры его капель чуть больше капель октана. Обращая внимание на распределение октана и додекана по радиусам можно заметить, что капли додекана быстрее испаряются и плотность распределения более высокая. Также со временем размер капель октана растет.

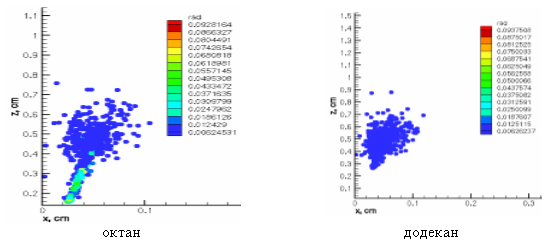
Рис. 2. Распределение капель октана и додекана по радиусам по высоте камеры сгорания в момент времени t=2,5 мс

На рисунке 3 показаны поля температуры в камере сгорания при горении октана и додекана в момент времени 2,5 мс. Эти графики свидетельствует о том, что при горении октана большая часть камеры прогревается до 987,192 К, а при горении додекана в камере дольше всего держится значение температуры равное 1003,05 К. В момент времени t=2,5 мс в ядре температурного факела при горении октана температура достигает значения 2687,32 К. При горении додекана максимальная температура составила 2679,87 К, а температура всей камеры, кроме зоны факела, достигает 1003,05 К. Для двух рассматриваемых видов топлив (октан и додекан) при распределении температур наблюдается следующая картина: область, охватываемая максимальной температурой, при горении обоих топлив в различные моменты времени почти одинаковая, но по сравнению с октаном весь объем камеры при сжигании додекана быстрее прогревается до высоких значений температуры. Анализируя полученные данные, можно сделать вывод, что процесс горения октана и додекана происходит в газовой фазе, и по всему объему камеры сгорания наблюдается равномерное распределение температуры.

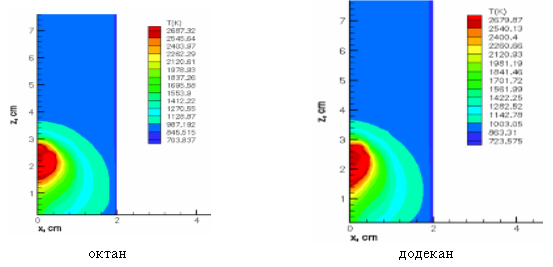
Рис. 3. Профиль температуры в камере сгорания при горении октана и додекана в момент времени t=2,5 мс

На следующем рисунке 4 представлены поля концентрации обоих видов топлив в момент времени 2,5 мс. При сравнении октана и додекана можно увидеть, что пары обоих видов топлив поднимаются на различные высоты. К примеру, в момент времени t=2,5 мс пары октана поднимаются на высоту камеры 2,3 мс, а пары додекана в это же время находятся на высоте 2,6 см.

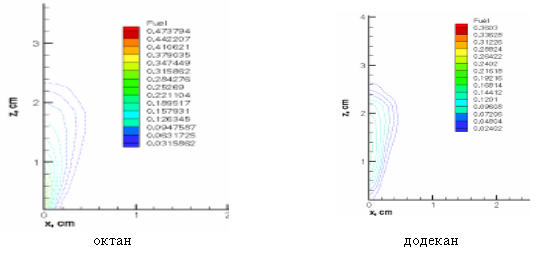
Рис. 4. Распределение паров октана и додекана по высоте камеры сгорания в момент времени 2,5 мс

Таким образом, по полученным результатам по горению двух видов жидких топлив можно сделать заключение:

– капли октана и додекана поднимаются на различные высоты, но имеют почти одинаковые размеры;

– при горении обоих видов топлив температура в камере сгорания достигает максимальных значений, но при горении октана в большей части камеры сгорания сохраняется меньшая температура, чем при горении додекана;

– концентрации паров топлив (октан и додекан) в начальные моменты времени имеют почти одинаковые значения, но с течением времени достигают максимальных значений по всему объему камеры.

Литература:

1. Askarova A., Bolegenova S., Bekmukhamet A., Ospanova Sh., Gabitova Z. Using 3D modeling technology for investigation of conventional combustion mode of BKZ-420–140–7C combustion chamber // Journal of Engineering and Applied Sciences. — 2014. — Vol.1, № 9. — P. 24–28.
2. Askarova, A. S., Karpenko, E. I., Messerle, V. E., Ustimenko, A. B. Mathematical modelling of the processes of solid fuel ignition and combustion at combustors of the power boilers // 7th International Fall Seminar on Propellants, Explosives and Pyrotechnics. — Xian, 2007. — Vol. 7. — P. 672–683.
3. Askarova, A.S., Ustimenko, A. B., Bolegenova, S. A., Maksimov, V. Yu. Numerical simulation of the coal combustion process initiated by a plasma source // Thermophysics and aeromechanics. — 2014. — Vol 21, issue 6. — P. 747–754.
4. Bolegenova, S.A., Maximov, V.Y., Bekmukhamet, A, Beketayeva, M.T.Gabitova, ZK., et al. Computational method for investigation of solid fuel combustion in combustion chambers of a heat power plant // High temperature. — 2015. — Vol. 5, issue 5. — P. 751–757.
5. Amsden A. A., O'Rourke P. J., Butler, T. D. KIVA-II: A computer program for chemically reactive flows with sprays. — Los Alamos, 1989. — 160 с.
6. Amsden D. C., Amsden A. A., The KIVA Story: A Paradigm of Technology Transfer // IEEE Transactions on Professional Communication Journal. -1993. — Vol.36, № 4. — P. 190–195.