Ключевые слова: фазированная антенная решетка, возбуждение, оптимизация, коэффициент усиления, направленность
Фазированные антенные решетки (ФАР) уже давно используются в микроволновых частотах, преимущественно в радиолокации. Что касается коротковолновых, таких систем не так широко известны. Тем не менее, возможность ФАР, используя в диапазоне коротких волн в последнее время вызывают значительный интерес исследователей. Во многом это объясняется тем, что современные цифровые методы обработки сигнала, которые в наибольшей степени подходят для этой группы, обеспечивают широкие возможности управления для таких систем.
В последнее время в теории оптимизации возбуждения таких антенных решеток рассматривается [1]. В этой работе, критерий оптимизации был выбран как максимум излучения в заданном направлении (оптимизация коэффициента усиления антенной системы) в условиях ограниченной мощность входа антенной системы. Хотя в случае передающих антенн такого критерия оптимизации вполне закономерен, иногда это может быть необходимо для выполнения оптимизации для максимальной направленности антенной системы. Конечно, если нет серьезных потерь, так как, как правило, в СВЧ диапазоне, коэффициент усиления совпадает с коэффициентом направленного действия. В этом случае модификация теории не требуется. Тем не менее, в коротковолновом диапазоне элементы антенны часто используются с существенными потерями. При таких условиях коэффициент усиления не совпадает с коэффициентом направленного действия. Это недавно было отмечено в [2].
Как описывалось в [1], поля излучения антенных систем, имеющих точки питания, могут быть представлены в виде линейной комбинации частных составляющих. Это тривиальное следствие линейности антенной системы по отношению к возбуждению. Естественно, далее параметры антенной системы считаются заданными, учитываются только оптимизация ее возбуждения.
Частный компонент представляет собой электромагнитное поле, которое образуется тогда, когда только одна точка питания возбуждается. Обязательно, количество частных компонентов равно числу точек питания. Величин, характеризующая возбуждение такой точки может быть, как ток и напряжение в этой точке. В [1] ток был выбран в качестве возбуждающего действия, здесь мы выбираем напряжение. Для того, чтобы вычислить частотные составляющие, необходимо найти поле излучения, в котором совпадает точка подачи питания на блок напряжения, все остальные точки находятся в коротком замыкании. Такой расчет можно сделать, используя любые компьютерные коды, предназначенные для анализа антенн, в частности при помощи NEC-2 [3].
Обозначим комплексные амплитуды напряжения в точке питания как 
, индекс 
обозначает определенные точки питания. Поле излучения (не имеет значения, магнитное или электрическое, можно использовать любое) для случая, когда одна точка питания с числом возбуждений, обозначается 
, другие точек питания подразумевается закороченными. Далее верхним индексом 
выделяются различные компоненты векторного поля. Из-за линейности антенной системы, в случае когда все не равны нулю, то результирующее поле 
может быть записано следующим образом:
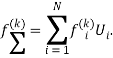(1)
Мощность излучения потока Theradiation
:
(2)
где верхнее подчеркивание означает комплексное сопряжение, а в свободном пространстве волновое сопротивление при 
— это магнитное поле или обратное значение при — это электрическое поле. Далее фактор 
не имеет значения и не учитывается.
Используя вышеприведенные уравнения, интенсивность мощности излучения может быть записана в виде следующей билинейной формы возбуждающего напряжения:
(3)
Где
(4)
Очевидно, что уравнение (3) можно переписать в матричной форме:
(5)
где 
-квадратная матрица, имеющая 
компоненты, 
является одним столбцом матрицы, имеющей компонентов, верхний индекс “+” означает эрмитово-сопряжённую матрицу. Матрица может быть также представлена в матричной форме следующим образом:
(6)
где является одной матрицей содержащей столбцы 
.
Следует подчеркнуть, что
это функция от вектора, который определяет точку, при которой электромагнитное поле вычисляется. Следовательно, также является функцией этого аргумента. Как правило, мы имеем в виду такие аргументы без конкретного их указания.
Соответственно, мощность суммарного излучение 
может быть записан следующим образом:
(7)
Где 
такой поверхности, охватывающей антенну, есть сила направленности потока по нормали к этой поверхности в других точках. По сути, поверхность должна быть по центру полусферы при расположении антенной системы, имеющей радиус значительно больше длины волны излучения и размера антенной системы. В этом случае, в зависимости от точки поверхности сводится к функции двух углов: полярный 
и азимутальный 
. Таким образом, (7) можно представить следующим образом:
(8)
Так как не зависит от углов, (8) можно переписать как
(9)
где матрица 
определяется следующим образом:
(10)
Направленность 
это ничто иное, как соотношение излучаемой интенсивностью мощности в заданном направлении к излучаемой интенсивностью мощности усредненной по всем направлениям. Очевидно, что первое это 
(согласно (5)), а второе 
(согласно (9)). Следовательно,
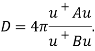(11)
Таким образом, проблема коэффициента направленности действия максимума главного лепестка можно записать следующим образом:
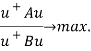(12)
Очевидно, что эта задача эквивалентна следующей задаче оптимизации условной максимизации
(13)
Действительно, в левой части (12) инвариантна по отношению к любому изменению вектора нормализации. Оптимизация может быть сделана только с точностью до нормировки. Так что, можно выбрать любую нормализацию, в частности 
.
Если нет потерь, то коэффициент усиления антенны 
и равен . Так что, в случае отсутствия потерь оптимизационной задачи (13) эквивалентно случаю, рассмотренному в [1], хотя сейчас матрица задается по-разному. Так что, в случае отсутствия потерь оптимизационная задача (13) эквивалентна случаю, рассмотренному в [1], хотя сейчас матрица задается по-разному. Этот факт является формальным математическим доводом эффекта описанным в [2].
Как видно из (13), что математически проблема коэффициента направленности действия максимума главного лепестка идентичена случаю, рассмотренному в [1; 2]. Разница только в том, как матрица определяется. В [1; 2] эта матрица была определена с помощью матрицы 
из входной проводимости антенной системы (общий численный фактор можно опустить):
(14)
В противном случае, если направленность должна быть максимальной, тогда матрица определяется уравнением (10). Таким образом, в отличие от [1; 2], в то время как направленность максимальна, необходимо просчитать только радиационное поле. Это можно сделать с помощью моделирования антенны программное обеспечение, такое как, например, NEC-2. Затем, надо использовать уравнения (4), (10) и, после численного интегрирования, найти матрицу . Дальнейшая оптимизация не отличается от той, что рассмотрена в [1; 2]. Естественно, чтобы обеспечить численное интегрирование в (10) поле излучения должно быть рассчитано не на один набор углов и , но и для двумерной сетки из этих углов.
Оптимизационная задача (13) может быть упрощена. Для этого мы вводим новую переменную матрицы 
выглядящую следующим образом:
(15)
Поскольку матрица
является Эрмитовой и положительна определена, расчет 
не является фундаментальной проблемой. Более того, из изложенного далее будет ясно, что /явная форма не нужна.
Подставляя (15) в (13) получаем следующую задачу оптимизации:
(16)
Где
(17)
Эта оптимизационная задача может быть легко решена. Можно доказать, что оптимальные -нормированный собственный вектор Эрмитовой матрицы с соответствует максимуму собственных значений. Более того, даже не нужно решать задачу о собственных значениях для матрицы 
. Причина в том, что матрица имеет максимальный ранг два (часто это ранг равен одному). Последнее является следствием того, что поле излучения имеет не более чем два независимых компонента вектора (часто один из компонентов, такой как горизонтальная составляющая, если излучатели имеют вертикальную поляризацию, можно пренебречь; в этом случае ранг матрицы-один). Можно показать, что если ранг 
, то не нормированный вектор (нормализация простая и не учитывается), соответствующее решению задачи оптимизации задается следующим уравнением
(18)
где один из столбцов матрицы (вектор) 
состоит из 
. Если 
, то решение
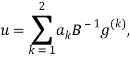(19)
где 
компоненты двумерного вектора составляющие собстенный вектор совпадающим с максимальным собственным значением 2×2 матрицы , имеющей компоненты
(20)
Данная статья наглядна показывает, что коротковолновые антенные решетки не так уж и сложны в теории. Сейчас существует множество программ, которые помогут рассчитать все параметры и промоделировать сигналы.
Литература:
- Yurkov A. S. Optimizatsiya vozbuzhdeniya peredayushih fazirovannyh antennyh re-shotok dekametrovogo diapazona dlin voln (in Russian). Omsk, 2014.
- Yurkov A. S. O vliyanii poter v zemle na rabotu chetyrehelementnoi FAR KV diapazona (in Russian) // Tehnika radiosvyazi. 2014. Issue 1 (21). P. 78–84.
