В современных биометрических системах контроля и управления доступом (БСКД) результатом обработки биометрических признаков человека является предоставление пользователю доступа к запрашиваемой информации или предоставление доступа к защищаемому объекту.
Одним из методов защиты «в глубину» таких систем является применение мультифакторной системы аутентификации. Такие системы подразумевают необходимость предоставления пользователем двух (или более) биометрических признаков для получения доступа — например, сканирование сетчатки глаза и голосовую идентификацию. Практика показывает [1], что уже при использовании двух биометрических параметров вероятность ошибок снижается до 1,5 %.
Метод, безусловно, имеет огромное преимущества, однако возникает серьезная проблема — как системе опираясь на данные нескольких устройств принять решение о предоставлении доступа.
В настоящей работе предлагается методика оценки степени доверия к заключению для случая мультифакторной биометрической аутентификации на основе алгоритма вероятностных экспертных систем, а именно — коэффициентов доверия.
Для системы мультифакторной биометрической аутентификации, состоящей из 4 модулей-сканеров: отпечатка пальца (X1), геометрии руки (X2), лица (X3), сетчатки глаза (X4), составим базу правил, исходя из статистических оценок точности данных методов [1] и ряда допущений, соответствующих знаниям экспертов. Так, точность распознавания рассматриваемых методов, определяющая степень доверия к ним, имеет следующие значения:
1. аутентификация по сетчатке глаза — 94 %;
2. аутентификация по лицу — 60–65 %;
3. аутентификация по отпечатку пальца — 89 %;
4. аутентификация по геометрии кисти руки — 91 %.
Для определения лучшей конфигурации работы модулей внутри системы БСКД рассмотрим 4 варианта правил их взаимодействия. Для разработки этих правил воспользуемсяправилами логических комбинаций из теории экспертных систем. Рассмотрим эти процедуры [2] более подробно:
1. Простейшей логической комбинацией является конъюнкция (правило типа «И») между двумя элементарными посылками:
ЕСЛИ (А И В), ТО С:![]() .
.
Согласно здравому смыслу, коэффициент определенности такой посылки равен коэффициенту определенности наименее надежной из посылок, т. е. наименьшему коэффициенту из имеющихся:
ct(A & B)=min [ct(A),ct(B)]. (1)
Такая оценка является несколько заниженной, но в большинстве практических случаев остается удовлетворительной.
2. Другой простой формой является правило, в котором используется дизъюнкция (правило типа «ИЛИ»):
ЕСЛИ (А И В), ТО С:![]() .
.
Коэффициент определенности посылки в правилах типа «ИЛИ» принимается самой надежной части, т. е. равным наибольшему коэффициенту из имеющихся:
ct(A B)=max [ct(A),ct(B)].(2)
3. В случае, когда в пользу данного заключения свидетельствуют два независимых правила:
ЕСЛИ A, ТО С; ЕСЛИ B, ТО С: ![]() ;
;![]() ,
,
то коэффициент определенности вычисляется по формуле:
ct3(C)=ct1(C)+ct2(C) — ct1(C)·ct2(C), (3)
где,ct1(C), ct2(C) — коэффициенты определенности, вычисленные в процессе срабатывания соответствующих правил.
Между тем в простых правилах вида
ЕСЛИ посылка, ТО заключение
коэффициент доверия заключения вычисляется как:
cf(заключение) = cf(посылка)∙cf(правило) (4)
Опираясь на правила, описанные выше, сформулируем 4 блока правил, отражающих взаимодействие биометрических модулей внутри одной системы. Эти варианты комбинаций представлены в таблице 1.
На основании приведенной выше точности распознавания, предположим, что при прохождении зарегистрированным пользователем процедуры аутентификации на каждом из модулей биометрической системы получаются следующие значения, соответствующие проценту схожести с эталоном, хранящимся в базе эталонов:
1. при аутентификации по сетчатке глаза (X1) — 89 %;
2. при аутентификации по лицу (X2) — 50 %;
3. при аутентификации по отпечатку пальца (X3) — 80 %;
4. при аутентификации по геометрии руки (X4) — 85 %.
Таблица 1
Варианты взаимодействия биометрических модулей внутри системы
|
Дерево вывода, соответствующее правилам |
Правила взаимодействия модулей |
|
1. Комбинация модулей с поддержкой одного заключения двумя посылками |
|
|
|
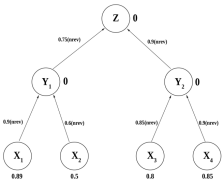
R1: ЕСЛИ X1, ТО Y1cf(R1)=0.9 R2: ЕСЛИ X2, ТО Y1cf(R2)=0.6 R3: ЕСЛИ X3, ТО Y2cf(R3)=0.85 R4: ЕСЛИ X4, ТО Y2cf(R4)=0.9 R5: ЕСЛИ Y1, ТО Z cf(R5)=0.75 R6: ЕСЛИ Y2, ТО Z cf(R6)=0.9 |
|
2. Комбинация модулей с правилами типа И |
|
|
|
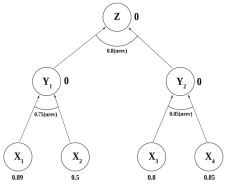
R1: ЕСЛИ X1 и X2, ТО Y1cf(R1)=0.75 R2: ЕСЛИ X3 и X4, ТО Y2cf(R2)=0.85 R3: ЕСЛИ Y1 и Y2, ТО Z cf(R3)=0.8 |
|
3. Комбинация модулей с правилами типа ИЛИ |
|
|
|
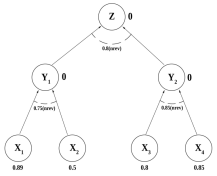
R1: ЕСЛИ X1 или X2, ТО Y1cf(R1)=0.75 R2: ЕСЛИ X3 или X4, ТО Y2cf(R2)=0.85 R3: ЕСЛИ Y1 или Y2, ТО Z cf(R3)=0.8 |
|
4. Комбинация модулей правилами типа ИЛИ и правилом типа И |
|
|
|
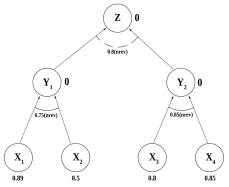
R1: ЕСЛИ X1 и X2, ТО Y1cf(R1)=0.75 R2: ЕСЛИ X3 и X4, ТО Y2cf(R2)=0.85 R3: ЕСЛИ Y1 или Y2, ТО Z cf(R3)=0.8 |
В результате расчетов с применением формул (1), (2) и (4) определим коэффициент доверия к заключению Z для каждого варианта комбинации.
Вариант 1. Комбинация модулей с поддержкой одного заключения двумя посылками.
cf(Y1) = 0,89 ∙ 0,9 = 0,801;
cf(Y1) = 0,5 ∙ 0,6 = 0,3;
cf(Y1) = 0,801 + 0,3–0,81∙0,3 = 0,8067;
cf(Y2) = 0,80 ∙ 0,85 = 0,68;
cf(Y2) = 0,85 ∙ 0,9 = 0,765;
cf(Y2) = 0,68 + 0,765–0,68∙0,765 = 0,9248;
cf(Z) = 0,8607 ∙ 0,75 = 0,645525;
cf(Z) = 0,9248 ∙ 0,90 = 0,83232;
cf(Z) = 0,645525 + 0,83232–0,645525∙0,83232 = 0,94;
Согласно этому варианту пользователь на 94 % соответствует эталону.
Вариант 2. Комбинация модулей с правилами типа И
cf(Y1) = min [0.89; 0.5] = 0.5;
cf(Y1) = 0,5 ∙ 0.75 = 0.375;
cf(Y1) = min [0.8; 0.85] = 0.8;
cf(Y2) = 0,8 ∙ 0,85 = 0,68;
cf(Z) = min [0.375; 0.68] = 0.375;
cf(Z) = 0.375 ∙ 0.8 = 0.3;
Согласно этому варианту пользователь на 30 % соответствует эталону.
Вариант 3. Комбинация модулей с правилами типа ИЛИ
cf(Y1) = max [0.89; 0.5] = 0.89;
cf(Y1) = 0,89 ∙ 0.75 = 0.6675;
cf(Y1) = max [0.8; 0.85] = 0.85;
cf(Y2) = 0,85 ∙ 0,85 = 0,7225;
cf(Z) = max [0.6675; 0.7225] = 0.7225;
cf(Z) = 0.7225 ∙ 0.8 = 0.578;
Согласно этому варианту пользователь на 57 % соответствует эталону.
Вариант 4. Комбинация модулей правилами типа ИЛИ и правилом типа И
cf(Y1) = min [0.89; 0.5] = 0.5;
cf(Y1) = 0,5 ∙ 0.75 = 0.375;
cf(Y1) = min [0.8; 0.85] = 0.8;
cf(Y2) = 0,8 ∙ 0,85 = 0,68;
cf(Z) = max [0.375; 0.68] = 0.68;
cf(Z) = 0.68 ∙ 0.8 = 0.544;
Согласно этому варианту пользователь на 54 % соответствует эталону.
Учитывая произведенные на первоначальном этапе допущения, а именно определение коэффициентов доверия для X1, X2,X3, X4, и коэффициентов доверия, присвоенных каждому правилу следует вывод, что применение независимых устройств биометрической защиты, учитывающих отдельные биометрические признаки пользователя, показывает наиболее высокую степень доверия к нему.
Литература:
- Tipton H. F., M. Krause. Information Security Management Handbook. — 5th Edition. — Boca Raton: CRC Press, 2006. — 2036 с.
- Маршаков Д. В., Фатхи В. А. Экспертные системы информационной безопасности: учебное пособие.— Ростов-на-Дону: Издательский центр ДГТУ, 2015. — 206 с.