Особое внимание уделяется обеспечению качества электроэнергии, которая должна соблюдать определённые требования. Несоблюдение требований ведёт к повреждению электрического оборудования, к росту потерь электроэнергии.
Ввиду постоянного роста количества электрических приёмников возникают высшие гармоники. А составляющие гармоник тока и напряжения ведут к возникновению проблем качества электрической энергии. На потребителей это сказывается в виде повышения стоимости электрической энергии. Под качеством электрической энергии принято понимать взаимосоответствие характеристик электроэнергии и показателей качества электроэнергии. Основными параметрами качества согласно ГОСТ 13109–2003 [1] являются колебания напряжения, отклонение частоты, несинусоидальность и несимметрия напряжения. Поэтому правильное определение параметров режима, таких как активная и реактивная мощность, а также действующие значения токов и напряжений имеет важное значение при исследовании показателей качества электроэнергии.
Определение активной, реактивной и полной мощности.
Одним из важных параметров в электроэнергетических системах является активная мощность, которой уделяется большое внимание. Активной мощностью P называется мощность, потребляемая электроприёмниками и преобразующаяся в другие виды энергии. Она имеет конкретное определение. Поэтому способы определения активной мощности никем не опровергались.
Иначе можно говорить о неактивной мощности или реактивной мощности, так как стойкого определения нет. Под ней понимают всю мощность, исключая активную. Это связано с тем, что описать процессы при несинусоидальных режимах реактивной мощностью нельзя. Реактивной мощностью называют мощность, преобразующуюся в энергию магнитных и электрических полей.
Электрические поля будут создаваться в электрооборудовании, которое характеризуется ёмкостным сопротивлением. Реактивная мощность в конденсаторах, кабелях представлена выражением
![]() .
.
А магнитные поля характеризуются индуктивным сопротивлением. В таких видах электрооборудования как, трансформаторы, двигатели реактивная мощность определяется выражением
![]() .
.
Полная мощность определяется общепризнанной формулой в случае синусоидальной нагрузки:
![]() .
.
Под полной мощностью понимают мощность, необходимую для обеспечения работы нагрузки, в случае неиспользования всей мощности при совершении полезной работы. Именно она определяет выбор электрооборудования подстанций.
Способов определения реактивной мощности существует много. Именно вопросы определения реактивной мощности являются предметом споров и обсуждений учёных. Внимание к этим вопросам связано с увеличением несинусоидальных нагрузок. Соответственно, если гармоники были невелики, то погрешность расчётов реактивной мощности была не большой. Рост высших гармоник связан с внедрением различных устройств. Источниками высших гармоник являются такие устройства, как сварочные аппараты, статические преобразователи, электродуговые печи.
Так же фактором влияния является прогресс компьютерной техники. Что значительно сокращает время и упрощает расчёты. Ранее компьютерная и измерительная техника не позволяла производить сложные расчёты реактивной мощности.
Ранее в ГОСТах никак не застрагивались несинусоидальные режимы. Поэтому проблемы определения реактивной мощности при несинусоидальных режимах являются актуальными.
Международная электротехническая комиссия (МЭК) в 1977г. предложила производить расчёт реактивной мощности по формуле
![]() .
.
Методы определения реактивной мощности при синусоидальных режимах.
Методы определения реактивной мощности при синусоидальных режимах можно разделить на две группы: методы, использующие мгновенные значения токов и напряжений и методы, использующие действующие значения токов и напряжений.
Первая группа методов, основанная на использовании мгновенных значений токов и напряжений, использует формулу, встречающуюся практически в каждом учебнике по ТОЭ.
К. С. Демирчян в [2] приводит формулу, которая справедлива лишь для синусоидального режима:
![]() .
.
Также часто встречается способ определения реактивной мощности по формуле
![]() .
.
Формула имеет место и для расчёта несинусоидальных режимов.
Также существует ещё один способ определения мощности для синусоидального режима, используя вольтамперную характеристику. Маевский в [3] предпринял попытку использования интегрального выражения. Интеграл берётся от произведения тока на функцию перпендикулярную напряжению или напротив произведения напряжения на функцию перпендикулярную тока. Мощность Маевского представлена формулой
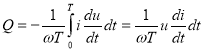 .
.
Методы определения реактивной мощности при несинусоидальных режимах.
В связи с отсутствием точной формулировки реактивной мощности при несинусоидальных режимах у учёных наблюдаются большие разногласия.
Наиболее известная формула расчёта реактивной мощности ввёл Штайнмец которую используют как для расчёта режимов с синусоидальной нагрузкой, так и с несинусоидальной:
![]() .
.
Далее Иловичем были предложены формула
![]() .
.
Буденау ввёл понятие «мощность искажение». Заметим, что учёные по-разному обозначают мощность искажения. В литературе [4, 5, 6] обозначают, как «D», также встречается такое обозначение, как «T» в [7].
Буденау считал целесообразным выделение двух составляющих Q и D, это являлось причиной превышения полной мощности над активной мощностью в несинусоидальном режиме. На рисунке 1 представлено геометрическое понимание мощности. Одна выражалась в сдвиге по фазе, а другая в искажении формы. Мощность искажения представлена формулой
![]() .
.
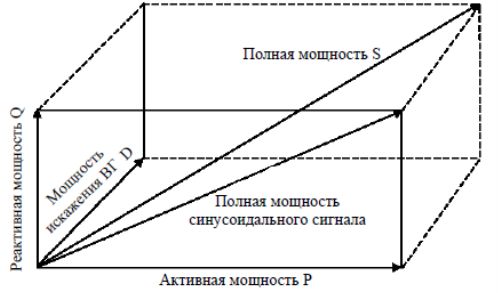
Рис. 1. Геометрическое понимание мощностей
Шклярский Я. Э. в [6] приводит формулу для расчёта мощности искажения через действующие значения токов и напряжений высших гармоник, без определения полной, активной и реактивной мощностей, в случае, когда гармонические составляющие величин заданы. Тогда мощность искажения представлена выражением
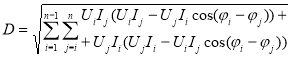 .
.
В диссертации С. Н. Чижмы [5] имеется рисунок 2, на котором наглядно истолкованы понятия активной и реактивной мощности (рисунок 2). В индуктивных элементах происходит отставание тока от напряжения по фазе, в случае, когда ток и напряжение имеют разные знаки. Энергия, запасаемая в индуктивных элементах, совершает колебательные движения. Такую мощность называют реактивной.
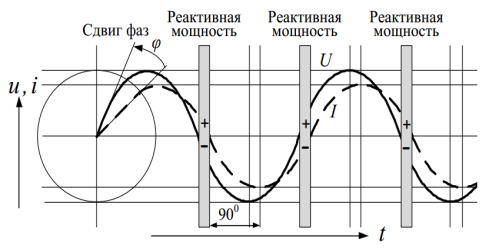
Рис. 2. Истолкование понятий активной и реактивной мощности
Вывод.
Одним из важных параметров в электроэнергетических системах является активная мощность, которая имеет конкретное определение. Поэтому способы определения активной мощности никем не опровергались. Иначе можно говорить о неактивной мощности или реактивной мощности, так как стойкого определения нет. Способов определения реактивной мощности существует много. Именно вопросы определения реактивной мощности являются предметом споров и обсуждений учёных.
Литература:
- ГОСТ 13109–2003. Нормы качества электрической энергии в системах электроснабжения общего назначения [Текст]. — Взамен ГОСТ 13109– 87; введен 1999–01–01. — М.: Госстандарт России, 2010. — 35 с. — (Электрическая энергия. Совместимость технических средств электромагнитная).
- Демирчян, К. С. Теоретические основы электротехники [Текст]: в 3 т. / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровкин, В. Л. Чечурин. — 4-е изд., дополненное для самостоятельного изучения курса. — Питер. — Т. 1. — 2003. — 357 с.
- Маевский О. А. Энергетические показатели вентильных преобразователей [Текст]. -М.: Энергия. — 1978. — 320 с.
- Сулейманов, А. О. Неактивная мощность и её составляющие в элеткроэнергетических системах [Текст]: дис.... канд. тех. наук: 05.14.02 / Алмаз Омурзакович Сулейманов; ГОУ ВПО Томский политехничсекий университет. — Томск, 2009. — 135 с.
- Чижма, С. Н. совершенствование методов и средств контроля качества электроэнергии и составляющих мощности в электроэнергетических системах с тяговой нагрузкой [Текст]: дис.... доктора тех. наук: 05.14.02 / Сергей Николаевич Чижма; Омский государственный университет путей сообщения. — Омск, 2014. — 367 с.
- Шклярский, Я. Э. Влияние гармонического состава тока и напряжения на мощность искажения [Текст] / Я. Э. Шклярский, А. А. Брагин, В. С. Добуш // Электронный научный журнал «Нефтегазовое дело». — 2012. — № 4. — С. 26–32.
- Крогерис, А. Ф. Мощность переменного тока [Текст]: учеб. / А. Ф. Крогерис. — Рига.: Физ.-энерг.ин-т Латв.АН. — 1993. — 294с.







