Особенности расчётов реактивной мощности в несинусоидальных режимах



Согласно ГОСТ 13109–2003 основными параметрами являются колебания напряжения, отклонение частоты, несинусоидальность и несимметрия напряжения. Отсюда следует, что активная и реактивная мощность, а также действующие значения токов и напряжений имеют важное значение при исследовании показателей качества электроэнергии. Именно с определением реактивной мощности возникают трудности, так как нет строгого её определения.

Методы определения составляющих мощности и реактивной мощности.

Буденау впервые ввёл понятие «мощность искажение». Встречается обозначение мощности искажения как «D», а также как «T». По Буденау мощность искажения вычисляется по формуле

.

А. Ф. Крогерис в [1] наглядно изображает составляющие мощности в стандартах США (рисунок 1).

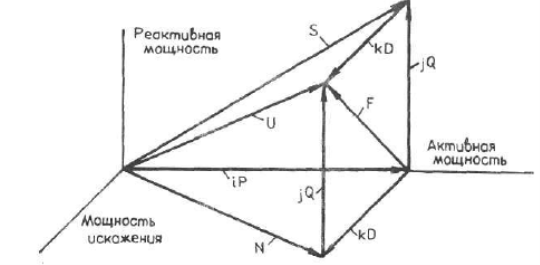
Рис. 1. Составляющие мощности по американским стандартам

Также вопросами составляющих мощности занимались и немецкие учёные. Среди которых выделяет работы Р. Трэгера, который ввёл понятие «мощность взаимного обмена». В немецких нормах при графической интерпретации под S понимают кажущуюся мощность при несинусоидальном режиме, а под S₁- кажущуюся мощность основной гармоники. Соответственно Q и Q₁- это реактивная мощность основной гармоники и при несинусоидальном режиме. Составляющие мощности изображены на рисунке 2.

Рис. 2. Составляющие мощности по немецким стандартам

Можно все существующие методы определения составляющих мощностей разделить на три группы: спектральные, интегральные и энергопотоковые методы. Рассмотрим более подробно каждую группу.

Спектральные методы

Сущность данного метода заключается в том, что составляющие мощности определяются с помощью гармонических составляющих токов и напряжений

Реактивная мощность по Буденау.

Теория Буденаю, состоит в разложении полной мощности на активную, реактивную и мощность искажения. Выражение Буденау представлено формулой

.

Формулы по Буденау получили широкое признание. Неактивная или реактивная мощность присуща сигналу с n-гармониками:

.

Мощность по В. Шеферду и П. Закихани.

Мощность, определяемая в [2] основана на частотном анализе. Он делит гармоники тока и напряжения на общие и необщие гармоники. Реактивная мощность выражена формулой

.

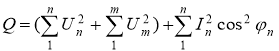Мощность по Шарону.

Определение мощности по Шарону основано также на частотном анализе. Отметим, что у Шарона присутствует термин «кажущийся компонент мощности» которую он определяет в своих трудах. Он развивает исследования формулы и считает, что определении коэффициента мощности в несинусоидальном режиме через функцию косинуса ошибочно. И критикует некоторые моменты теории В. Шеферда и П. Закихани, в частности он считает, что не имеет физического смысла, а лишь математическое понятие. Поэтому он выводит формулу, в которой присутствуют функции гармоник напряжения, тока и функция синуса фазового сдвига.

В [3] реактивную мощность представлена формулой

А. Эмануэль в [4] отметил, что мощность искажения широкого признания не получила и говорит, что необходимо уделить внимание оценке угла смещения для основной гармоники.

Реактивная мощность определяется через основные гармоники напряжения и тока выражением

.

Интегральные методы определения мощности

Реактивная мощность Илиовиси и Маевского [5].

Интегральную формула для расчёта реактивной мощности ввёл М. Илиовиси:

.

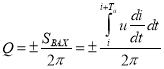Илиовиси и Маевский используют такие понятия, как: мощность сдвига (), мощность искажения () и неактивная мощность ().

Неактивная мощность:

.

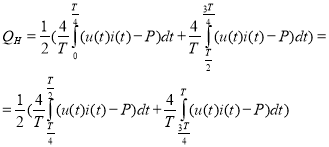Энергопотоковые методы определения мощности

Реактивная мощность Фризе.

Теория Фризе [6] основана на мгновенных значениях токах и напряжениях. Теория состоит в разложении мгновенного тока нагрузки на мгновенный активный ток и мгновенный неактивный (реактивный) ток.

.

Разделение тока на две составляющие происходит в связи с тем, что ток является активной нагрузкой развивает такую же мощность, что и нагрузка, которая исследуется. В итоге если реактивный ток будет скомпенсирован, то будет видна только активная нагрузка.

Полный ток можно определить через среднеквадратичные значения активного и реактивного тока:

.

Реактивную мощность по Фризе всегда положительна и определяется по формуле

.

Мощность по Зарнецкому.

Зарнецкий продолжает в свих работах [7] концепции Фризе. Теория предполагает разделение тока на две составляющие: активный и реактивный ток. Отличием теории от выше описанной, является то, что она предполагает разложение токов на большое количество ортогональных компонент. Реактивная мощность по Зарнецкому, определяется выражением

.

pq- теория.

pq- теория или теория мгновенной мощности используется когда активные компенсаторы применяются для компенсации реактивной мощности в случае наличия составляющих высших гармоник [6]. Активная и реактивная мощность получаются путём преобразования сигналов из трёхфазной системы координат в двухфазную систему координат:

.

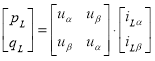Вывод

Сделав обзор существующих методик определения реактивной мощности, отметим, что у каждой методики, теории есть свои преимущества, недостатки. Поэтому вопрос определения мощности является важным и актуальным, и требующим дальнейшего изучения.

Литература:

1. Крогерис, А. Ф. Мощность переменного тока [Текст]: учеб. / А. Ф. Крогерис. — Рига.:Физ.-энерг.ин-т Латв.АН. — 1993. — 294с.
2. Shepherd, W. Suggested definition of reactive power for nonsinusoidal systems / W. Shepherd, P. Zakikhani // Proc. IEE. — 1972. — vol. 119, № 9. — P. 1361–1362.
3. Топорова, Ю. В. Сравнительная характеристика методов определения реактивной мощности [Текст] / Ю. В. Топорова, А. П. Лазуренко // Вісник НТУ «ХПІ». — 2013. — № 17(990). — С. 100–106.
4. Emanuel, A. E. Suggested definition of reactive power in nonsinusoidal systems and reactive-power definitions and power-factor improvement in nonlinear systems / A. E. Emanuel // Proceedings of the Institution of Electrical Engineers. — 1974. — vol. 121, № 7/ — P. 705–706.
5. Kusters, N. On the Definition of Reactive Power Factor of the Supply Systems / N. Kusters, W. Moore // IEEE Trans. Power App. Syst. — 1980. — P. 1845–1854.
6. Чижма, С. Н. совершенствование методов и средств контроля качества электроэнергии и составляющих мощности в электроэнергетических системах с тяговой нагрузкой [Текст]: дис.... доктора тех. наук: 05.14.02 / Сергей Николаевич Чижма; Омский государственный университет путей сообщения. — Омск, 2014. — 367 с.
7. Czarnecki, L. S. Budeanu and fryze: Two frameworks for interpreting power properties of circuits with nonsinusoidal voltages and currents / L. SCzarnecki // Electrical Engineering. — 1997. — vol. 80, № 9. — P. 359–367.