Рассмотрен подход к ускорению расчета динамического напряженно-деформированного состояния с использованием графических сопроцессоров и стандарта OpenCL. Реализована вычислительная программа-прототип расчета для пластины с разными вариантами реализации ядер OpenCL, получены оценки ускорения вычислений, намечены пути повышения производительности.
Ключевые слова: моделирование упругих тел, напряженно-деформированное состояние, динамика систем тел, вычислительное ядро, OpenCL, GPU, FPGA
Введение
Одним из подходов к моделированию динамики технических систем является подход, использующий модель системы как совокупность большого числа тел со связями (далее — многотельные модели или системы — MBS). Примером системы инженерного анализа, использующей такой подход, является система ФРУНД, разработанная и развивающаяся в ВолгГТУ [1]. Наряду с моделированием собственно динамики машин, данная система в своих последних версиях также использует междисциплинарное моделирование, в частности, расчет напряжений и тепловой расчет, сопряженные с моделированием динамики [2]. Одним из вариантов решателя динамического напряженно-деформируемого состояния (НДС) в данной системе является экспериментальный решатель, также базирующийся на многотельном представлении системы и оптимизируемый для максимального использования современных технологий параллельных вычислений и современных архитектур.
В серии работ (в частности [2, 3]) авторами показаны ограничения в масштабируемости решателей MBS системы ФРУНД при использовании декомпозиции расчетных областей и сочетании многопоточных расчетов с распределенными вычислениями. При этом актуальной остается задача сокращения времени моделирования, особенно при выполнении междисциплинарных расчетов. Одним из направлений решения этой задачи является применение ускорителей вычислений, таких, как GPU или FPGA. Для создания переносимых решений, которые можно применять на разных вычислительных архитектурах GPU, CPU, FPGA, MIC, можно воспользоваться стандартом гетерогенных вычислений OpenCL [4].
Основные этапы алгоритма расчета напряжений идеформаций
В математической модели, используемой решателем, каждое упругое тело представляется дискретными твердотельными элементами, расчетная область представлена регулярной ортогональной сеткой в трехмерном пространстве. Каждый такой дискретный элемент имеет форму куба, шесть степеней свободы и от одной до шести связей с соседними элементами.
Движение каждого элемента при действующих в используемом методе допущениях описывается обыкновенным дифференциальным уравнением следующего вида:
,(1)
где
– координаты дискретных элементов, 
– матрица инерции, 
— вектор ускорений твердого тела, входящего в полную динамическую модель, 
— силы стабилизации. Функция 
описывает силы между дискретными элементами. Случайные возмущения, передаваемые от динамической модели, могут вызывать смещение дискретных элементов, поэтому для их привязки к опорному телу введены силы стабилизации.
Численное интегрирование системы обыкновенных дифференциальных уравнений (1) явным методом Рунге-Кутты 4-го порядка точности и обновление правых частей уравнений являются основными элементами расчета напряженно-деформированного состояния. Подробнее основные этапы расчета динамического НДС с использованием дискретных элементов рассмотрены, например, в [3, 5].
Для переноса решателя на GPU и впоследствии на FPGA был разработан упрощенный прототип, в котором рассматривается простое тело — упругая пластина, представленная большим числом (миллион) дискретных элементов.
В прототипе были опущены многие промежуточные операции, не занимающие значительного времени, но выполняющиеся в реальном решателе. На рисунках 1 и 2 показаны алгоритмы работы прототипа. На рисунке 1 — реализация метода Рунге-Кутты с перерасчетом правых частей дифференциальных уравнений, а на рисунке 2 — собственно перерасчет правых частей.
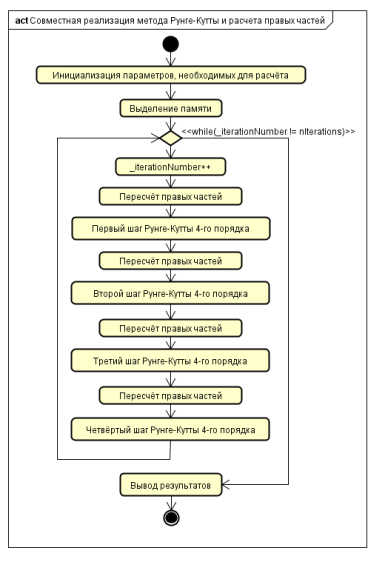
Рис. 1. Алгоритм совместной реализации метода Рунге-Кутты и расчета правых частей
Проведенное профилирование программы-прототипа, выполняющего последовательную версию расчета, показало, что большую часть времени решения (почти 67 %) занимает расчет правых частей уравнений, при этом само численное интегрирование и пересчет матриц поворота (требуются для преобразования координат) выполняются гораздо быстрее (13 %). Значительную часть времени (порядка 20 %) занимает выполнение вспомогательных операций.
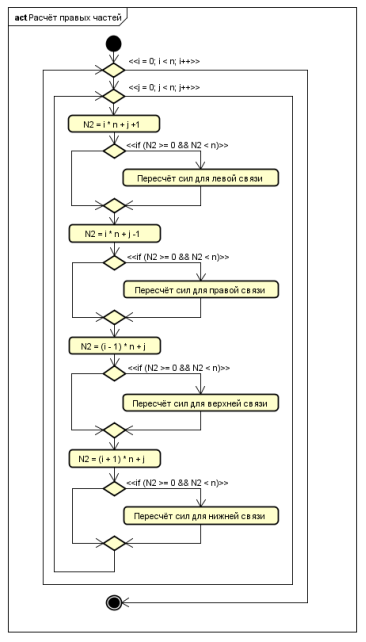
Рис. 2. Алгоритм функции пересчёта правых частей
Последовательная часть программы при расчете для пластины, представленной 1 миллионом дискретных элементов, составляет примерно α = 40 %. По закону Амдала, при количестве потоков 
ускорение приблизительно равно:
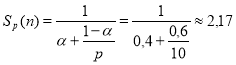(2)
Необходимо отметить, что приведенная выше оценка (α = 40 %) относится к расчету НДС в целом.
Варианты параллельных алгоритмов, использующих ядра OpenCL иоценки получаемого ускорения
Учитывая полученные оценки, можно сделать вывод, что в первую очередь следует оптимизировать модуль расчета правых частей, так как он является самым объемным и вычислительно сложным.
Другие элементы расчета также требуют значительных, хоть и меньших, временных затрат, следовательно, получив ускорение на расчете правых частей, следующим шагом необходимо оптимизировать и их.
Расчет правых частей уравнения реализуется следующим образом: сначала второе тело из пары переводится в систему координат первого путем умножения справа на соответствующую матрицу поворота; затем, уже в одной системе координат, рассчитываются линейные и угловые деформации и сдвиги, возникшие в связях под действием приложенной силы. Полученные приращения по всем направлениям, переведенные в глобальную систему координат, характеризуют НДС тела в данный момент времени. Распараллеливание расчета осуществляется путем разделения на потоки расчета для деформаций каждой пары узлов.
Первоначально в ядро (kernel) OpenCL был выделена часть расчёта правых частей, отвечающая за расчёт деформации для пары элементов, так как эта функция вызывается наибольшее количество раз. Ускорение, которого удалось достичь этим подходом, было незначительным (порядка 1.1 раза).
Затем в ядро OpenCL был выделен расчёт правых частей уравнений в целом, так как эта часть вычислений занимает наибольшую долю времени. Здесь потребовалось выделить отдельные массивы для каждого рабочего потока (work-item’ов OpenCL). Это приводит к большим тратам времени на пересылку данных из хостового приложения в устройство. При этом, однако, сам расчет на ядрах для относительно современных GPU происходит заметно быстрее, чем на CPU.
Замер времени выполнения версии алгоритма расчета правых частей уравнений, реализованного на OpenCL, показал, что даже с учётом пересылок данных возможно ускорение по сравнению с расчетом на одном ядре CPU до 1.4 раз на графическом ускорителе NVidiaGeForceGT520M и свыше 6 раз на GPU-ускорителе NVidiaTESLAK20 (таблица 1). Если же не учитывать пересылку данных, то ускорение собственно вычислений может достигать 16 раз (для K20). Последнее замечание могло бы иметь практический аспект при использовании графических ядер, интегрированных с ядрами CPU.
Таблица 1
Ускорение расчета для прототипа решателя динамического НДС при использовании ядер OpenCL на GPU по сравнению срасчетом на одном ядре CPU
|
Модель GPUNVidia |
Для всего расчета |
Для расчета правых частей |
Для расчета на ядрах GPU без учета времени пересылки |
|
GeForce GT520M |
1,2 |
1,38 |
1,79 |
|
TESLAK20 |
1,2 |
6,36 |
15,9 |
В целом, конечно, полученные на данном этапе результаты далеки от ожидаемых. В частности, для схожей (но более простой) задачи расчета теплового режима ранее были получены оценки ускорения при расчете на GPU до 20 раз [6] (в том случае использована технология CUDA, а не OpenCL, но выбор технологии не может объяснить такую существенную разницу в относительной производительности).
Можно отметить следующие причины относительно невысокого прироста производительности:
интенсивный обмен данными между хостовой частью программы и ядрами, выполняемыми на GPU;
неоптимизированный алгоритм вычислений, не учитывающий возможности векторизации вычислений на GPU, оптимизацию использования разных типов памяти;
необходимо ускорить также выполнение прочих операций в общем алгоритме расчета (интегрирование ОДУ, вспомогательные операции).
Вместе с тем показана принципиальная возможность ускорить вычисления с помощью GPU, используя для выгрузки интенсивных вычислений на сопроцессор стандарт OpenCL. В дальнейшем предполагается улучшить полученные результаты для GPU, а также провести эксперименты по выполнению аналогичного алгоритма на ПЛИС (FPGA) с поддержкой OpenCL как входного языка разработки ядер, размещаемых в ПЛИС. Заметим, что в связи со скорым выпуском ядер FPGA, интегрируемых с CPU (в семействе процессоров IntelXeonSkylake), проблема задержки на пересылки данных может быть в значительной степени нивелирована.
Выводы
Разработанный параллельный алгоритм расчёта правых частей системы ОДУ на GPU с использованием OpenCL показал возможность ускорения вычислений правых частей системы дифференциальных уравнений при решении задачи напряженно-деформированного состояния от 1.5 до 6 раз по сравнению с версией расчета, выполняемого на центральном процессоре. Основные накладные расходы связаны с пересылкой большого количества данных и требуют, в дальнейшем, уменьшения за счёт оптимизации работы с памятью. При реализации ядер GPU или FPGA в одном корпусе с ядрами CPU (как в решениях AMD, либо в готовящихся решениях Intel) эта проблема отойдет на второй план из-за увеличения пропускной способности при передаче на ядро сопроцессора на 1–2 порядка.
Исследование выполнено при финансовой поддержке РФФИ в рамках научных проектов №№ 16-07-00534, 15-01-04577, 15-07-06254, при финансовой поддержке РФФИ и Администрации Волгоградской области в рамках научного проекта № 16-47-340385.
Литература:
1. Горобцов, А. С. Представление подвески легкового транспортного средства в системе моделирования «ФРУНД» / А. С. Горобцов, Ан.В. Подзоров // Изв. ВолгГТУ. Серия «Актуальные проблемы управления, вычислительной техники и информатики в технических системах»: межвуз. сб. науч. ст. / ВолгГТУ. — Волгоград, 2008. — Вып. 4, № 2. — C. 8–10.
2. Concurrent simulation of multibody systems coupled with stress-strain and heat transfer solvers / В. В. Гетманский, А. С. Горобцов, Е. С. Сергеев, Т. Д. Измайлов, О. В. Шаповалов// Journal of Computational Science. — 2012. — Vol. 3, Iss. 6. — C. 492–497. — Англ.
3. Гетманский, В. В. Распараллеливание расчёта напряжённо-деформированного состояния тела в многотельной модели методом декомпозиции расчётной области / В. В. Гетманский, А. С. Горобцов, Т. Д. Измайлов // Известия ВолгГТУ. Серия «Актуальные проблемы управления, вычислительной техники и информатики в технических системах». Вып. 16: межвуз. сб. науч. ст. / ВолгГТУ. — № 8 (111), 2013. — C. 5–10.
4. OpenCL — The open standard for parallel programming of heterogeneous systems [Электронный ресурс]. Режим доступа: https://www.khronos.org/opencl/.
5. Мовчан, Е. О. Векторизация алгоритмов для моделирования динамики систем тел / Е. О. Мовчан, В. В. Гетманский, А. Е. Андреев // Суперкомпьютерные технологии (СКТ–2016): матер. 4-й всерос. науч.-техн. конф. (пос. Дивноморское, г. Геленджик, 19–24 сент. 2016 г.). В 2 т. Т. 1 / РФФИ, Южный науч. центр РАН, Южный федерал. ун-т [и др.]. — Ростов-на-Дону, 2016. — C. 179–183.
6. Гетманский, В. В. Вычислительно эффективный метод расчёта теплопередачи при анализе динамики механической системы / В. В. Гетманский, А. С. Горобцов, В. О. Лаптева // Прикладные задачи математики: матер. XXII междунар. науч.-техн. конф. (Севастополь, 15–19 сент. 2014 г.) / Севастопольский нац. техн. ун-т (СевНТУ). — Севастополь, 2014. — C. 65–68.
