Приведены сведения по динамике грузоподъемного крана. Даны рекомендации по повышению устойчивости грузоподъемного крана.
Ключевые слова: динамика, подъема, груз, нагрузка, упругость, крюк, масса, усилие, отрыв,оборудования
Динамика колебательного процесса подъемного механизма стрелового крана рассматривается как система состоящая из массы груза, массы крана, массы ротора электродвигателя и элементов подъемного механизма, связанных между собой упругими звеньями и жесткостями подъемных канатов и металлоконструкции крана. В работе [1] сделано допущение, что упругость металлоконструкции значительно выше упругости каната. Эта обоснованность подтверждается экспериментально. При указанных допущениях подъем груза производится путем выбора слабины каната, упругой деформации всех элементов конструкции и отрыве с места.
Максимальные динамические нагрузки появляются при отрыве груза.
Процесс подъема груза механизмом подъема стоит из:
– выборки зазоров в канате;
– отрыва груза от земли;
– движения груза в установившемся режиме работы.
На рисунке 1 приведена двухмассовая динамическая схема подъема груза краном.
Груз поднимается поступательно в режиме неустановившегося движения. На первом этапе выбирается зазор Δ.
Процесс выборки зазоров описывается системой уравнений
,
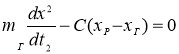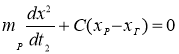(1)
.
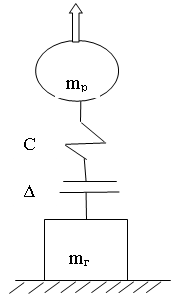
Рис. 1. Двухмассовая динамическая схема подъема груза
mг, масса груза и грузозахватного органа; mр — приведенная масса вращающихся частей привода; Δ — зазоры в механизме;
С — коэффициент упругости полиспаста;
На втором этапе в упругой связи возникает нагрузка F
,
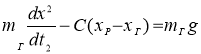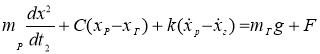(2)
где xг, xр — перемещение груза и ротора привода; F — избыточная сила механизма.
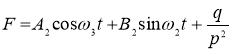,(3)
; 
.
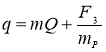Избыточная сила механизма в виде синусоидальной составляющей амплитуды создает наиболее тяжелый нагрузочный режим. Появление синусоидальной составляющей не только увеличивает наибольшую динамическую нагрузку, но и может привести к качественным изменениям в характере движения оборудования крана. Для снижения динамической нагрузки требуется гашение колебаний в системе [2]. При введении системы гашения наибольшая нагрузка упругого ускоренного подхвата определяется
Р =abs(exp(-кu)Аsin(ωu))(4)
где ω — круговая частота колебаний; u — время протекания процесса.
Наибольшая нагрузка равномерного подхвата
(5)
где V — скорость подъема груза.
Для кранов, у которых соотношение массmр >= тг формула определения наибольшей нагрузки
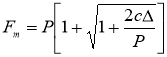(6)
При определении нагрузки несостоявшегося подъема, такая нагрузка обычно аварийная, уравнение движения в этом случае
.(7)
где mк — масса крана; mг — масса груза; с жестокость полиспаста; x — перемещение груза.
Обозначив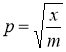 
и 
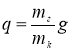(8)
Имеем решение этого уравнения
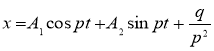
.(9)
Максимальное усилие подъема будет при 
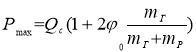,(10)
где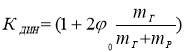 
.
Этим выражением определяется динамическая загрузка как каната так и любого упругого элемента механизма подъема [3].
При подъеме груза с учетом податливости металлоконструкции стрелы крана динамическая модель системы приведена на рисунке 2.
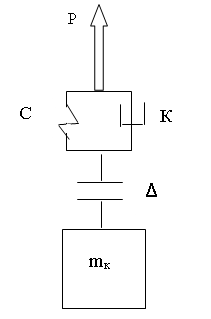
Рис. 2. Динамическая модель рабочего оборудования крана
При анализе динамики колебательного процесса, происходящего при подъеме груза с учетом податливости металлоконструкции приняты слудующие допущения.
- Масса крана и груза рассматривается как общая масса.
- Упругость металлоконструкции значительно больше упругости канатов и привода механизма.
Обоснованность таких допущений подтверждается экспериментально [4].
Подъем груза при принятых допущениях производится следующим образом.
Первый этап. После включения двигателя происходит выборка зазоров в канате.
Второй этап. Происходит упругая деформация всех элементов конструкции. Это продолжается пока усилие на крюке не станет равным грузоподъемности.
Третий этап. Подъем груза.
За обобщенную координату X принимается перемещение Xк массы крана mk, обладающей жесткостью kk.
Первый этап описывается уравнениями
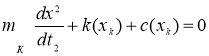,(11)
.
На втором этапе уравнение подъема груза имеет вид
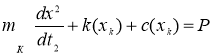.(12)
В момент отрыва груза усилие подъема определится по уравнению
Р =abs(exp(-u)Аsin(ω u))(13)
где ω — частота колебаний груза; `u — время отрыва груза.
На третьем этапе усилие подъема груза равно грузоподъемности. Движение груза описывается уравнением гармонических колебаний. Уравнение подъема груза имеет вид
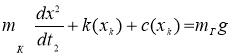.(14)
Полная нагрузка на крюк равна сумме статической и динамической
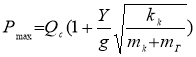.(15)
где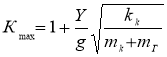 
Выводы
Грузовая устойчивость грузоподъемного крана в области граничного равновесия обеспечивается рациональным сочетанием динамических свойств привода, полиспаста, металлоконструкции стрелы и времени срабатывания тормозной системы.
Литература:
- Емельянов Р. Т., Прокопьев А. П., Турышева Е. С., Постоев П. А. Реализация нейросетевого контроллера для управления организационно-технологическим комплексом // Вестник Сибирского аэрокосмического университета. 2011. Вып. 1. С. 20–24.
- Емельянов Р. Т, Спирин Е. С., Кириллов К. В., Циганкова А. В. Исследование автоматической системы управления с пропорционально-интегрально-дифференциальным регулированием// Вестник Красноярского государственного аграрного университета. № 10. 2013. с. 243–247
- Емельянов Р. Т., Султанов Н. С., Закурдаев А. В., Скурихин Л. В. Моделирование динамики регулируемого гидромотора // Вестник Красноярского государственного аграрного университета, № 8, 2014. с.181–185
- Терехова, И. И. Управление системой устойчивости башенного крана/ И. И. Терехова, Р. Т. Емельянов. // Совершенствование машин и ресурсосберегающих технологий: Межвуз. сб. науч. ст.- КФ Иркутский ГУПС, 2005. С. 36–44.
