Рассмотрены особенности внесения жидкого консерванта в травяную ленту при подборе травы в рулоны. Для повышения равномерности внесения разработан метод и алгоритм позволяющий определить оптимальные перекрытия факелов распыла консерванта с соседними распылителями. Приведены расчеты для конкретных экспериментальных данных.
Ключевые слова: корма, консервант, форсунки, равномерность
При внесении жидких консервантов в травяные рулонные корма наиболее важным показателем валяется неравномерность их распределения внесения по ширине травяной ленты. Снижения неравномерности распределения консерванта, до допустимой агротребованиями величины, можно достигнуть путем изменения шага расстановки форсунок по ширине травяной ленты на транспортере, подающим траву в прессовальную камеру рулонного пресс-подборщика [3,5].
Распределение консерванта по ширине каждой из форсунок представляется некоторой выпуклой кривой. При совместной работе форсунок, для повышения равномерности внесения консерванта, зоны их работы (кривые распределения консерванта) перекрываются путем сдвига навстречу соседних форсунок.
Кривая распределения консерванта по ширине одной форсункой f(х)может быть описана аналитически.
Если соседняя слева, такая же форсунка, даёт распределение консерванта, описываемое кривой f5(х), правая часть которой на участке Δxнакладывается на кривую f1(х), то на данном участке распределение консерванта будет определяться суммарной кривой: ![]() при 0 < х < Δx.
при 0 < х < Δx.
В идеале перекрытие должно быть таким, чтобы соседние кривые с наименьшей погрешностью покрывали площадь ![]() , т. е. необходимо минимизировать уравнение:
, т. е. необходимо минимизировать уравнение:
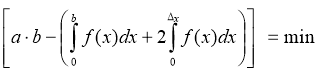 (1)
(1)
В уравнении (1) необходимо определить значение Δx, обеспечивающее минимальное значение разности.
В уравнении (1) есть постоянные составляющие, которые можно определить заранее.
Обозначим:
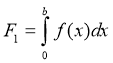 ,
, ![]() (2)
(2)
Тогда уравнение (1) примет вид:
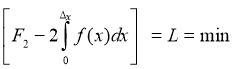 (3)
(3)
Для определения Δx из уравнения (3) необходимо представить в алгебраическом виде для конкретного вида уравнения функции f(х).
Как показали экспериментальные исследования распылителей, кривые распределения массы консерванта по ширине хорошо описывается полиномом второго порядка:
![]() (4)
(4)
Подставляя (4) в уравнения (2) получим формулу для определения ![]()
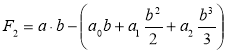 (5)
(5)
Подставим уравнение (4) в формулу (3), определим интеграл, и подставим пределы интегрирования. После выполнения операции интегрирования и упрощения, получим уравнение:
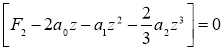 , (6)
, (6)
где z = Δx.
В уравнении (6) предельное значение в общем виде «min», заменено на конкретное значение «ноль», так как сумма ![]() должна покрывать всю площадь
должна покрывать всю площадь ![]() .
.
Уравнение (6) можно решать в системе Excel методом «Подбор параметра» [1].
На рисунке 1 приведены результаты подбора теоретической кривой к экспериментальным данным исследования распылителя.
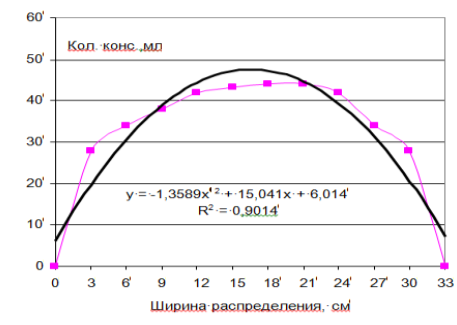
Рис. 1. Результаты аппроксимации полиномом второго порядка экспериментальных данных распределения консерванта форсункой
Полученное уравнение имеет вид:
![]() (7)
(7)
и описывает экспериментальные данные с высоким коэффициентом корреляции (r = 0,92).
Ширина факела распределения составляет 33 см (b = 33), высота — 48 см (a = 48).
Подставляя значения a, b и коэффициенты уравнения (7) в (5) получим F2 = 705,2.
Подставляя значение F2 и коэффициенты уравнения (7) в (6) получим уравнение:
![]() (8)
(8)
Решение уравнения (8) методом «Подбор параметра» дало следующее значение:
z = Δx = 9,786, то есть соседние распылители необходимо сдвинуть навстречу друг другу на 3, 9 см.
На рисунке 2 приведены результаты расчетов распределения консерванта при реализации данного сдвига распылителей.
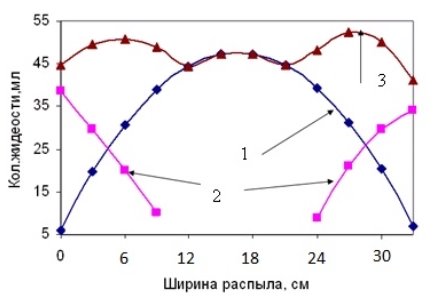
Рис. 2. Результаты аппроксимации полиномом второго порядка экспериментальных данных распределения консерванта форсункой: 1 — кривая распределения консерванта от одной форсунки; 2 — кривые распределения консерванта от соседних форсунок; 3 — суммарная кривая распределения консерванта от трех форсунок
Выводы:
- Для повышения равномерности внесения консервантов в травяную массу при формировании рулонов необходимо расставлять распылители с перекрытием их факелов распределения.
- Распределение консерванта одной форсункой имеет колоколообразную образную форму и с высокой точностью аппроксимируется полиномом второго порядка.
- Для определения оптимального перекрытия разработаны метод построения математической модели и алгоритм расчета величины перекрытия.
- Решение задачи выполняется в системе Excel по опции «Подбор параметра».
Литература:
- Валге А. М. Использование систем Excel и MathCAD при проведении исследований по механизации сельскохозяйственного производства (Методическое пособие) / А. М. Валге, ГНУ СЗНИИМЭСХ Россельхозакадемии. — СПб., 2013. — 200 с.
- Валге А. М., Использование информационных технологий при проектировании процессов производства продукции растениеводства / Валге А. М., Папушин Э. А., Пакскина Е. Г.// Механизация и электрификация сельского хозяйства. 2012. № 3. С. 17–18.
- Юнин В. А. Интенсификация кормопроизводства в условия Северо-Западного региона / Юнин В. А., Зыков А. В., Кузнецов Н. Н. // В сборнике: Технические науки в России и за рубежом Материалы V Международной научной конференции. 2016. С. 82–85.
- Валге А. М. Оптимизация транспортных потоков при заготовке кормов из трав / Валге А. М., Папушин Э. А., Зыков А. В., Веденский Н. В. // Технологии и технические средства механизированного производства продукции растениеводства и животноводства. 2015. № 87. С. 116–122.
- Юнин В. А. Оценки эффективности применения консервантов при производстве кормов в условиях Северо-Западного региона / Юнин В. А., Зыков А. В.// В сборнике: Современные тенденции технических наук Материалы IV Международной научной конференции. 2015. С. 121–123.







