Ключевые слова: отложения, теплообменник,трубный пучок
Испарительный контур экстракционной фосфорной кислоты, применяемый на АО «ФосАгро-Череповец», состоит из бака нагрева и двух вакуум-испарителей. Бак нагрева представляет собой ёмкость прямоугольного сечения, в которую вмонтирована батарея из 40 нагревательных коллекторов. Каждый коллектор состоит из двух вертикальных труб, соединённых горизонтальными трубами, причём каждый следующий элемент смещён по вертикали от предыдущего. Таким образом образуется шахматный пучок труб. Теплоносителем является пар низкого давления. В процессе работы происходит быстрое зарастание пучка труб отложениями сульфата кальция, что приводит к снижению теплового потока от теплоносителя к кислоте. В частности, это происходит из-за уменьшения коэффициента теплоотдачи от греющей поверхности к потоку фосфорной кислоты. Поэтому данная статья посвящена исследованию зависимости коэффициента теплоотдачи пучка труб от толщины отложений.
Согласно [1] коэффициент теплоотдачи α пучка труб с десятью и более рядами труб можно определить из соотношения:
(1)
где 
– характерная длина трубы, м
(2)
– коэффициент теплопроводности кислоты, Вт/(м∙˚С)
– число Нуссельта для пучка труб
(3)
Где, соответственно
– число Нуссельта для одиночной трубы, 
– коэффициент структуры для шахматного пучка труб, K – коэффициент, учитывающий зависимость свойств жидкости от температуры.
При нагревании жидкости
(4)
Здесь Pr – число Прадтля при средней температуре Tb, Prw – число Прадтля при температуре стенки Tw.
(5)
Где 
– температура на входе в пучок труб, ˚С
– температура на выходе из пучка труб, ˚С
Число Нуссельта для одиночной трубы зависит от чисел Нуссельта для ламинарного и турбулентного слоёв:
(6)
Причем
(7)
(8)
Где 
– число Рейнольдса:
(9)
Здесь 
– скорость жидкости в свободном от труб сечении, м/с, 
– доля пустот,
– кинематический коэффициент вязкости жидкости, м2/с, 
– средняя скорость в зазоре между двумя соседними радами труб.
Определим данные параметры для условий нашей задачи. Для этого необходимо ввести понятия безразмерных поперечного (
) и продольного (
) шагов трубного пучка. Размеры d, s1 и s2 показаны на рисунке 1.
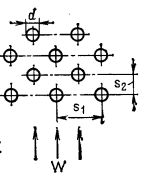
Рис. 1 Шахматный пучок труб
- Доля пустот напрямую зависит от шагов a и b.
если 
если 
В нашем случае, будет применяться формула 
- Коэффициент структуры для шахматного пучка труб.
(10)
Необходимо отметить тот факт, что коэффициент теплоотдачи увеличивается от первого ряда трубного пучка к пятому и остается неизменным в последующих рядах. Поэтому при расчете средних чисел Нуссельта для пучка из десяти и более рядов труб нет необходимости учитывать более низкие коэффициенты теплоотдачи первых рядов.
Исходя из вышеизложенного можно вывести формулу нахождения коэффициента теплоотдачи от шахматного пучка труб
(11)
Подставляя в формулу данные их приведенных ранее формул, получим формулу зависимости коэффициента теплоотдачи пучка труб от диаметра чистой трубы, то есть трубы в начальный момент времени:
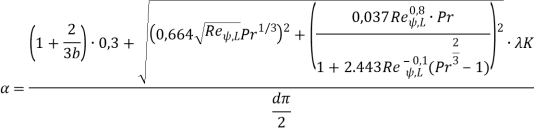(12)
С увеличением времени диаметр d увеличивается по формуле
(13)
Здесь 
– толщина отложений из раствора фосфорной кислоты, увеличивающаяся во времени.
Формулы зависимости толщины от времени изучались различными авторами. В работах [2, 3] приведены наиболее современные теории кинетики роста отложений.
Подставляя (13) в (12) получим искомую зависимость коэффициента теплоотдачи пучка труб от толщины отложений
(14)
Литература:
- Справочник по теплообменникам: В 2-х т. Т. 1 / С 74 Пер. с англ., под ред. О. Г. Мартыненко и др.— М.: Энергоатомиздат, 1987. — 560 с.: ил.
- Behbahani R. M., Muller-Steinhagen H., Jamialahmadi M. Investigation of Scale Formation in Heat Exchangers of Phosphoric Acid Evaporator Plants // The canadian journal of chemical engineering. — 2006. — № 84. — pp. 189–197.
- Ishiyama E.M., Paterson, W.R., Wilson, D. I. Exploration of alternative models for the aging of fouling deposits // AIChE Journal— 2011. — № 11. — pp. 3199–3209.
