В статье рассматривается задача управления перемещением квадрокоптера вдоль координатной оси. За счет допустимых преобразований математическая модель приводится к системе из двух подсистем канонического вида. С помощью метода нелинейной стабилизации находится стабилизирующее управление. Выполнено численное моделирование замкнутой управлением системы в среде MATLAB.
Ключевые слова: стабилизирующее управление, метод нелинейной стабилизации, квадрокоптер
Квадрокоптер — беспилотный летательный аппарат с четырьмя несущими винтами, причем два винта, расположенных диагонально, вращаются в одну сторону, а остальные два — в другую. Особенность квадрокоптера состоит в том, что он имеет шесть степеней свободы (три из которых — это координаты аппарата в неподвижной системе координат, остальные три — это угловые координаты, связанные с подвижной системой координат), а управляющих параметров всего четыре — угловые скорости вращения винтов.
Математическая модель квадрокоптера (математическая модель движения твердого тела в углах Крылова) имеет следующий вид [1]:
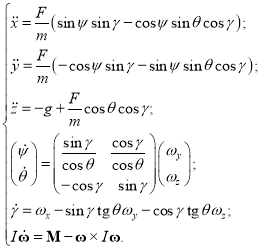 (1)
(1)
где ![]() — масса твердого тела;
— масса твердого тела; ![]() — ускорение свободного падения;
— ускорение свободного падения; ![]() — матрица инерции;
— матрица инерции; ![]() — координаты центра масс (в НСК);
— координаты центра масс (в НСК); ![]() — суммарная сила тяги (по модулю) четырех винтов;
— суммарная сила тяги (по модулю) четырех винтов; ![]() — угол рыскания;
— угол рыскания; ![]() — угол тангажа;
— угол тангажа; ![]() — угол крена;
— угол крена; ![]() — компоненты вектора угловой скорости
— компоненты вектора угловой скорости ![]() (в ПСК);
(в ПСК); ![]() — суммарный момент сил.
— суммарный момент сил.
Рассмотрим перемещение квадрокоптера вдоль одной из координатных осей НСК, например, вдоль оси Y. Считаем, что координаты по остальным осям X и Z остаются постоянными и равными нулю. Тогда, углы рыскания ![]() и тангажа
и тангажа ![]() , а также угловые скорости
, а также угловые скорости ![]() и
и ![]() тождественно равны нулю. В системе (1) полагаем
тождественно равны нулю. В системе (1) полагаем
![]()
где ![]() — нулевой вектор-столбец. Эти условия налагают на поведение системы следующие ограничения:
— нулевой вектор-столбец. Эти условия налагают на поведение системы следующие ограничения:
![]() (2)
(2)
а уравнения движения принимают следующий вид:
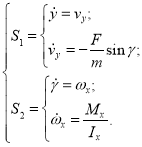 (3)
(3)
В этой системе два параметра, связанных с управлением: сила тяги винтов F и составляющая момента сил ![]() .
.
Для подсистемы S1 рассмотрим отклонение ![]() , где
, где ![]() — требуемое значение на оси Y. Введем обозначения:
— требуемое значение на оси Y. Введем обозначения: ![]() и
и ![]() Подсистема S1 — система канонического вида, в переменных
Подсистема S1 — система канонического вида, в переменных ![]() записывается следующим образом:
записывается следующим образом:
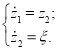
Управление ![]() выберем таким образом, чтобы отклонение
выберем таким образом, чтобы отклонение ![]() асимптотически стремилось к нулю:
асимптотически стремилось к нулю:
![]()
где ![]() и
и ![]() — некоторые положительные константы. С другой стороны,
— некоторые положительные константы. С другой стороны,
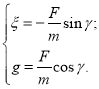
Из этой системы нетрудно выразить угол крена: ![]()
Для подсистемы S2 рассмотрим отклонение ![]() , где
, где ![]() — требуемый угол крена квадрокоптера. Введем обозначение:
— требуемый угол крена квадрокоптера. Введем обозначение: ![]() , причем
, причем
Подсистема S2 — система канонического вида, в переменных ![]() записывается следующим образом:
записывается следующим образом:
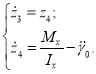
Управление ![]() выберем таким образом, чтобы отклонение
выберем таким образом, чтобы отклонение ![]() асимптотически стремилось к нулю:
асимптотически стремилось к нулю:
![]() (5)
(5)
где ![]() и
и ![]() — некоторые положительные константы, причем
— некоторые положительные константы, причем
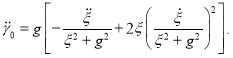 (6)
(6)
Таким образом, используя выражения (2) и (5), можно однозначно определить силу тяги винтов ![]() и составляющую момента
и составляющую момента ![]() для системы (3). Заметим, что полученные управления можно подставить и в исходную систему (1) — выражения (2) и (5) будут гарантировать перемещение квадрокоптера вдоль оси Y.
для системы (3). Заметим, что полученные управления можно подставить и в исходную систему (1) — выражения (2) и (5) будут гарантировать перемещение квадрокоптера вдоль оси Y.
Результаты численного моделирования, выполненного в среде MATLAB, для системы (1) с управлениями (2) и (5) представлены на рис. 1–6 при следующих значениях параметров рассматриваемой системы и управления [2]:
![]()
![]()
Начальное положение квадрокоптера —
Начальные условия: ![]()
По результатам моделирования (см. рис. 1–6) можно сделать вывод о работоспособности построенного стабилизирующего управления. Аналогично можно решить задачу перемещения квадрокоптера вдоль оси X. Заметим, что поворотом неподвижной системы координат относительно оси Z, всегда можно добиться совпадения некоторой прямолинейной траектории с осью Y.
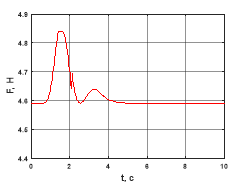
Рис. 1. Сила тяги ![]()
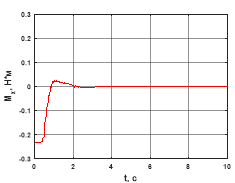
Рис. 2. Составляющая момента сил ![]()
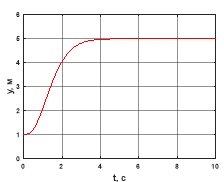
Рис. 3. Координата Y
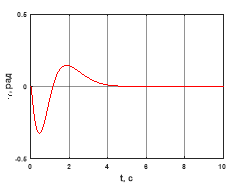
Рис. 4. Угол крена
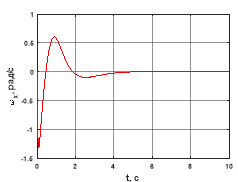
Рис. 5. Угловая скорость ![]()
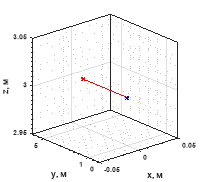
Рис. 6. 3D-траектория квадрокоптера
Литература:
- Канатников А. Н., Акопян К. Р. Управление плоским движением квадрокоптера // Математика и математическое моделирование. МГТУ им. Н. Э. Баумана. Электрон. журн. 2015. № 2. С. 23–36. DOI: 10.7463/mathm.0215.0789477
- Tayebi A., McGilvray S. Attitude stabilization of four-rotor aerial robot // 43rd IEEE Conference on Decision and Control. 2004. Vol.2. P. 1216–1221







