В статье рассматривается нелинейная экономическая модель бизнес-цикла Николаса Калдора. Дается строгое обоснование применения теоремы Пуанкаре-Бендиксона о существовании периодической траектории. Приводятся результаты численного моделирования.
Ключевые слова: модель Калдора, теорема Пуанкаре-Бендиксона, периодическая траектория
В последние годы нелинейные модели экономической динамики привлекают внимание многих исследователей, как экономистов, так и математиков. С одной стороны этот интерес обусловлен практической необходимостью, поскольку во многих ситуациях математическое моделирование является единственным средством исследования сложных экономических процессов. С другой стороны, моделирование экономических систем часто приводит к постановкам новых содержательных математических задач. Особый интерес представляет изучение нелинейных моделей экономической динамики, способных генерировать циклические движения, которые могут интерпретироваться, как периодически повторяющиеся кризисные явления.
Одной из таких экономических моделей, в которой возможна циклическая динамика, является известная модель бизнес-цикла Николаса Калдора, предложенная в 40-е годы ХХ века (см. [1]). Данная модель описывает динамику национального дохода и основных производственных фондов (капитала) абстрактной экономики в зависимости от заданных функций инвестиций и сбережений. Основная идея модели Калдора состоит в том, что возникающие в экономике циклы могут иметь внутреннюю (эндогенную) природу, связанную с нелинейностями, присущими рассматриваемым экономическим процессам.
В статье обосновывается применение теоремы Пуанкаре-Бендиксона (см. [2]) о существовании периодических траекторий к модифицированной версии модели Калдора. Приведены результаты численного моделирования в среде MAPLE.
Модифицированная модель Калдора
Рассмотрим следующую модификацию модели Калдора:
(1)
здесь 
и 
— величины национального дохода и основных производственных фондов (капитала) в момент 
, 
— поправочный коэффициент, характеризующий скорость реакции системы, 
— норма амортизации основных фондов, 
и 
— заданные функции инвестиций и сбережений.
Будем считать, что функции инвестиций
и сбережений 
имеют следующий вид:
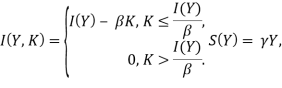(2)
где 
, 
и 
— такая положительная дважды непрерывно-дифференцируемая функция, что 
, 
, 
и существует такое 
, что 
если 
и 
если 
. Заметим, что данная модель отличается как от исходной модели Калдора (см. [1]), так и от ее версии, рассмотренной в работе [3]. В нашем случае функция сбережений не зависит от фазовой переменной 
, а зависит только от переменной 
. Кроме того, функция инвестиций 
— неотрицательная (см. (2)).
Известно (см. [3]), что в общем случае система (1) может иметь от одного до трех положений равновесия, которые могут быть как устойчивыми, так и неустойчивыми. В некоторых случаях система (1) может демонстрировать циклические движения. Такое поведение траекторий системы можно интерпретировать, как возникающие в экономике циклы экономического подъема с последующими спадами (т. е. кризисами).
Определим открытое множество 
и кривую 
следующим образом:
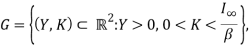(3)
(4)
Очевидно, что кривая 
делит множество 
на две части:
Заметим, что в силу непрерывности функции инвестиций (см. (2)) и стандартной теоремы существования решения дифференциального уравнения (см. [2]), для любого начального состояния 
соответствующее решение 
системы (1) с начальными условиями 
существует на некотором ненулевом интервале 
. Поскольку во внутренности множества 
и во множестве 
функция непрерывно дифференцируема, а произвольное решение системы (1) можете пересекать кривую только в изолированные моменты времени (данный факт легко проверяется непосредственно), то для любого начального состояния решение соответствующей задачи Коши единственно. Далее, в силу ограниченности функции инвестиций все траектории системы (1) с начальным состоянием определены на бесконечном интервале 
.
Пусть 
— любое число, превосходящее максимальный корень уравнения 
. Обозначим через 
прямоугольник
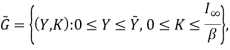
а через 
, 
, 
и 
— его стороны:
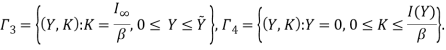
Кривая (см. (4)) делит прямоугольник на две части:
В множестве 
система (1) имеет вид
(5)
Соответственно, в множестве 
система (1) имеет вид
(6)
Следующий результат обосновывает применение теоремы Пуанкаре-Бендиксона к системе (1) с функцией инвестиций (2).
Теорема 1. Для любого сколь угодно малого
существует такая непрерывная замкнутая кривая без самопересечений 
, отстоящая от границы множества не более чем на 
(в хаусдорфовой метрике), что в каждой точке 
векторное поле системы (1) направлено во внутрь множества .
Доказательство. Непосредственно проверяется, что на сторонах , и прямоугольника векторное поле системы (1) направлено во внутрь множества . В точке 
правая часть системы (1) принимает значение 
. Выберем произвольное . Для любого достаточно малого 
рассмотрим отрезок 
, где 
— точка кривой , отстоящая от 
на малое расстояние 
, а 
— точка пересечения стороны и прямой, проходящей через точку с углом наклона 
(см. рис. 1).
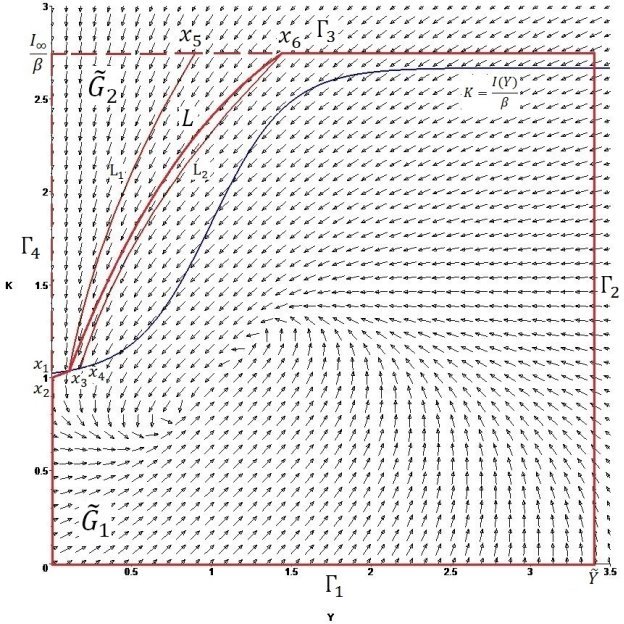
Рис. 1. Иллюстрация к доказательству теоремы 1. Векторное поле системы (1). Множество 
Поскольку функция 
— возрастающая вблизи 0, то при всех достаточно малых отрезок лежит ниже кривой . А так как 
, то при всех сколь угодно малых в каждой точке этого отрезка векторное поле системы (1) направленно внутрь множества . При этом для всех достаточно малых значений отрезок 
отстоит от кривой не более чем на величину 
.
Наряду с точкой 
рассмотрим лежащую справа от неё на расстоянии точку 
на кривой 
. Пусть 
и 
— кривые, образованные траекториями системы (6) приходящими в точки и из множества . В силу вида системы (6) такие траектории существуют и при всех достаточно малых и они не имеют общих точек с кривой , кроме и . Пусть 
и 
— точки пересечения кривых и со стороной прямоугольника . Поскольку обе кривые и являются графиками траекторий системы (6), то несложно показать, что существует такая кривая 
, соединяющая точки и , что она трансверсальна векторному полю системы (6), т. е. векторное поле системы (1) на кривой 
направленно внутрь множества .
Пусть 
, 
, 
и 
— стороны прямоугольника 
, лежащего внутри прямоугольника и отстоящего от него на малую величину 
. Рассмотрим замкнутую непрерывную кривую 
состоящую из сторон , 
прямоугольника , части его стороны , лежащей правее ее пересечения с 
, части кривой до точки , части отрезка , до пересечения с и оставшейся части стороны . Выбирая при фиксированном произвольно малом сначала достаточно малое , а затем достаточно малое получаем непрерывную замкнутую кривую лежащую внутри прямоугольника , и отстоящую от его границы не более чем на величину . По построению эта кривая не имеет точек самопересечения и при всех достаточно малых в каждой точке векторное поле системы (1) направлено во внутрь множества . □
Следствие. Из доказанной теоремы вытекает, что в случае, когда система (1), взятая с функциями инвестиций и сбережений (2), имеет в области единственное неустойчивое положение равновесия, в силу теоремы Пуанкаре-Бендиксона [2], она имеет в области замкнутую периодическую траекторию.
Численное моделирование
Аналогично [4], выберем в качестве функции — логистическую функцию:
(7)
Здесь параметры
и 
— положительные числа. При заданных положительных значениях 
и 
соответствующие функции инвестиций и сбережений определяются условиями (2). Очевидно, функция удовлетворяет всем сделанным ранее предположениям.
Следуя [4] выберем следующие значения параметров:
(8)
В этом случае результаты численного моделирования в среде MAPLE показывают, что система (1) имеет периодическую траекторию (см. рис. 2).
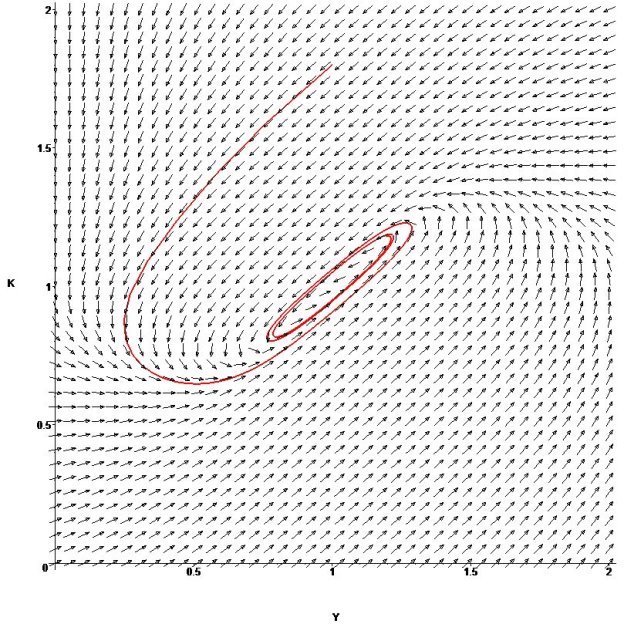
Рис. 2. Численное моделирование. Периодическая траектория
Действительно, в области система (1) имеет единственное положение равновесия 
. Матрица линеаризованной в окрестности положения равновесия 
имеет вид
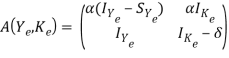(9)
Подставляя заданные функции инвестиций и сбережений (см. (2), (7)) и значения параметров (8) получаем, что в этом случае матрица (9) имеет два комплексно-сопряженных собственных значения, имеющих положительные действительные части:
, 
.
Таким образом, положение равновесия — неустойчивый фокус (см. [5]).
Поскольку
— единственное неустойчивое положение равновесия, то в данном случае, в силу теоремы 1 система (1) имеет периодическую траекторию.
Заключение
В статье рассматривается модифицированная модель бизнес-цикла Н. Калдора. Данная модель включает нелинейную систему дифференциальных уравнений, описывающих динамику капитали и национального дохода в рыночной экономике. Приводится строгое обоснование применения теоремы Пуанкаре-Бендиксона о существовании замкнутых периодических траекторий. При помощи численного моделирования продемонстрирована соответствующая траектория.
Литература:
1. N. Kaldor, A model of trade cycle, The Economic Journal, 1940, vol. 50, No. 197, pp. 78–92.
2. Ф. Хартман, Обыкновенные дифференциальный уравнения, М.: Мир, 1970.
3. H. -W. Lorenz, Nonlinear Dynamical Economics and Chaotic Motion, Berlin, 1993.
4. Т. В. Рязанова, Стохастические аттракторы и индуцированные шумом явления в моделях экономической динамики. Отчет о научно- исследовательской работе, УрФУ, Екатеринбург, 2013.
5. Л. С. Понтрягин, Обыкновенные дифференциальный уравнения, М.: Наука, 1974.
