Данная работа является продолжением статьи [1]. Проекции векторов ![]() и
и ![]() выведены на основе интегрирующих звеньев с моделированием в Simulink.
выведены на основе интегрирующих звеньев с моделированием в Simulink.
В работе [1] были получены уравнения (7) и (8) для расчета isx в Script-Simulink:
![]()
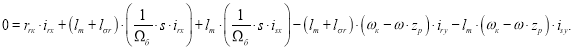
Исключим слагаемые с ![]() . Для этого умножим первое уравнение на (lm+lσr), а второе – на lm:
. Для этого умножим первое уравнение на (lm+lσr), а второе – на lm:
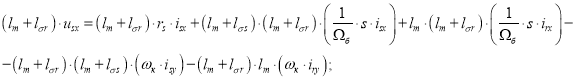
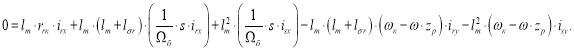
Наконец, вычтем второе уравнение из первого:
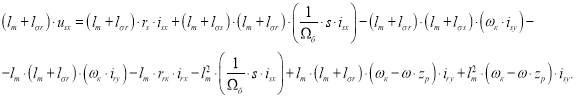
Перенесем слагаемые с ![]() в левую часть:
в левую часть:
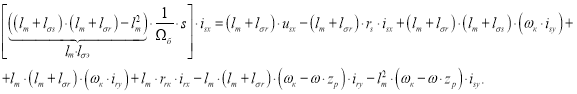
Разделим обе части уравнения на ![]() :
:
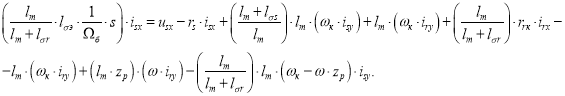
Обозначим:
![]()
![]()
Получим:
![]()
Ток ![]() определится в следующем виде:
определится в следующем виде:
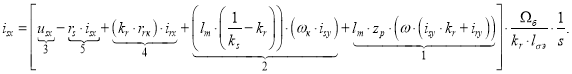
Структурная схема тока ![]() по оси +1 в Script-Simulink приведена на рис. 1.
по оси +1 в Script-Simulink приведена на рис. 1.
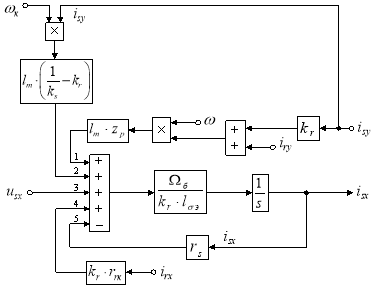
Рис. 1. Структурная схема для определения тока isx в Script-Simulink
Трансформируем структурную схему на рис. 1 в оболочку, позволяющую производить расчет коэффициентов в отдельном блоке Subsystem. Для этого вместо операторов с коэффициентами, рассчитываемыми в Script, установим блоки перемножения, к которым подведены сигналы с результатами расчетов в Simulink, как показано на рис. 2.
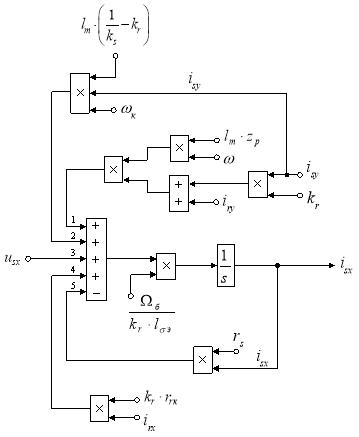
Рис. 2. Структурная схема для определения тока isx в Simulink
Произведем аналогичную трансформацию при определении тока ![]() по оси +1. Повторим уравнения (7) и (8):
по оси +1. Повторим уравнения (7) и (8):
![]()
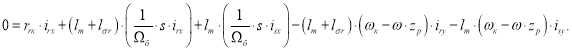
Исключим слагаемые с ![]() . Для этого умножим первое уравнение на
. Для этого умножим первое уравнение на ![]() , а второе – на
, а второе – на ![]() :
:
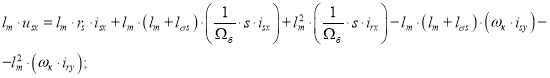
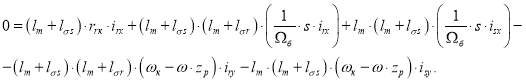
Вычитаем второе уравнение из первого:
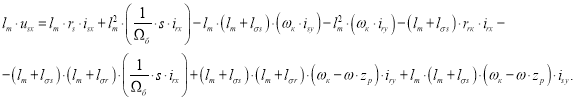
Перенесем слагаемые с 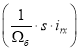 в левую часть:
в левую часть:
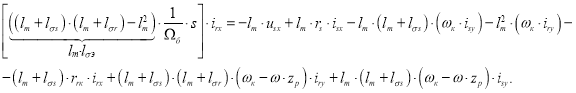
Разделим обе части уравнения на ![]() :
:
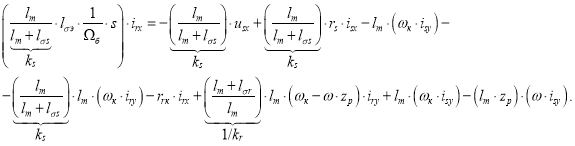
Получим:
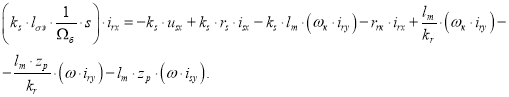
Определим ток ![]() :
:
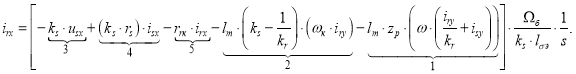
Структурная схема тока ![]() по оси +1 в Script-Simulink приведена на рис. 3.
по оси +1 в Script-Simulink приведена на рис. 3.
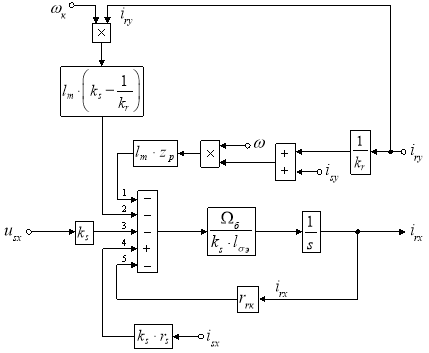
Рис. 3. Структурная схема для определения тока irx в Script-Simulink
Расчет коэффициентов будем производить в отдельном блоке Subsystem, поэтому вносим в структурную схему на рис. 3 блоки перемножения (рис. 4).
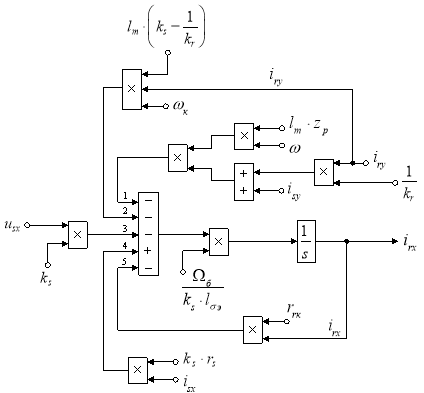
Рис. 4. Структурная схема для определения тока irx в Simulink
Для расчета тока ![]() приведем уравнения (9) и (10) из работы [1]:
приведем уравнения (9) и (10) из работы [1]:
![]()
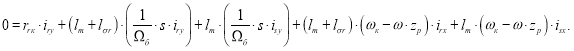
Исключим слагаемые с ![]() . Для этого первое уравнение умножим на
. Для этого первое уравнение умножим на ![]() , а второе – на
, а второе – на ![]() . Далее, второе уравнение вычтем из первого:
. Далее, второе уравнение вычтем из первого:
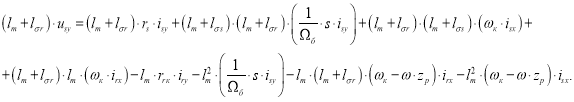
Перенесем слагаемые с ![]() в левую часть:
в левую часть:
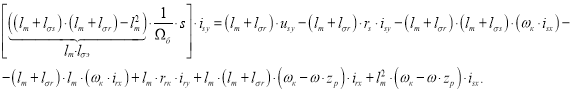
Разделим обе части уравнения на
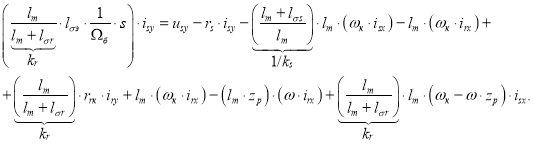
Получим:
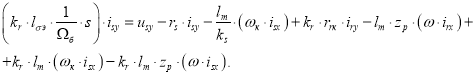
Определим ток ![]() :
:
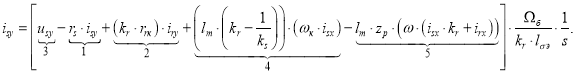
Структурная схема тока ![]() по оси +j в Script-Simulink приведена на рис. 5.
по оси +j в Script-Simulink приведена на рис. 5.
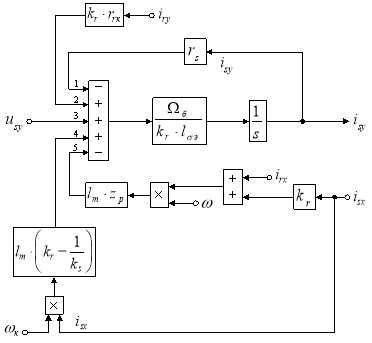
Рис. 5. Структурная схема для определения тока isy в Script-Simulink
Подготовим эту схему для расчета в Simulink (рис. 6).
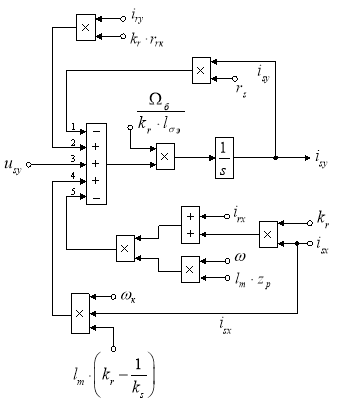
Рис. 6. Структурная схема для определения тока isy в Simulink
Для расчета тока ![]() повторим уравнения (9) и (10):
повторим уравнения (9) и (10):
![]()
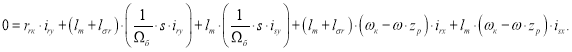
Исключим слагаемые с ![]() . Для этого умножим первое уравнение на
. Для этого умножим первое уравнение на ![]() , а второе – на
, а второе – на ![]() . Далее, вычтем второе уравнение из первого:
. Далее, вычтем второе уравнение из первого:
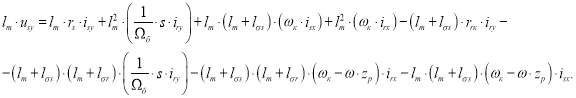
Перенесем слагаемые с ![]() в левую часть:
в левую часть:
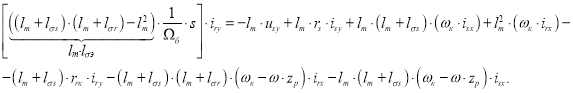
Разделим обе части уравнения на ![]() :
:
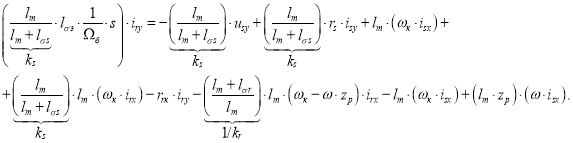
Получим:
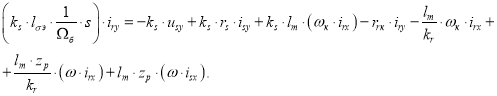
Определим ток ![]() :
:
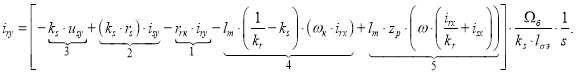
Структурная схема тока iry по оси +j в Script-Simulink приведена на рис. 7.
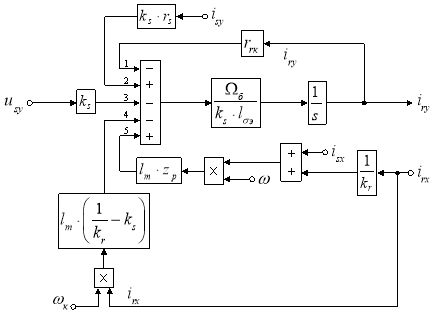
Рис. 7. Структурная схема для определения тока iry в Script-Simulink
Схема для расчета iry в Simulink представлена на рис. 8.
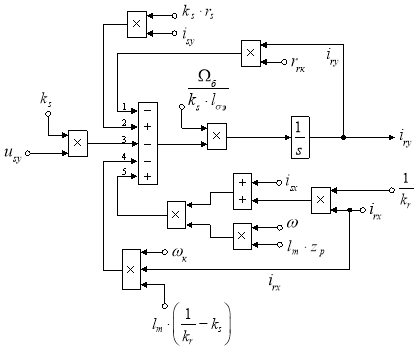
Рис. 8. Структурная схема для определения тока iry в Simulink
На рис. 9 представлена структурная схема для реализации уравнения электромагнитного момента в Simulink:
![]()
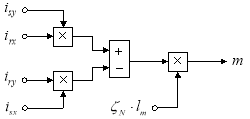
Рис. 9. Математическая модель определения электромагнитного момента m в Simulink
Из уравнения движения выразим механическую угловую скорость вращения вала двигателя (рис. 10):
![]()
![]()
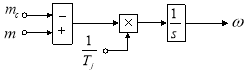
Рис. 10. Математическая модель уравнения движения
Математическая модель асинхронного двигателя с короткозамкнутым ротором с переменными is – ir на выходе интегрирующих звеньев в Simulink приведена на рис. 11, …, 15.
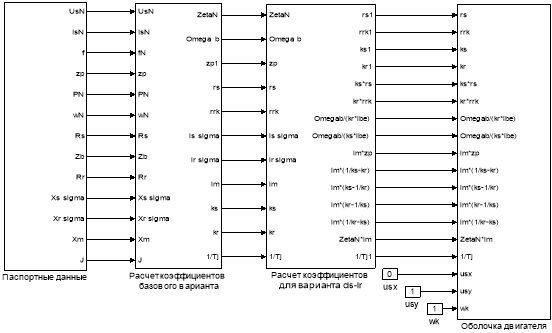
Рис. 11. Общая схема математической модели асинхронного двигателя с переменными is – ir на выходе интегрирующих звеньев в Simulink
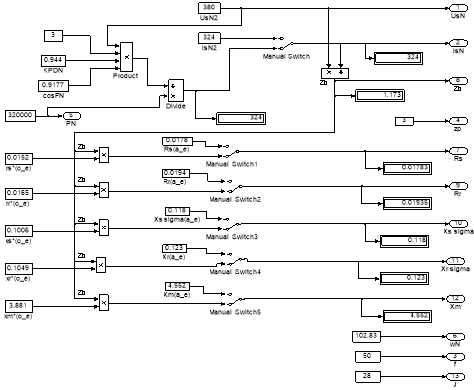
Рис. 12. Паспортные данные
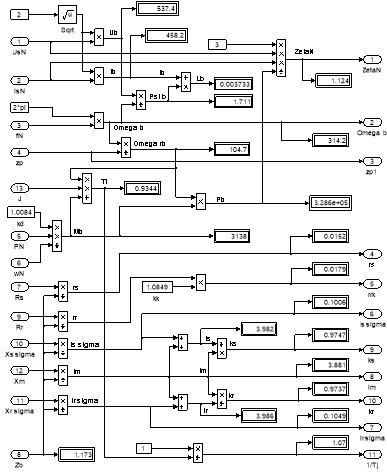
Рис. 13. Расчет коэффициентов базового варианта
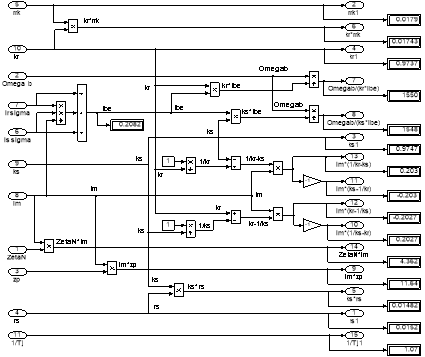
Рис. 14. Расчет коэффициентов для варианта с переменными is – ir
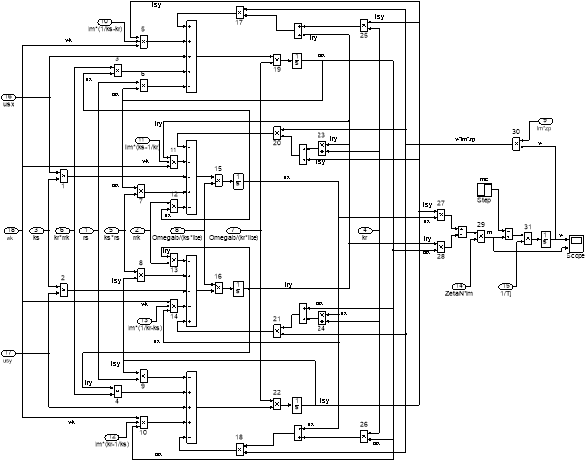
Рис. 15. Оболочка модели асинхронного двигателя с переменными is – ir на выходе интегрирующих звеньев в Simulink
Эту же схему можно представить в более компактной форме с использованием блоков Goto и From (рис. 16) и отдельных субблоков с расчетами токов, приведенных на рис. 17 и 18.
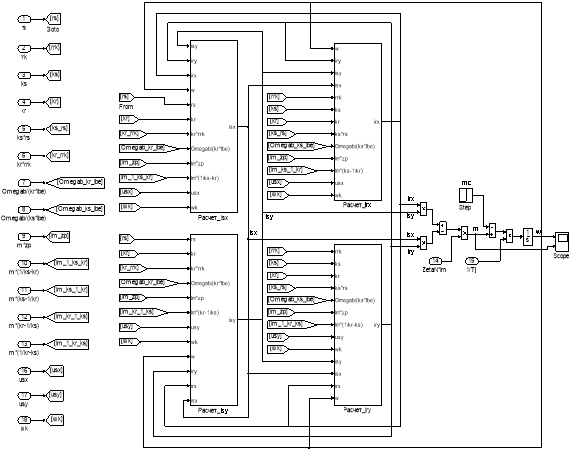
Рис. 16. Оболочка модели асинхронного двигателя с применением блоков Goto и From
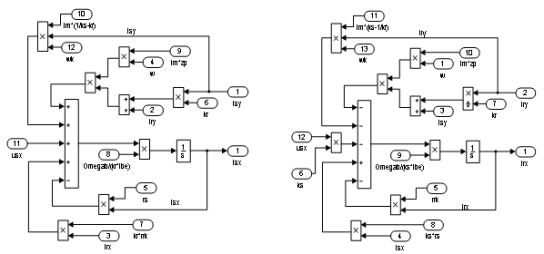
Рис. 17. Схемы для расчета токов isx и irx
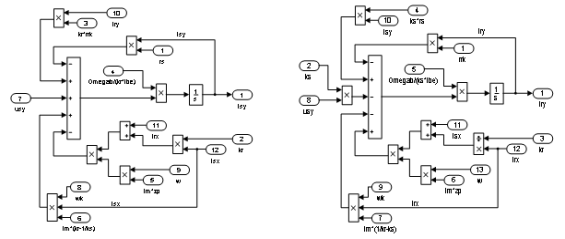
Рис. 18. Схемы для расчета токов isy и iry
В работах [2] и [3] дан образец расчета параметров асинхронного двигателя.
Номинальные данные:
Номинальный режим работыS1;
Номинальная мощность![]()
Номинальное фазное напряжение![]()
Номинальный фазный ток![]()
Номинальная частота![]()
Номинальная синхронная скорость![]()
Номинальная скорость ротора
Номинальный КПД![]()
Номинальный коэффициент мощности![]()
Число пар полюсов![]()
Параметры Т-образной схемы замещения при номинальной частоте:
Активное сопротивление обмотки статора![]()
Индуктивное сопротивление рассеяния обмотки статора![]()
Активное сопротивление обмотки ротора, приведенное к статору![]()
Индуктивное сопротивление рассеяния обмотки ротора, приведенное статору![]()
Главное индуктивное сопротивление![]()
Суммарный момент инерции двигателя и механизма![]()
Базисные величины системы относительных единиц:
Напряжение![]()
Ток![]()
Частота![]()
Скорость ротора![]()
Сопротивление![]()
Потокосцепление![]()
Индуктивность![]()
Используя номинальные данные двигателя, определяем:
![]()
где![]() – коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (k∆ = 1,0084).
– коэффициент, учитывающий различие значений электромагнитного момента и момента на валу двигателя в номинальном режиме (k∆ = 1,0084).
В качестве базисной мощности выбираем значение электромагнитной мощности двигателя в номинальном режиме, определяемое по следующей формуле:
![]()
Относительные значения параметров схемы замещения двигателя:
![]()
![]()
![]()
![]()
![]()
Механическая постоянная времени:
![]()
Номинальное значение скольжения:
![]()
Относительное значение номинальной скорости ротора:
![]()
Нормирующий энергетический коэффициент:
![]()
![]()
![]()
![]()
![]()
При расчете режимов работы, для того чтобы ![]()
![]()
![]()
![]() и
и ![]() , необходимо откорректировать
, необходимо откорректировать ![]()
где![]() – корректирующий коэффициент [3, с. 296].
– корректирующий коэффициент [3, с. 296].
![]() - коэффициент, показывающий отношение
- коэффициент, показывающий отношение ![]() к
к ![]() .
.
Расчет коэффициентов для математической модели с переменными ![]() :
:
![]()
![]()
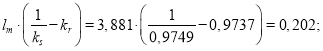
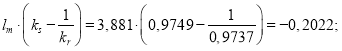

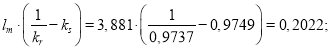
![]()
![]()
![]()
Результаты моделирования асинхронного двигателя представлены на рис. 19.
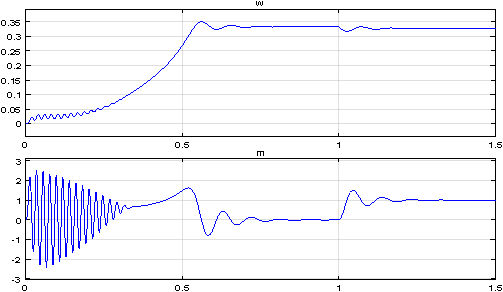
Рис. 19. Графики скорости и момента
Литература:
- Емельянов А. А., Бесклеткин В. В., Пестеров Д. И., Юнусов Т. Ш., Воротилкин Е. А., Камолов И. И., Карпенко К. Д., Попов С. Ю., Зашихин Е. В., Серебров А. А., Власова А. А. Математическая модель асинхронного двигателя с переменными is – ir на выходе апериодических звеньев в Simulink-Script // Молодой ученый. – 2016. – №30. – C. 14-28.
- Шрейнер Р. Т. Математическое моделирование электроприводов переменного тока с полупроводниковыми преобразователями частоты. – Екатеринбург: УРО РАН, 2000. – 654 с.
- Шрейнер Р. Т. Электромеханические и тепловые режимы асинхронных двигателей в системах частотного управления: учеб. пособие / Р. Т. Шрейнер, А. В. Костылев, В. К. Кривовяз, С. И. Шилин. Под ред. проф. д. т. н. Р. Т. Шрейнера. – Екатеринбург: ГОУ ВПО «Рос. гос. проф.-пед. ун-т», 2008. – 361 с.







