В данной статье разработана система коррекции ошибок при вводе данных на основе сети Хемминга, а также рассматривается приложение на языке Java, реализующее данную систему.
Ключевые слова: нейронные сети, сеть Хемминга, нечёткий поиск, коррекция ошибок
Постановка задачи.
Под нечётким поиском подразумевается нахождение того же образца, который подаётся на вход, или близкого к нему значения. Обычно для решения таких задач применяются различные метрики (Левенштейна, Дамерау-Левенштейна, метод N-грамм, BK-деревья и т. д.). В данной статье будет предложен алгоритм поиска на основе нейронной сети Хемминга.
Сеть Хемминга. Принцип работы.
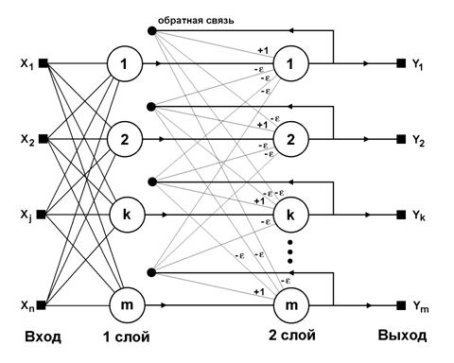
Рис. 1. Структурная схема сети Хемминга
Нейронная сеть Хемминга состоит из двух слоёв, количество нейронов в которых равно количеству образцов (классов), хранимых в словаре [1]. Алгоритм работы базируется на нахождении расстояния Хемминга между поданным на вход вектором и эталонными образами. Сеть должна предпочесть образец, который имеет наименьшее расстояние Хемминга до входного вектора.
Описание моделируемой системы.
Каждое слово может быть описано входным вектором X = {
public class Neuron {
private double[] weights;
private double y;
private double s;
}
Листинг 1. Структура нейрона
public class HammingNetwork {
private int n;
private int m;
private Neuron[] firstLayer;
private Neuron[] secondLayer;
}
Листинг 2. Структура сети
Стадия инициализации.
Заполнение весовых коэффициентов нейронов первого слоя:
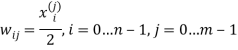 , где
, где ![]() — i-ая координата j-го образца.
— i-ая координата j-го образца.
Расчёт состояний нейронов первого слоя.
На вход подаётся вектор X, начинается подсчёт состояний нейронов первого слоя и их аксонов: 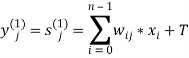 , где
, где ![]() .
.
private void fillFirstLayer(int[] x) {
x = transformVector(x);
double t = (double) n / 2;
for (int j = 0; j < m; j++) {
Neuron currentNeuron = firstLayer[j];
double state = 0;
for (int i = 0; i < n; i++) {
state += (currentNeuron.getWeight(i) * x[i]);
}
state += t;
currentNeuron.setS(state);
currentNeuron.setY(state);
}
}
Листинг 3. Заполнение первого слоя нейронов
Расчёт состояний нейронов второго слоя
Производится подсчёт состояний нейронов второго слоя: 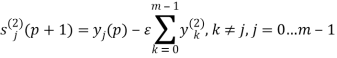 и их аксонов:
и их аксонов: ![]() , где p — номер итерации, а f — активационная функция. Активационная функция имеет следующий вид:
, где p — номер итерации, а f — активационная функция. Активационная функция имеет следующий вид: 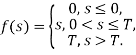 . Синапсы обратных связей нейронов второго слоя принимают значения
. Синапсы обратных связей нейронов второго слоя принимают значения ![]() , где
, где ![]() . Для простоты можно принять
. Для простоты можно принять ![]() . Подсчёт состояний и аксонов нейронов второго слоя продолжается до тех пор, пока выходы нейронов не стабилизируются. Для этого вводится величина eMax, которая определяет максимальное отклонение для координат выходного вектора [2].
. Подсчёт состояний и аксонов нейронов второго слоя продолжается до тех пор, пока выходы нейронов не стабилизируются. Для этого вводится величина eMax, которая определяет максимальное отклонение для координат выходного вектора [2].
private double[] calculateSecondLayer() {
final double epsilon = (double) 1 / m;
final double eMax = 0.1;
final double t = (double) n / 2;
List
for (int j = 0; j < m; j++) {
Neuron currentNeuron = secondLayer[j];
currentNeuron.setS(firstLayer[j].getS());
currentNeuron.setY(firstLayer[j].getY());
lastY.add(firstLayer[j].getY());
}
List
boolean outputChange = false;
do {
List
for (int j = 0; j < m; j++) {
Neuron currentNeuron = secondLayer[j];
double sum = calculateSum(lastY, epsilon, j);
currentNeuron.setS(currentNeuron.getY() - sum);
double output = currentNeuron.getY();
double newOutput = activateFunction(t, currentNeuron.getS());
outputChange = Math.abs(output - newOutput) > eMax;
currentNeuron.setY(newOutput);
currentY.add(newOutput);
}
lastY = currentY;
outputs = new ArrayList<>();
outputs.addAll(currentY);
} while (outputChange);
return outputs.stream().mapToDouble(i -> i).toArray();
}
private double calculateSum(List
double sum = 0;
for (int k = 0; k < m; k++) {
if (k != j) {
sum += y.get(k);
}
}
sum *= epsilon;
return sum;
}
Листинг 4. Заполнение второго слоя нейронов
Производительность
Были произведены замеры времени, потраченного построенной моделью на обработку входного вектора и выдачу результата. Стоит заметить, что количество потраченного времени зависит не только от количества слов в словаре, но и от выбора величины eMax, которая влияет на количество итераций при расчёте состояний нейронов второго слоя.
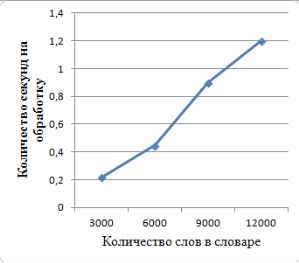
Рис. 2. График зависимости времени обработки от размеров словаря
Заключение
С помощью сети Хемминга можно организовать систему автоматической коррекции ошибок. Время обработки информации с увеличением объёма словаря растёт почти линейно. Однако нужно отметить некоторые ограничения. Если при вводе информации были допущены опечатки, то алгоритм работает корректно, но при пропуске или добавлении лишнего символа будут возникать ошибки. Также стоит отметить, что из-за одинакового количества входов для образцов, построенная сеть может различать только слова одинаковой длины. Поэтому для обработки слов разной длины необходимо использовать комплекс таких сетей.
Литература:
- Короткий С. Нейронные сети Хопфилда и Хэмминга.
- Нейронные сети Хемминга [Электронный ресурс], http://neuronus.com/nn/38-theory/971-nejronnye-seti-khemminga.html (дата обращения: 04.01.2017).







