Принято считать [1], что при вращении барабана в период центробежного отжима изделия распределяются по обечайке в виде неравномерного кольца (рис.1).
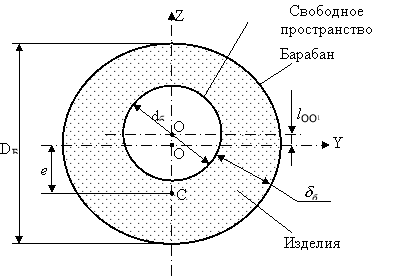
Рис. 1. Схема распределения изделий по обечайке барабана при отжиме: DБ — диаметр барабана, dб — диаметр окружности с центром О1 сечения свободного пространства, образованного текстильными изделиями (бельем) при отжиме (внутренний диаметр кольца изделий); е — эксцентриситет центра масс кольца изделий; lОО1 — расстояние между осью вращения барабана с центром окружности О и центром окружности О1 сечения свободного пространства, образованного изделиями; б — толщина слоя изделий, распределенных по обечайке барабана в виде неравномерного кольца при отжиме
При этом неравномерность распределения изделий, вызванная случайным характером протекающих процессов, определяется смещением центра О1 окружности свободного пространства на расстояние lОО1 и появившегося в результате этого эксцентриситета rе — расстояния ОС от оси вращения барабана до центра масс изделий С.
Здесь ордината zС центра масс изделий С находится по известной формуле [2], имеющей вид:
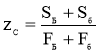 ,(1)
,(1)
где SБ и Sб — статические моменты кругового поперечного сечения барабана с центром О и кругового поперечного сечения свободного пространства с центром О1 соответственно; FБ и Fб — площади кругового поперечного сечения барабана с центром О и кругового поперечного сечения свободного пространства с центром О1 соответственно.
Очевидно, что в соответствии с рисунком 1 площади FБ и Fб равны:
![]() ;(2)
;(2)
![]() .(3)
.(3)
Определим статические моменты:
![]() ,(4)
,(4)
где zБ=0 — координата центра масс круглого сечения с центром О, образованного обечайкой барабана; откуда SБ=0;
![]() ,(5)
,(5)
где zб = lОО1 — координата центра масс круглого сечения с центром О1, образованного свободным пространством изделий; откуда
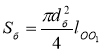 .(6)
.(6)
С учетом полученных выражений (2) — (6), а также с учетом того, что площадь Fб и статический момент Sб, относящиеся к окружности поперечного сечения свободного пространства с центром О1, будут входить в формулу (1) со знаком «минус» (так как свободное пространство не содержит изделий), выражение (1) примет следующий вид:
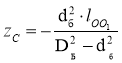 .(7)
.(7)
Так как расстояние ОС=rе, где положение центра масс С определяется ординатой zС, то эксцентриситет rе по абсолютной величине будет равен:
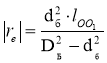 .(8)
.(8)
Величина lОО1 определяется в зависимости от соотношения DБ и dб. Существуют два варианта соотношения DБ и dб: 1) dб0,5DБ, 2) dб>0,5DБ. На рисунке 2 показаны крайние случаи расположения кольцевого слоя изделий в барабане: на рисунке 2,а для 1-го варианта при dб0,5DБ, на рисунке 2,б для 2-го варианта при dб>0,5DБ.
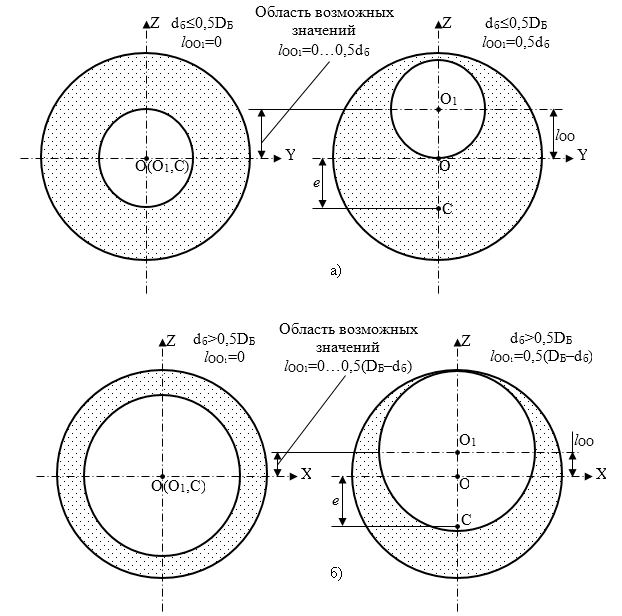
Рис. 2. Расположение кольца изделий в барабане в зависимости от вариантов соотношения DБ и dб
Для 1-го варианта при dб0,5DБ значение lОО1 будет изменяться случайно в промежутке от lОО1=0 до lОО1=0,5dб (рис.2.2, а). Для 2-го варианта при dб>0,5DБ значение lОО1 будет изменяться случайно в промежутке от lОО1=0 до lОО1=0,5(DБ–dб) (рис.2.2, б). Таким образом, величина lОО1 имеет ограничение: lОО10,5dб при dб0,5DБ и lОО10,5(DБ–dб) при dб>0,5DБ. Очевидно, что значение dб определяется массой загруженных в барабан текстильных изделий (белья) mбо и размерами барабана (диаметром DБ и длиной LБ).
При установлении максимального значения диаметра окружности сечения свободного пространства dбmax, соответствующему минимальной величине загрузки изделий mбоmin, будем считать, что толщина изделий Б, распределенных в виде кольца по обечайке барабана при отжиме, составляет не менее Б0,01 м. Тогда dбmax=(DБ–2Б)=(DБ–0,02) м. Таким образом, значения диаметра dб находятся в промежутке от dбmin=0 до dбmax=(DБ–0,02) м.
Отметим, что предложенный выше подход по определению эксцентриситета rе центра масс отжимаемых изделий предполагает следующее допущение распределение плотности изделий по всему объему барабана принимается равномерным. Данное допущение основано, с одной стороны, на том, что практически невозможно учесть случайное реальное распределение плотности изделий по объему барабана. С другой стороны, как показали расчеты, при максимальной разности между плотностью изделий в различных частях барабана, величина эксцентриситета может изменяться от расчетного значения не более чем на 4 %.
Используя полученные выше соотношения и формулу (8), определим значения эксцентриситета rе центра масс изделий при различных значениях dб и lОО1 для диапазона величин диаметра барабана DБ=(0,4…0,5) м. Графики зависимостей эксцентриситета rе от dб и lОО1 при DБ=0,4 м и DБ=0,5 м приведены на рисунках 3–4.
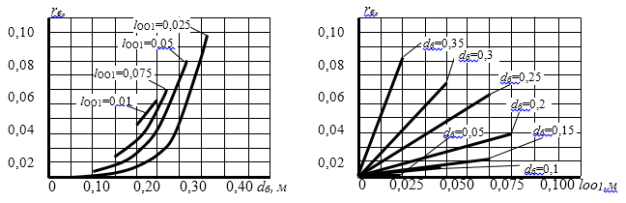
Рис. 3. Графики зависимостей эксцентриситета rе от dб и lОО1 при DБ=0,40 м
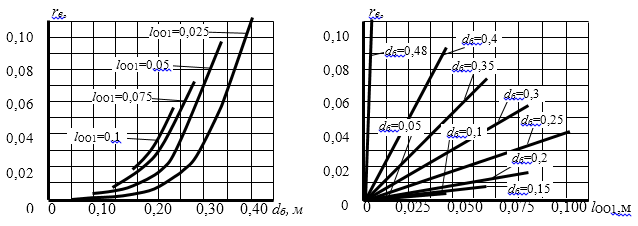
Рис.4. Графики зависимостей эксцентриситета rе от dб и lОО1 при DБ=0,50 м
Ниже на рисунке 5 показано семейство графиков зависимости rе=f(DБ) при различных значениях диаметра dб (здесь значения rе взяты как средние значения из полученного диапазона rе при различных lОО1).
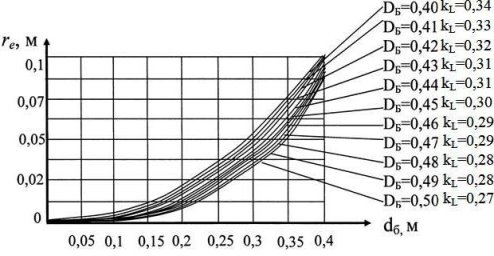
Рис. 5. Графики функции rе=f(dб) при различных DБ
Анализ полученных данных показывает, что при увеличении внутреннего диаметра dб кольца изделий (что соответствует снижению коэффициента загрузки kз или увеличению степени деформации изделий при отжиме) величина эксцентриситета rе нелинейно увеличивается. При снижении же диаметра барабана DБ и коэффициента kL значения эксцентриситета rе растут.
Таким образом, выше было показано, что основными факторами, определяющими границы диапазона возможных случайных значений эксцентриситета центра масс изделий при отжиме являются соотношение геометрических параметров стирального барабана, режим его вращения и масса отжимаемых изделий.
Литература:
- Лебедев, В. С. Технологические процессы машин и аппаратов в производствах бытового обслуживания / В. С. Лебедев. — М.: Легпромбытиздат, 1991. — 336 с.
- Яблонский, А. А. Курс теоретической механики. Статика, кинематика, динамика / А. А. Яблонский, В. М. Никифорова. — М.: КноРус, 2010. — 608 с.







