При выборе метода функционирования устройства классификации сигналов необходимо учитывать характерные особенности источников сигналов (частота излучения, длительность импульсов, пространственное расположение источников и т. д.), требования по достоверности результатов классификации, на максимальное допустимое время классификации и на структуру аппаратных и программных средств устройства.
Ключевые слова: вектор, сигнал, квантование
В данной статье рассматривается метод классификации сигналов, суть которого заключается в разбиении всех классов на группы и подгруппы на основе набора вторичных признаков, в которых по возможности, сконцентрирована информация о наиболее существенных свойствах сигналов.
Сигнал ![]() , поступивший на классификацию, представлен виде вектора вторичных признаков
, поступивший на классификацию, представлен виде вектора вторичных признаков![]() и характеризуется тремя признаками
и характеризуется тремя признаками ![]() . Где
. Где ![]() — качественный признак, указывающий на номер максимальной компоненты вектора
— качественный признак, указывающий на номер максимальной компоненты вектора ![]() ;
; ![]() — количественный признак, характеризующий разброс компонентов вектора
— количественный признак, характеризующий разброс компонентов вектора ![]() ;
;![]() — двухкомпонентный признак, описывающий уровень квантования (α) и код огибающей сигнала (
— двухкомпонентный признак, описывающий уровень квантования (α) и код огибающей сигнала (![]() ), полученный на данном уровне.
), полученный на данном уровне.
Результат классификации зависит от точности формирования кода огибающей сигнала — признака ![]() . Признак
. Признак ![]() представляет собой кортеж сочетаний «I« и «О« и отражает наиболее существенные изменения (перепады) огибающей классифицируемого сигнала, а также не зависит от масштабов представления его параметров. Кортеж получается в результате сравнения каждого из компонентов вектора
представляет собой кортеж сочетаний «I« и «О« и отражает наиболее существенные изменения (перепады) огибающей классифицируемого сигнала, а также не зависит от масштабов представления его параметров. Кортеж получается в результате сравнения каждого из компонентов вектора ![]() с некоторым пороговым уровнем
с некоторым пороговым уровнем ![]() по условию
по условию ![]() . При удовлетворении данного условия i –ой компоненте кортежа
. При удовлетворении данного условия i –ой компоненте кортежа ![]() присваивается «I«, в противном случае — «О«. В данном случае точность представления вида огибающей сигнала кортежем
присваивается «I«, в противном случае — «О«. В данном случае точность представления вида огибающей сигнала кортежем ![]() существенно зависит от численного значения
существенно зависит от численного значения ![]() .
.
Для сигналов, имеющих равномерное изменение огибающей, значение ![]() определяется простыми выражениями:
определяется простыми выражениями:
‒ для дискретных сигналов 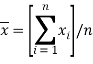 или
или ![]() /2;
/2;
‒ для непрерывных сигналов ![]() .
.
В случае, когда классифицируемый сигнал имеет неравномерное изменение огибающей, значение ![]() может быть определено как
может быть определено как
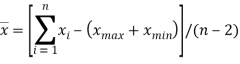 .
.
где
Дли точного описания огибающей сигнала производится его квантование по уровню и на каждом уровне определяется код вида огибающей сигнала. В этом случае численное значение порога ![]() , находящегося в интервале
, находящегося в интервале ![]() , определяется из выражения
, определяется из выражения
![]()
где α порядковый номер шага квантования, на котором формируется код огибающей сигнала.
![]()
а ![]() шаг квантования, который изменяется пропорционально к масштабам представления параметров сигнала
шаг квантования, который изменяется пропорционально к масштабам представления параметров сигнала ![]() , значение которого вычисляется по формуле
, значение которого вычисляется по формуле
![]()
При формировании признака ![]() в данном разделе рассматриваются следующие случаи:
в данном разделе рассматриваются следующие случаи:
-
Признак
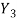 является вектором
является вектором 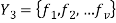 , компоненты которого соответствуют кодам полученным на каждом шаге квантовании. При этом не все компоненты признака
, компоненты которого соответствуют кодам полученным на каждом шаге квантовании. При этом не все компоненты признака 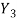 отражают информацию об изменениях огибающей сигнала. В данном случав признак
отражают информацию об изменениях огибающей сигнала. В данном случав признак 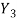 наиболее полно представляет классифицируемый сигнал, но требуются значительные вычислительные затраты при его сравнении с соответствующими эталонными признаками.
наиболее полно представляет классифицируемый сигнал, но требуются значительные вычислительные затраты при его сравнении с соответствующими эталонными признаками.
- Для уменьшения вычислительных затрат в качестве компонентов
признака ![]() можно использовать коды, полученные на четных (нечетных) значениях α. В частном случае компонентами признака
можно использовать коды, полученные на четных (нечетных) значениях α. В частном случае компонентами признака ![]() принимаются комбинации кодов огибающей сигнала, полученные при:
принимаются комбинации кодов огибающей сигнала, полученные при:
![]()
3. Более оптимальным является случай, когда ![]() представляется в виде двухкомпонентного признака
представляется в виде двухкомпонентного признака ![]() где α, соответствует номеру шага квантования, на котором код
где α, соответствует номеру шага квантования, на котором код ![]() содержит наибольшее количество переходов типа «IO», «OI» и сравнительно точно отражает вид огибающей сигнала. При этом значение α остается постоянным для сигналов одного класса, представленных в различных масштабах измерения.
содержит наибольшее количество переходов типа «IO», «OI» и сравнительно точно отражает вид огибающей сигнала. При этом значение α остается постоянным для сигналов одного класса, представленных в различных масштабах измерения.
Приводимый метод классификации включает в себя четыре уровня, в первых трех уровнях которого, на основе сравнения соответствующих признаков сигнала и эталона, определяется подмножество классов, к которому принадлежит классифицируемый сигнал, а на последнем уровне находится конкретный класс на основе сравнения кодов огибающих сигнала и эталонов.
На первом и втором уровнях классификации осуществляется сравнение признаков ![]() и
и ![]() с соответствующими составляющими эталонного вектора по выражениям
с соответствующими составляющими эталонного вектора по выражениям ![]() , выполнение которых является необходимым условием отнесения классифицируемого сигнала g-му классу (g=I,К).
, выполнение которых является необходимым условием отнесения классифицируемого сигнала g-му классу (g=I,К).
На третьем и четвертом уровнях классификации осуществляется сравнение признаков ![]() эталонными признаками на основе выражений предикатов сходства неотрицательных чисел, которое для данного случая имеет вид
эталонными признаками на основе выражений предикатов сходства неотрицательных чисел, которое для данного случая имеет вид
![]() ,
,
и предиката сходства изображающих чисел
![]()
соответственно. Здесь ![]() и
и ![]() пороги сравнения признаков
пороги сравнения признаков ![]() и
и ![]() являются порогами схожести, а
являются порогами схожести, а ![]() — порогами сильного расхождения.
— порогами сильного расхождения.
Если предикаты ![]() то коэффициенту ω, определяющему номер подмножества классов, присваивается значение ω=2, а номер класса в подмножестве классов определяется согласно выражения g=g(3ω+3). В противном случае вычисляется соответствующий предикат сходства для порога сильного расхождения. При истинном значении предиката коэффициенту ω присваивается значение ω=1, а g=g(3ω+2), в противном случае ω=0 и g=g(3ω+1).
то коэффициенту ω, определяющему номер подмножества классов, присваивается значение ω=2, а номер класса в подмножестве классов определяется согласно выражения g=g(3ω+3). В противном случае вычисляется соответствующий предикат сходства для порога сильного расхождения. При истинном значении предиката коэффициенту ω присваивается значение ω=1, а g=g(3ω+2), в противном случае ω=0 и g=g(3ω+1).
Описанный метод, основанный на вычислении предикатов сходства вторичных признаков, позволяет ускорить процесс классификации за счет направленного выбора эталонных классов и существенно упростить данный процесс представлением сигналов в виде вектора вторичных признаков, компоненты которого являются инвариантными к масштабам представления параметров классифицируемого сигнала.
Выражения предикатов сходства в данном методе можно легко заменить на выражения метрик и мер близостей нелинейного пространства, что позволяет применять предлагаемый метод для классификации сигналов (объектов) при заданных границах классов.
Литература:
- Ходжиев К. К., Абдуллаев М. М. Об одном способе повышения быстродействия систем принятия решений.// Программное, алгоритмическое и техническое обеспечение АСУ ТП: Тез. докл. Всесоюзной НТК. — Ташкент. 1985, ч.4.
- Хасанов П. Ф., Ходжиев К. К. Нелинейное метрическое пространство для решения задач распознавания образов: Сб.науч.тр. Ташкент: ТяшПИ. I984, Вып.322.
- Поезжаева Е.В//Теория механизмов и механика систем машин. Учеб. Пособия/Е. В. Поезжаева.- Пермь: Изд-во Пермского национального исследовательского политехнического университета. 2014.-400







