В статье рассматривается электрическое поле, порождающее магнитное, которое оказывается переменным. Это переменное магнитное поле порождает электрическое. Таким образом, если возбудить с помощью колеблющихся зарядов переменное электромагнитное поле, то в окружающем заряды пространстве возникнет последовательность взаимных превращений электрического и магнитного полей, распространяющихся от точки к точке. Этот процесс будет периодическим во времени и в пространстве и следовательно, представляет собой волну.
Система уравнений для электромагнитного поля получена Максвеллом в середине XIX в. путем обобщения опытных данных электрическими зарядами, токами и магнитами. Уравнения Максвелла имеют очень глубокое физическое содержание, далеко выходящее за рамки тех фактов и представлений, на основе которых они были получены. Эти уравнения хорошо описывают быстропеременное электромагнитное поле, включая световые волны, и составляют основу теории излучения электромагнитных волн движущимися зарядами и теории взаимодействия света и вещества.
Уравнения Максвелла указывают, что электрическое и магнитное поле существуют одновременно и их совместное существование представляет собой электромагнитное поле.
Процесс распространения в пространстве электромагнитного поля называется электромагнитной волной. В отличие от механических волн, которые могут распространяться только в упругих средах, электромагнитные волны могут распространяться и в вакууме.
Для распространения электромагнитных волн не требуется присутствия дополнительных сред. В этом смысле электромагнитные волны в вакууме элементарны, то есть фундаментальны. Однако, и в вакууме область применимости уравнений Максвелла ограничена, причем более детальное рассмотрение показывает тесную связь теории электромагнитного поля с другими основными разделами физики, прежде всего с квантовой теорией. Вакуум может вести себя как своеобразная оптическая среда.
Электромагнитное поле имеет две компоненты — электрическую и магнитную. Первая описывается вектором электрической напряженности, вторая — вектором магнитной напряженности. В удобной для оптики гауссовой системе единиц уравнения Максвелла для электромагнитного поля в вакууме имеют вид
![]()
![]() (1.1)
(1.1)
![]()
![]() (1.2)
(1.2)
Здесь ![]() и
и ![]() — напряженности электрического и магнитного полей, c — скорость света в вакууме. Первое уравнение (1.1) представляет собой математическую формулировку закона электромагнитной индукции, а второе — показывает, что магнитное поле порождается переменным электрическим полем. Первое уравнение (1.2) выражает факт отсутствия статического электрического поля в вакууме, а второе — постулирует отсутствие магнитных зарядов.
— напряженности электрического и магнитного полей, c — скорость света в вакууме. Первое уравнение (1.1) представляет собой математическую формулировку закона электромагнитной индукции, а второе — показывает, что магнитное поле порождается переменным электрическим полем. Первое уравнение (1.2) выражает факт отсутствия статического электрического поля в вакууме, а второе — постулирует отсутствие магнитных зарядов.
Волновое уравнение. Уравнения (1.1)-(1.2) позволяют вывести замкнутые уравнения для полей![]() и
и![]() , которые называют волновым уравнением.
, которые называют волновым уравнением.
Дифференцируя второе уравнение (1.1) по времени и меняя порядок следования временной и пространственных производных, имеем
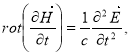 (1.3)
(1.3)
Воспользовавшись первым уравнением (1.1), получим
![]() (1.4)
(1.4)
Применяя известное из векторного анализа соотношение для дифференциальных операторов, преобразуем левую часть последнего уравнения к виду
![]() (1.5)
(1.5)
∆ — оператор Лапласа, который в декартовых координатах x, y, z имеет вид
![]() (1.6)
(1.6)
Поскольку в вакууме свободные заряды отсутствуют, т. е. div ![]() = 0, для вектора напряженности электрического поля получаем следующее уравнение
= 0, для вектора напряженности электрического поля получаем следующее уравнение
![]() (1.7)
(1.7)
Аналогичным образом получается уравнение для![]()
Уравнения (1.7) и (1.8) линейны по полю. Поэтому они эквивалентны совокупности скалярных уравнений того же самого вида, в каждое из которых входит только одна компонента напряженности электрического или магнитного поля. Действительно, запишем векторы ![]() и
и ![]() через декартовы компоненты
через декартовы компоненты ![]() и
и ![]() соответственно:
соответственно:
![]()
![]() (1.9)
(1.9)
![]() ,
, ![]() ,
, ![]() - единичные векторы («орты»), направленные вдоль осей x, y, z декартовой системы координат.
- единичные векторы («орты»), направленные вдоль осей x, y, z декартовой системы координат.
Умножая скалярно уравнения (1.7) и (1.8) последовательно на ![]() ,
, ![]() ,
, ![]() , получаем, что каждая из компонент полей
, получаем, что каждая из компонент полей ![]() или
или ![]() удовлетворяет скалярному уравнении
удовлетворяет скалярному уравнении
![]()
![]() (1.10)
(1.10)
Уравнения (1.7), (1.8) и (1.10) называются волновыми уравнениями. Они описывают распространения полей![]() и
и![]() в пространстве и времени. Их решения имеют характер распространяющихся волн.
в пространстве и времени. Их решения имеют характер распространяющихся волн.
Рассмотрим свойства световых волн на примере наиболее простых («эталлонных») волн. К числу таких волн относят плоские и сферические волны. Подчеркнем, что эти волны являются идеализациями и в природе их не существует, но они позволяют, как будет показано в дальнейшем, рассматривать процесс распространения любых световых волн.
Литература:
1. М. Б. Виноградова, О. В. Руденко, А. П. Сухоруков. Теория волн. М., Наука, 1991
2. Ю. А. Ананьев. Оптические резонаторы и лазерные пучки. М., Наука, 1990
3. М.Борн, Э.Вольф. Основы оптики. М., Наука, 1970
4. С. Г. Ахманов. Физическая оптика. Учебник — С.: МГУ, 2004, 213 с.







