Электрические нагрузки Рязанского государственного радиотехнического университета за май-август 2016 года



Рассмотрены электрические нагрузки Рязанского государственного радиотехнического университета за май-август 2016 года. Определены значения математического ожидания, дисперсии, среднего квадратического отклонения, коэффициента вариации электрических нагрузок, а также максимальное и минимальное значения нагрузок в сутки, месяц, квартал.

Ключевые слова: система электроснабжения, электрические нагрузки, максимальное и минимальное значения электрических нагрузок

Основой рациональной системы электроснабжения предприятий и бытовых потребителей являются режим их работы и предполагаемая величина электрических нагрузок.

Электрическая нагрузка высшего учебного заведения в течение суток неравномерна. Она преимущественно складывается из освещения помещений и работы лабораторных установок и бытовых приборов. Днем во время проведения занятий нагрузка возрастает, ночью снижается до минимума. Значительные изменения её наблюдаются в течение года, семестра, экзаменационной сессии, каникул и особенно при проведении специальных ремонтных работ.

Изменения и неравномерность нагрузки вызывают колебания уровня напряжения электрической энергии и снижают её качество, при этом увеличивается риск повреждения оборудования.

Актуальность работы заключается в исследовании нагрузок для расчета и прогнозирования возможных скачков нагрузки в сети и колебаний уровня напряжения и удержания их в допустимых значениях для потребления электрической энергии с наибольшей экономической выгодой.

Целью исследования является разработка возможных мероприятий по сбережению электроэнергии после изучения электрических нагрузок зданий и сооружений Рязанского государственного радиотехнического университета (РГРТУ).

Материал и методика исследования.

Анализировали показания электрических нагрузок РГРТУ за май-август месяцы 2016 года из акта фактического потребления электроэнергии по часам ООО «Рязанская городская муниципальная энергосбытовая компания». Исследуемый период (май-август), выбран из-за производимых ремонтных работ и, в связи с этим, роста нагрузки в электрической сети. Она значительно отличалась от нагрузки в период обучения (семестров) и зимних каникул.

В течение мая — августа месяцев 2016 года значения изменений нагрузки фиксировались каждый час ежедневно, в рабочие, выходные и праздничные дни. Получено 2952 значения изменения электрической нагрузки по РГРТУ. Все расчеты выполнялись в относительных величинах Р^*, каждое значение мощности Р_i за час соотносилось с максимальным значением мощности Р_max, зафиксированным в течение года

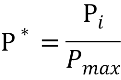.(1)

Электрическая нагрузка величина непрерывно изменяющаяся, так как потребители системы электроснабжения включаются или отключаются. Мощность, потребляемая электроприемниками, меняется с изменением загрузки рабочих машин. В зависимости от степени электрификации учебного процесса с течением времени изменяется общая электрическая нагрузка университета. Эти изменения, как правило, носят случайный характер, однако они подчиняются вероятностным законам, которые могут быть установлены с большой точностью при большом количестве опытных данных. Поэтому для анализа нагрузки использовали математический аппарат теории вероятностей.

Первоначально строили функцию и плотность распределения случайных значений нагрузки. При этом предполагалось, что результаты исследований подчиняются нормальному закону распределения.

Рассчитали значения математического ожидания, дисперсии и среднего квадратического отклонения случайной величины, [1].

Среднее значение случайной величины , определяли как среднее взвешенное значение (математическое ожидание), [2], то есть сумму произведений всех её значений и их вероятности:

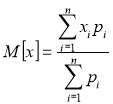(2)

Учитывая, что: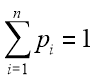

формула (2) соответствует:

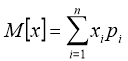(3)

Рассеивание случайной величины оценивали по значению дисперсии. Отклонение случайной величины от ее математического ожидания это есть математическое ожидание квадрата соответствующей центрированной величины, [2]:

X^о = x — M [x](4)

Значение дисперсии определяли как:

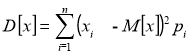(5)

или по формуле:

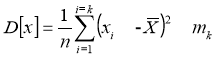,(6)

где: n — число опытов; k — число интервалов вариационного ряда; x_{i —} случайная величина; — среднее значение случайной величины; m_{k —} число отказов в интервале.

Квадратный корень из дисперсии (среднее квадратическое отклонение) определяли по выражению, [3]:

(7)

Среднее квадратическое отклонение характеризует разброс значений случайных величин относительно математического ожидания. Рассеивание значений случайных величин от математического ожидания приводит к большим значениям дисперсии и среднего квадратического отклонения.

Характеристику рассеивания случайной величины (коэффициент вариации) рассчитывали по формуле, [2]:

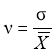(8)

где ϭ — среднее квадратическое отклонение; — среднее значение случайной величины.

Соответствие результатов исследования электрических нагрузок предполагаемому теоретическому закону распределения проверяли методом Пирсона (χ²)

Результаты исследований.

В результате расчетов установлено, что генеральная совокупность данных является однородной. При доверительной вероятности оценки данных, равной 0,95, доверительный интервал не превышает 2 %.

Определены математические ожидания общей мощности в месяц, только в рабочие дни и только в выходные и праздничные дни за май-август 2016 г. (рис.1). При этом наибольшая общая средняя мощность потреблялась в июне, наименьшая в июле. Средняя общая мощность в июне больше потребляемой мощности в июле на 30,3 %. Наибольшее среднее значение мощности в рабочие дни соответствует маю, а наименьшее среднее значение — июлю. Отличие в средних значениях мощности при этом составляет 37,73 %. Потребляемая средняя мощность в выходные и праздничные дни за четыре месяца изменяется незначительно (не более 10 %).

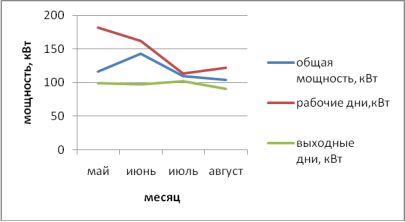
Рис. 1. Изменение среднего значения потребляемой мощности в июне-августе 2016 г.

Дисперсия и среднее квадратическое отклонение значений мощности по месяцам года значительно изменяются (рис. 2). Наибольшее значение среднего квадратического отклонения соответствует июню, а наименьшее значению — маю. Разница составляет 58,741 кВт. При анализе только рабочих дней значение среднего квадратического отклонения составило наибольшее в мае (109,31 кВт), а наименьшее в августе — (23,25 кВт). В четыре раза меньше.

Для выходных дней среднее квадратическое отклонение значений мощности изменяется от 6,26 кВт до 35,60 кВт (в 5,7 раз). Аналогично изменяется и дисперсия.

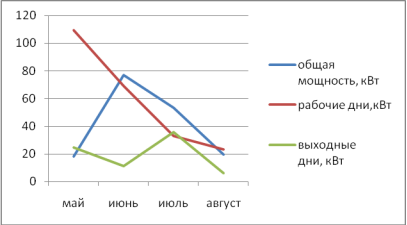
Рис. 2. Изменение среднего квадратического отклонения значений потребляемой мощности

Характер изменения коэффициента вариации ν по виду аналогичен изменению среднего квадратичного отклонения (рис. 2). Его значение изменяется от 0,16 до 0,54 при анализе данных нагрузок по месяцам и составляет от 0,19 до 0,51 — в рабочие, а в выходные дни от 0,069 до 0,35.

Максимальное значение общей нагрузки соответствует 0,86 относительных единиц, минимальное значение — 0,1. Максимальная общая нагрузка в мае-августе превышает минимальную общую нагрузку в 8,6 раз (рис. 3). Для рабочих дней максимальная нагрузка превышает минимальную в 5–8 раз, а в выходные дни в 2,2–2,7 раза. Таким образом, минимальная нагрузка Р_мин = (12,5 –20) % Р_мах.

Суточные графики нагрузки аппроксимированы полиномиальной функцией и получены уравнения, описывающие изменение мощности Р^* во времени t.

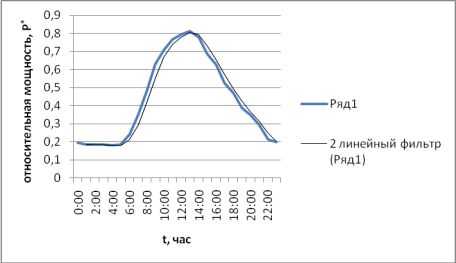
Рис. 3. График нагрузок и линия тренда за май 2016 года в относительных величинах

Полиномиальная функция наиболее удачно описывает величины, переменно возрастающие и убывающие. Она подходит для такой нестабильной величины как электрическая нагрузка. Уравнение 5-ой степени полиномиальной линии тренда нагрузок за май 2016 года имеет вид:

Р^* = 7E-07t^5–1E-05t^4–0,0001t³ + 0,021t^2–0,109t + 0,311.

Коэффициент достоверности аппроксимации χ² = 0,95, показывает степень соответствия трендовой модели исходным данным. Коэффициент достоверности аппроксимации близок к единице. Оценочное прогнозируемое значение имеет малое отклонение от фактического значения (менее 5 %).

Изменение нагрузки, за все дни каждого месяца (май-август), представляет собой резко переменный график (рис. 4) с увеличением нагрузки в дневное время рабочих дней и малыми значениями ее в ночное время и в выходные и праздничные дни. При этом максимальная нагрузка составляет 0,857 о.е., а минимальная нагрузка — 0,106 о.е. Минимальная нагрузка составляет Р_мин = 12,4 %Р_мах.

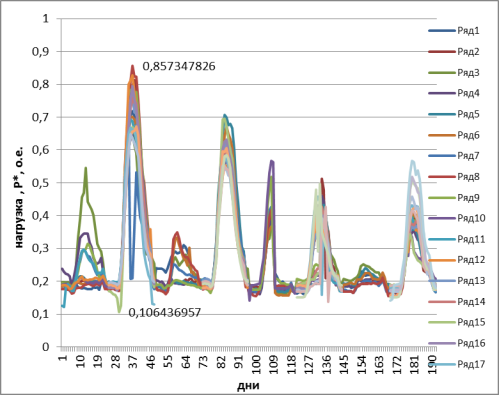
Рис. 4. График нагрузок за май-август 2016 года в относительных величинах

В выходные дни с мая по август 2016 года максимальная нагрузка составляет 0,568 о.е., а минимальная нагрузка — 0,122о.е., то есть Р_мин = 21,4 % Р_мах. В рабочие дни максимальная нагрузка равна 0,857 о.е., а минимальная — 0,106 о.е. Максимальная нагрузка больше минимальной в 8,1 раз и определяется только рабочими днями.

Выводы.

1. Графики электрических нагрузок РГРТУ за май-август 2016 года облегчают отслеживание колебаний уровня напряжения, и позволяют прогнозировать возможные скачки нагрузки.
2. Генеральная совокупность статистических данных является однородной. При доверительной вероятности оценки данных, равной 0,95, доверительный интервал не превышает 2 %.
3. Наибольшая общая средняя мощность потреблялась в июне, наименьшая — в июле. В июне она на 30,3 % больше потребляемой в июле.
4. Наибольшее среднее значение мощности в рабочие дни в мае, а наименьшее в июле. Разница составляет 37,73 %. Потребляемая средняя мощность в выходные и праздничные дни за четыре месяца изменяется незначительно (не более 10 %).
5. Наибольшее значение среднего квадратического отклонения общей нагрузки в июне, наименьшее в мае. Разница — 58,741 кВт. Для рабочих дней значение среднего квадратического отклонения наибольшее в мае (109,31кВт), а наименьшее значение в августе — (23,25 кВт). Для выходных дней среднее квадратическое отклонение значений мощности изменяется от 6,26 кВт до 35,60 кВт, (в 5,7 раз). Изменение дисперсии и коэффициента вариации аналогичное.
6. Графики суточной нагрузки характеризуются максимальным значением общей нагрузки в месяц, равной 0,86 о.е., минимальным значением — 0,1о.е., Максимальная общая нагрузка в мае-августе превышает минимальную нагрузку в 8,6 раз. Для рабочих дней превышение максимальной нагрузки над минимальной в 5–8 раз, а в выходные дни — 2,2–2,7 раз. Минимальная нагрузка Р_мин = (12,5–20) % Р_мах.

Литература:

1. Федоров А. А. Теоретические основы электроснабжения промышленных предприятий. — М.: Энергия, 1976, 272 с.
2. Васильева Т. Н. Надежность электрооборудования и систем электроснабжения. — М.: Горячая линия — Телеком, 2014. — 152 с.: ил.
3. Вентцель Е. С. Теория вероятностей. — М.: Наука, 1969. – 576 с.
4. Электроснабжение сельского хозяйства/ Лещинская Т. Б., Наумов И. В. — М.: Колос С, 2015. — 655 с.