The article describes the practical application of the graph theory, shows the application of the shortest-path finding algorithm, uses program realization to find a solution, finds the most economical way to get from one point to another.
Key words: analysis, graph theory, Bellman-Ford algorithm, shortest-path finding algorithm, program realization
Nowadays society is at the stage when a trip to another country or to another city is not difficult. The turnover is made within not one particular city, but the country or even around the hole world. Freight transport is a part of everyday life not only for professional companies, but also for ordinary citizens: they send parcels to other regions, buy goods from other cities and from abroad. People also often travel from one city to another. Also different companies have to spend a lot of money to pay for travel of their employees to other cities. In this paper, we consider such an urgent problem at the moment, as the savings in civilian intercity trips, particularly on trains. As a continuation and improvement of practical application of this work in the future, we plan to take into consideration not only civil trip, but also freight transport. To study is taken the route from Samara to Moscow. All possible routes of trains are represented as a graph, where the vertices — stations, fins — path between stations, rib weight — ticket price from one station to another.
One can get from Samara to Moscow by selecting one of the three trains: № 55, № 121E and № 131U. [1] Contemplated in the paper stations are shown in the Table 1:
Table 1
Contemplated stations
|
1. Samara |
8. Sizran |
15. Bazarnya |
22. Chaadaevka |
28. Potma |
|
2. Novokuibyshevsk |
9. Kuzovatovo |
16. Inza |
23. Kadoshkino |
29. Zubova Polyana |
|
3. Bezenchuk |
10. Novospasskoe |
17. Kuznetsk |
24. Ruzaevka |
30. Belinskaya |
|
4. Chapaevsk |
11. Barish |
18. Nochka |
25. Penza |
31. Pachelma |
|
5. Obsharovki |
12. Klyuchiki |
19. Sura |
26. Kovylkino |
32. Sasovo |
|
6. Ryazan |
13. Bashmakovo |
20. Sosedka |
27. Vernadovka |
33. Morshansk |
|
7. Verda |
14. Ryazhsk |
21. Moscow |
Green route — train № 55, yellow — № 131U, orange — № 121E.
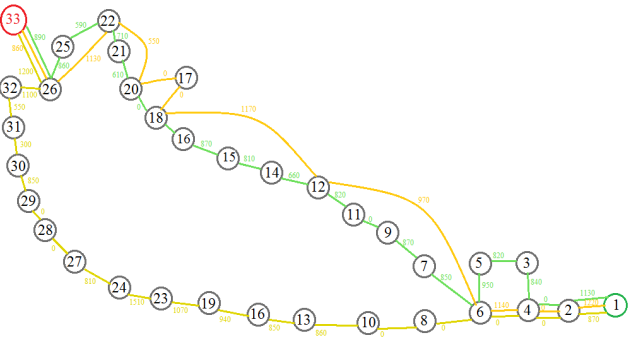
Fig. 1. Graph train routes
Top number 1 (Samara) must be connected by edges with all (Table 2).
Table 2
Weights of edges from the first top
|
1–2: 1130 |
1–8: 1280 |
1–18: 1240 |
1–26: 2510 |
|
1–2: 1220 |
1–9: 1220 |
1–19: 1630 |
1–27: 1860 |
|
1–2: 920 |
1–10: 1210 |
1–20: 1370 |
1–28: 1820 |
|
1–3: 1130 |
1–11: 1170 |
1–20: 1590 |
1–29: 1910 |
|
1–4: 1090 |
1–12: 1000 |
1–21: 1420 |
1–30: 2020 |
|
1–4: 1140 |
1–12: 1220 |
1–22: 1440 |
1–31: 2140 |
|
1–4: 890 |
1–13: 1450 |
1–22: 2030 |
1–32: 2170 |
|
1–5: 900 |
1–14: 1170 |
1–23: 1690 |
1–33: 3250 |
|
1–6: 930 |
1–15: 1120 |
1–24: 1970 |
1–33: 2800 |
|
1–6: 1000 |
1–16: 1440 |
1–25: 1490 |
1–33: 2950 |
|
1–6: 620 |
1–17: 1340 |
1–26: 2120 |
|
|
1–7: 930 |
1–18: 1650 |
1–26: 2030 |
And draw edges from all the vertices to the top № 33 (Moscow) (Table 3).
Table 3
Weights of edges in the last vertex
|
1–33: 3250 |
6–33: 2700 |
16–33: 2400 |
25–33: 1310 |
|
1–33: 2800 |
6–33: 2770 |
17–33: 1430 |
26–33: 890 |
|
1–33: 2950 |
7–33: 2700 |
18–33: 1810 |
26–33: 860 |
|
2–33: 3250 |
8–33: 2770 |
18–33: 1900 |
26–33: 1200 |
|
2–33: 2730 |
9–33: 2800 |
19–33: 2400 |
27–33: 1910 |
|
2–33: 2950 |
10–33: 2590 |
20–33: 1810 |
28–33: 1910 |
|
3–33: 3250 |
11–33: 2230 |
20–33: 1420 |
29–33: 1660 |
|
4–33: 3250 |
12–33: 2100 |
21–33: 1520 |
30–33: 1730 |
|
4–33: 2710 |
12–33: 1950 |
22–33: 1360 |
31–33: 1520 |
|
4–33: 2950 |
13–33: 2590 |
22–33: 1400 |
32–33: 1770 |
|
5–33: 2730 |
14–33: 2010 |
23–33: 2100 |
|
|
6–33: 3250 |
15–33: 3100 |
24–33: 1840 |
All data is entered. Bellman — Ford algorithm is used as a way of finding a solution: the search algorithm of finding the shortest path in a weighted graph [2]. It finds the shortest path from one vertex to all others. Software implementation is made independently. The pseudo-code of the algorithm is as follows:
for v V
do d [v] 
d [s] 
0
for i
1 to |V| — 1
do for (u, v) E
if d [v] > d [u] + (u, v) then d [v] d [u]+(u,v)
return d; [3]
By applying the algorithm to a graph problem, a solution is that the cheapest trip will cost 2770 rubles (Figure 2). It should be noted that straight tickets from 1 to 33 vertex cost 3250, 2800 and 2950 respectively.
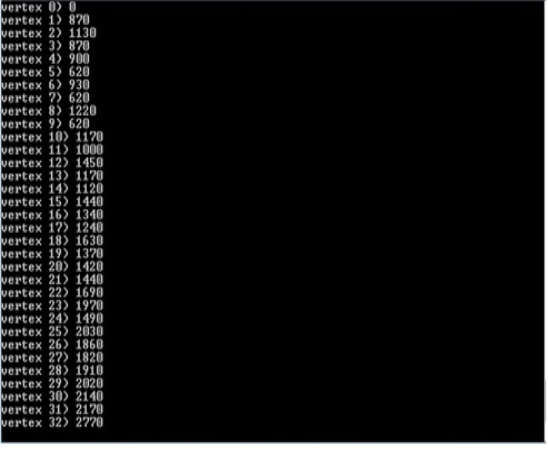
Fig. 2. Search software solutions
The route of the resulting solution will be as follows:
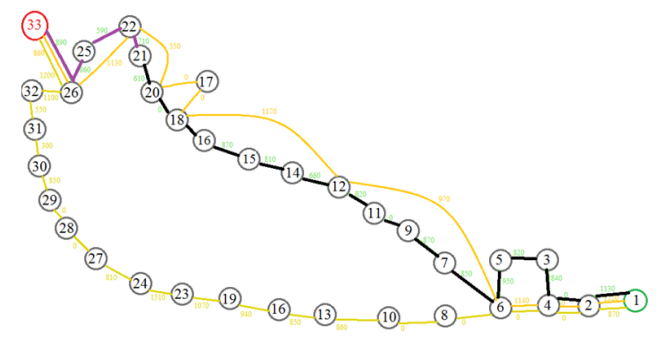Fig. 3. The resulting route
Thus, you need get from 1 to 21 top, there you must change trains and get to the final top.
To summarize, it must be said that it was clearly considered the application of graph theory on practice. In particular, it was found the most economical way to get from Samara to Moscow by the train. Solution process fully demonstrates the effectiveness of the view model as a graph and the practical application of the algorithm of finding the shortest paths, specifically the Bellman-Ford algorithm. Saving turned a relatively small, but with the increase in the number of people who need to get from one point to another, its value increases and becomes noticeable, which is important for large companies, as it allows them to reduce costs and expenses. In the future, the problem will be discussed with respect to transportation. It is clear that to carry one kilogram load savings would be small, but with the weight increasing for tens or hundreds of tons, rather large values can be obtained that companies can save by applying the only representation of the model in the form of a graph and elementary shortest-path finding algorithm.
References:
- The site «Russian Railways» — www.rzd.ru access mode.
- Basaker R., T. Saaty. Finite graphs and networks. — M.: Nauka, 1974. 368 s.
- Belov V. V., Vorobyov E. M., V. E. Shatalov. Theory grafov. – M., 1976. 392 s.
