Одним из классических методов изучения спектра линейного оператора ![]() в комплексном гильбертовом пространстве
в комплексном гильбертовом пространстве ![]() с областью определения
с областью определения ![]() является изучение его числовой области значений:
является изучение его числовой области значений:
![]() .
.
Это понятие впервые введено в работе [1] и доказано, что числовой образ матрицы содержит все ее собственные значения. Вслед за этим это понятие обобщено разными способами, см. например [2,3].
Рассмотрим интегральный оператор ![]() , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве ![]() квадратично-интегрируемых (комплекснозначных) функций, определенных на
квадратично-интегрируемых (комплекснозначных) функций, определенных на ![]() по формуле
по формуле
![]() ,
, ![]() .
.
Легко можно проверить, что оператор ![]() , действующий в гильбертовом пространстве
, действующий в гильбертовом пространстве ![]() , ограничен и самосопряжен.
, ограничен и самосопряжен.
Лемма. Число ![]() является бесконечно кратным собственным значением оператора
является бесконечно кратным собственным значением оператора ![]() .
.
Доказательство. Рассмотрим уравнение
![]() .
.
Оно эквивалентно уравнению
Положим
![]() .
.
Здесь число ![]() выбирается из условия
выбирается из условия
![]() .
.
Простые вычисления показывают, что
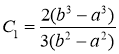 .
.
Таким образом, функция
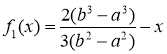
удовлетворяет условию (1). Положим
![]() .
.
Здесь число
![]() .
.
Простые вычисления показывают, что
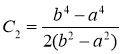 .
.
Следовательно, функция
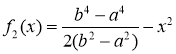
удовлетворяет условию (1). Далее, для любого натурального числа ![]() положим
положим
![]() ,
,
где константа ![]() найдется из условия
найдется из условия
![]() .
.
Обсуждая аналогично, имеем
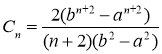 .
.
Полученная последовательность функций ![]() линейно независимо. Это означает, что число
линейно независимо. Это означает, что число ![]() является бесконечно кратным собственным значением оператора
является бесконечно кратным собственным значением оператора ![]() . Лемма доказана.
. Лемма доказана.
Теперь изучаем дискретный спектр оператора ![]() . С этой целью рассмотрим уравнение для собственных значений, т. е.
. С этой целью рассмотрим уравнение для собственных значений, т. е.
![]() .
.
Это уравнение записывается в следующем виде:
![]() . (2)
. (2)
Так как ![]() из равенства (2) для
из равенства (2) для ![]() находим
находим
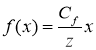 , (3)
, (3)
где
![]() . (4)
. (4)
Подставляя полученное выражение (3) в равенства (4) имеем, что число
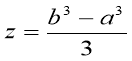
является простым собственным значением оператора ![]() .
.
Отсюда следует, что
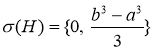 .
.
Верна следующая теорема.
Теорема. Для числового образа ![]() оператора
оператора ![]() имеет место равенство
имеет место равенство
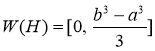 .
.
Литература:
- O. Toeplitz. Das algebraische Analogon zu einem Satze von Fejer // Math. Z., — 1918, — V. 2, — no. 1–2, — P. 187–197.
- H. Langer, A. S. Markus, V. I. Matsaev, C. Tretter. A new concept for block operator matrices: the quadratic numerical range // Linear Algebra Appl., — 2001, — V. 330, — no. 1–3, P. 89–112.
- L. Rodman, I. M. Spitkovsky. Ratio numerical ranges of operators // Integr. Equ. Oper. Theory, — 2011, V. 71, — P. 245–257.







