Пусть ![]() . Рассмотрим вещественнозначную аналитическую функцию
. Рассмотрим вещественнозначную аналитическую функцию ![]() на
на ![]() . Получен одно важное представление для этой функции.
. Получен одно важное представление для этой функции.
Условие 1. Функция ![]() является четной по совокупности переменных
является четной по совокупности переменных ![]() , (
, (![]() ), имеет единственный невырожденный минимум в точке
), имеет единственный невырожденный минимум в точке ![]() и существуют положительно определенная матрица
и существуют положительно определенная матрица ![]() , числа
, числа ![]() такие, что
такие, что
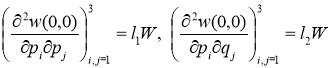 .
.
Замечание. Условия 1 выполняется в случае, когда
![]() ,
,
где
![]() .
.
Действительно, простые вычисления показывают, что
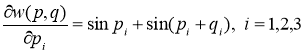 ;
;
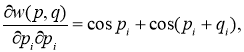
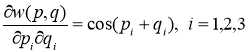 ;
;
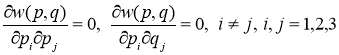 .
.
Поэтому
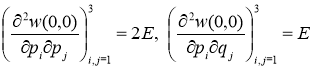 ,
,
где ![]() единичная матрица размера
единичная матрица размера ![]() .
.
Положим
![]() и
и ![]() .
.
Теорема 1. Пусть выполняется условия 1. Тогда существует некоторая ![]() -окрестность
-окрестность ![]() точки
точки ![]() такая, что имеет место равенство
такая, что имеет место равенство
![]()
и ![]() . Здесь функция
. Здесь функция ![]() удовлетворяет условию
удовлетворяет условию
![]() (1)
(1)
для некоторого ![]() .
.
Доказательство. Так как функция
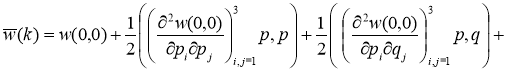
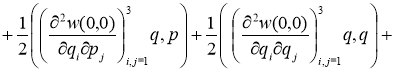
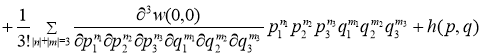
для каждого ![]() , где
, где
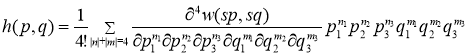 (2)
(2)
и ![]() - положительные числа,
- положительные числа, ![]() .
.
Функция ![]() - чётна, следовательно,
- чётна, следовательно,
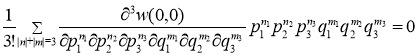 .
.
Функция ![]() - аналитична, поэтому [1] существует положительное число
- аналитична, поэтому [1] существует положительное число ![]() , ограничивающее все частные производные 4-порядка функции
, ограничивающее все частные производные 4-порядка функции ![]() , именно,
, именно,
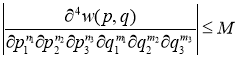
для каждого
![]() .
.
Так как ![]() - симметричен, т.e.
- симметричен, т.e. ![]() , получим
, получим
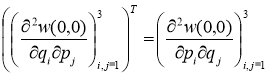
(где ![]() означает транспонированную матрицу).
означает транспонированную матрицу).
Поэтому
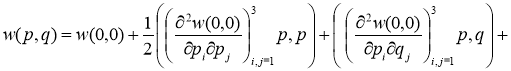
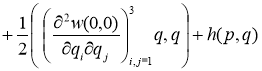
По условию 1
![]()
и матрица
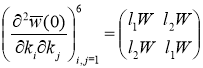
положительно определена. Отсюда следует, что ![]() и, следовательно,
и, следовательно, ![]() . Теорема 1 доказана.
. Теорема 1 доказана.
Теорема 1 играет важную роль при изучении поведении определителя Фредгольма соответствующий модели Фридрихса.
Литература:
- В. А. Зорич. Математический анализ. Часть I. Изд-во ФАЗИС, Москва, 1997.







