Свойства коммутаторов на *-подалгебрах в алгебрах локально измеримых операторов

В работе рассматриваются свойства коммутаторов и тройные лиевые дифференцирований, действующих на идеальных *-подалгебрах в алгебрах LS(M) локально измеримых операторов, присоединенных к алгебре фон Неймана M. Даются также достаточные условия на тип алгебры фон Неймана M, обеспечивающие ассоциативность всех тройных лиевых дифференцирований на .

Пусть произвольная ассоциативная алгебра над полем комплексных чисел. Линейный оператор называется ассоциативным дифференцированием на алгебре , если для любых . Если a ∈ A, то отображение D_a: A → A, определенное равенством D_a(x) = ax — xa = [a, x], x ∈ A, является дифференцированием на A. Дифференцирования вида D_a называются внутренними дифференцированиями.

Говорят, что линейный оператор L: A → A есть лиевое дифференцирование на алгебре , если L([x, y]) = [L(x), y] + [x,L(y)] для всех x, y ∈ A. Каждое ассоциативное дифференцирование D: A → A, очевидно, является лиевым дифференцированием.

Примером лиевого неассоциативного дифференцирования служит центрозначный след E:→ Z(), т. е. такое линейное отображение E из алгебры со значениями в центре Z() алгебры , для которого E(xy) = E(yx) при всех x, y ∈.

Линейный оператор называется тройной лиево дифференцированием на алгебре ,если

.

Хорошо известно, что любое тройной лиево дифференцирование L на алгебре фон Неймана имеет стандартной формы, т. е. имеет вид , где -ассоциативное дифференцирование на и -центрозначный след на .

В случае, когда A является алгеброй фон Неймана, стандартная форма тройного лиевого дифференцирования имеет вид L = Da + E для некоторого A. Развитие теории алгебр S(M) измеримых операторов и алгебр LS(M) локально измеримых операторов, присоединненных к алгебрам фон Неймана или AW* алгебрам M, дало возможность строить и изучать новые содержательные примеры *-алгебр неограниченных операторов. Одной из интересных задач здесь стала проблема описания всех дифференцирований, действующих в S(M). В случае коммутативных алгебр фон Неймана M верно равенство S(M) = LS(M) и что любое дифференцирование в S(M) является внутренним, т. е. нулевым, тогда и только тогда, когда M — атомическая алгебра. Для коммутативных AW* — алгебр M критерием существования ненулевых дифференцирований в S(M) служит отсутствие свойства -дистрибутивности у булевой алгебры всех проекторов из M. Для алгебр фон Неймана M типа I, все дифференцирования на алгебрах LS(M) и S(M) были описаны в [1].

Замкнутый линейный оператор , присоединенный к , называется измеримым относительно алгебры фон Неймана , если — сильно плотно в . Множество всех операторов, измеримых относительно , является * — алгеброй с единицей над полем относительно операций сильного сложения, сильного умножения и перехода к сопряженному оператору, (умножение на скаляры определяется обычным образом, при этом, считается, что . Замкнутый линейный оператор , присоединенный к , называется локально измеримым относительно алгебры фон Неймана , если существует такая последовательность центральных проекторов из , что и для всех . Множество всех локально измеримых относительно операторов также образует *-алгебру с единицей 1 относительно операций сильного сложения, сильного умножения и перехода к сопряженному оператору, при этом, и есть *-подалгебры в . Центр в * — алгебре совпадает с *-алгеброй , и в случае когда — фактор, либо — конечная алгебры фон Неймана, всегда верно равенство .

Теорема 1. Пусть - алгебра фон Неймана типа типа I, либо типа III. — идеальная *-подалгебра в содержащая . Тогда каждое тройной лиево дифференцирование представляется в виде , где -внутреннее дифференцирование на а --значный след на .

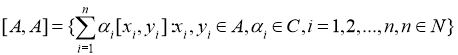
для алгебр фон Неймана, имеющих тип I.

Теорема 2. (см. [2]) Если M — алгебра фон Неймана типа I и A- идеальная * — подалгебра в LS(M), M A, то [A, A] = A.

Иеет место следующая

Теорема 3. Пусть M- алгебра фон Неймана, имеющая тип I, A идеальная *-подалгебра в LS(M), M A. Тогда любое тройной лиево дифференцирование в A является ассоциативным дифференцированием.

Замечание. Если M имеет тип I, A — *- подалгебра в LS(M) и 1 A. Тогда [A,A] это означает, что LS(M) = S(M) = Mat(n,S(Z(M)) существуют тройные лиевые дифференцирования, которые не являются ассоциативными диффеnренцированиями. Таковым является, например след 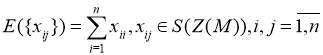который, очевидно, есть тройной лиево дифференцирование, однако E не является ассоциативным дифференцированием, поскольку E(1) 0.

Литература:

1. S. Albeverio, Sh. A. Ayupov, K. K. Kudaybergenov, Structure of derivations on various algebras of measurable operators for type I von Neumann algebras, J. Func. Anal. 256 (2009), 2917–2943.
2. Чилин В. И., Жураев И. М. Коммутаторы локально измеримых операторов, присоединенных к алгебре фон Неймана типа I, Материалы Республиканской научной конференции. Ургенч. 9–10 ноября 2012. Т. II. С. 122–124.
3. Чилин В. И., Жураев И. М. Аддитивные лиевые дифференцирования на алгебрах локально измеримых операторов, Материалы Республиканской научной конференции. Ташкент. 20–24 май 2013. С. 256–258.