Приводятся алгоритмы устойчиво оценивания параметров динамических объектов управления на основе методов регуляризации.
The firm estimation algorithms of the dynamic object control parameters are given on the basic of regularization methods.
Рассмотрим следующее входо-выходное соответствие описываемое линейным разностным уравнением,
y(t)+ ![]() (1)
(1)
Где е(t) — белый шум,
Поскольку в это уравнение белый шум e(t) входит как его непосредственная ошибка модель (1) часто называют структурой модели ошибки уравнения [1–3] В этом случае имеется следующий набор настраиваемых параметров:
![]() .
.
Если ввести
![]() (q)=1+
(q)=1+![]() …+
…+![]() ,
,
B(q)=
То соответствующие операторы по задающему и возмущающему воздействием приму вид
G(q,![]() =
=![]() , H(q
, H(q![]() .
.
Теперь введем вектор
![]()
Тогда можно записать
![]() |
| ![]()
Для оценивания параметров ![]() будем использовать взвешенный критерий
будем использовать взвешенный критерий
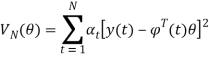 . (2)
. (2)
Обозначив диагональную матрицу
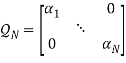 , (3)
, (3)
Критерий (2) можно переписать в виде
![]() . (4)
. (4)
Нетрудно проверить что минимум достигается при значении аргумента
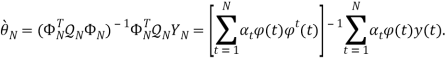 (5)
(5)
Произведем факторизацию![]() :
:
![]() ,
,
Где ![]() — нижняя треугольная матрица с единицами на диагонали:
— нижняя треугольная матрица с единицами на диагонали:
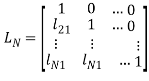 ,
,
а ![]() -диагональная матрица как в (3),Тогда (4)принимает вид
-диагональная матрица как в (3),Тогда (4)принимает вид
![]()
Элементы этих матриц равны
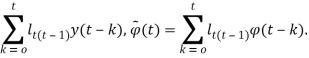
Таких образом, имеем
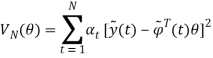 ,
,
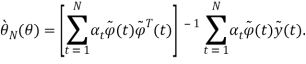
Чтобы исследовать свойства оценки ![]() допустим, что действительные измерения y(t) (t= 1,…..,N) могут быть описаны равенством
допустим, что действительные измерения y(t) (t= 1,…..,N) могут быть описаны равенством
y(t)=![]() (6)
(6)
Где![]() } — некоторая последовательность возмущений,
} — некоторая последовательность возмущений,
Если обозначить
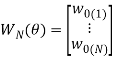
Можно записать (6) как
![]()
![]()
Подставляя это выражение в (5), получаем
![]()
![]() (7)
(7)
где
![]()
что в случае![]() записывается также в виде
записывается также в виде
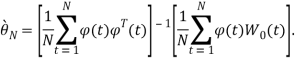
Это выражение для ошибки по параметру имеет чисто алгебраическую природу и справедливо для произвольных последовательностей {![]() }.
}.
![]() (8)
(8)
Так как ![]() и
и ![]() — детерминированные легко вычислить математическое ожидание (8):
— детерминированные легко вычислить математическое ожидание (8):
E![]() =
=![]() (9)
(9)
Тогда имеем
E
Это равенство озночает, что оценки ![]() являются несмещенными.Для отклонения оценки параметра от среднего получаем из (8), (9):
являются несмещенными.Для отклонения оценки параметра от среднего получаем из (8), (9):
![]() (10)
(10)
Откуда получаем матрицу ковариаций
Cov![]() (11)
(11)
Анализируя основные уравнения (7),(8) параметрическое оценивания и уравнения (9),(10) и (11) для математическое ожидания, отклонения оценки параметра от среднего значения и ковариации на основе взвешенного критерия (2) можно видеть что при их вычислении используется обратная матрица вида ![]() .Матрица
.Матрица ![]() может быть плохо обусловленной т. е. малым изменениям исходных данных могут отвечать большие изменение решения. Отмеченное обстоятельство при использовании уравнений (7), (8) приводит к необходимости применения методов регуляризации [4, 5].
может быть плохо обусловленной т. е. малым изменениям исходных данных могут отвечать большие изменение решения. Отмеченное обстоятельство при использовании уравнений (7), (8) приводит к необходимости применения методов регуляризации [4, 5].
Тогда искомое решение![]() на основе (8) с использованием регуляризации необходимо вычислять в виде
на основе (8) с использованием регуляризации необходимо вычислять в виде
![]() , i=0,1,2,…, 0< Ξ < 1,
, i=0,1,2,…, 0< Ξ < 1,
Где >0 — параметры регуляризации, Е- единичная матрица.
Если погрешности исходных данных уравнения (8) неизвестны или их вычисление сопряжено со значительными трудностями, то параметр регуляризации целесообразно определять либо на основе способа квазиоптимальности:
Или отношений [5]:
Где
![]() ,
, ![]() ,
,
K=![]() f=
f=![]() .
.
Применение приведенных регулярных процедур способствует повышению точности решения задачи параметрической идентификации объектов управления.
Литература:
- Каминскас В.Идентификация динамических систем по дискретнымнаблюдениям.-Вилбнюс:Келас,1982–338с.
- Кашьяп Р.А, Рао А. Р. Построение динамических моделей по экспериментальным данным. Пер. с англ. –М.: наука,1983.-384 с.
- ЛьюнгЛ.Идентификация систем. Теория для пользователья/пер, с англ,/Под ред. Я. З. Цқпкина.-М.: Наука. 1991,,-432 с.
- Тихонов А. Н., Арсенин В. Я. Методы решения некорректных задач. –М.: Наука, 1979. -285 с.
- Воскобойников Ю. Е., Преображенский Н.Г, Седельников А.И, Математическая обработка эксперимента в молекулярной газодинамике.-Новосибирск:Наука.1984.







