Оценка прочности деревянных конструкций с учетом масштабного фактора



Преимущества древесины как строительного материала в сложных климатических условиях северо-Арктического региона очевидны. Это природный, относительно легкий, экологически чистый материал, обладающий низкий теплопроводностью.

При деформировании образцов из древесины следует учитывать не только влияние неоднородной структуры, но и напряжения, возникающие вследствие наличия этой неоднородности.

Так как распределение неоднородностей в объеме изделия имеет статистическую природу, то и распределение указанных дополнительных напряжений должно иметь статистический характер, что порождает масштабный эффект в нагруженных образцах. Несмотря на то, что явление имеет большое практическое значение, природа «масштабного фактора» до сих пор не выяснена.

Имеется несколько теорий, из которых ни одна не получила соответствующего экспериментального обоснования.

Статистическая теория впервые выдвинута А. П. Александровым и С. Н. Журковым. [1] Проявление масштабного фактора они связывали с наличием дефектов в образцах.

В крупных образцах вероятность встретить наиболее опасный дефект является более высокой, чем в малых. Минимальную прочность крупного образца авторы считают равной прочности наиболее слабого из мелких образцов. Было замечено, что снижению масштабного эффекта способствует также уменьшение скорости нагружения. Само явление было названо авторами масштабным эффектом при хрупком разрыве, поскольку испытаниям подвергались хрупкие стеклонити.

Статистическая теория Т. А. Конторовой даёт количественную зависимость между размером неоднородности и прочностью образца, отождествляя упругую энергию, обусловленную присутствием неоднородности, с поверхностной энергией области, занятой неоднородностью. [2]

Статистическая теория Н. А. Афанасьева похожа на теорию Т. А. Конторовой, но рассматривается она применительно к усталости металлов [3].

В этой работе автор делает вывод о том, что металлы, чувствительные к концентрации напряжений, при переменной нагрузке малочувствительны к изменению размеров и наоборот.

Исследования В. Ю. Гольцева и др. [4] позволили заметить, что увеличение толщины элементов металлических конструкций приводят к повышению степени опасности хрупкого разрушения. Это связано с возрастанием стеснения деформации по толщине с увеличением её, с малым смягчением процесса нагружения имеющихся и образующихся дефектов и усилением вследствие этого объёмного напряженного состояния.

По-видимому, для каждого материала характерна некоторая оптимальная толщина, при которой может быть получено максимальное сопротивление разрушению.

Анализ различных работ свидетельствует о том, что пока нет единой точки зрения на природу масштабного эффекта. В зависимости от того, что принимают за критическое состояние, справедливы могут быть разные гипотезы, но ни одна из них не может претендовать на универсальность.

Нашей задачей является проверка наличия масштабного эффекта при растяжении элементов из чистой древесины.

Испытано на растяжение 60 образцов, имеющих длину 400 мм и сечения 50x4, 50x5, 50x7, 50x8, 50x10 и 50x12 мм.

Результаты эксперимента приведены в таблице.

Таблица 1

Значения прочности древесины при растяжении вдоль волокон

№п/п	Сечение образца, мм	n, шт	М, МПа	±σ, МПа	m, МПа	V,%	р,%
1	50х4	20	64	9,0	2,0	14,0	3,1
2	50х5	20	61	11,7	2,6	19,2	4,2
3	50х7	20	51	8,6	1,9	17,6	3,7
4	50х8	20	47	6,4	1,51	13,6	3,0
5	50х10	20	42	8,5	1,89	20,2	4,5
6	50х12	20	38	7,01	1,55	18,4	4,1

Примечание:

n — число наблюдений,

М — среднее арифметическое,

σ — среднее квадратическое отклонение,

V — вариационный коэффициент,

р — показатель точности.

Чем меньше показатель точности, тем надежнее результаты исследования. Принято считать, что в области деревянных конструкций достаточная надежность эксперимента будет обеспечена только в том случае, если показатель точности не превышает 5. В нашем случае это условие выполняется, то есть эксперимент надежный.

Из эксперимента выяснено, что наблюдается явная тенденция уменьшения предела прочности древесины при растяжении по мере роста размеров образцов. По этим результатам построен график на рис. 1.

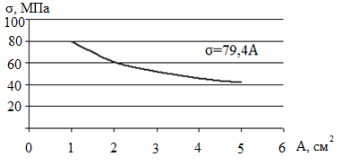
Рис. 1. Зависимость прочности при растяжении малых чистых образцов от площади поперечного сечения

В результате дисперсионного анализа установлено, что влияние случайных факторов можно считать несущественным по сравнению с влиянием основного масштабного фактора. При сечении от 2 см² до 3 см² увеличение сечения на 1 см² дает уменьшение прочности на 10 МПа, при сечении 3…4 см² это же приращение площади уменьшает прочность на 9 МПа, а при сечении 4…5 см^{2 —} всего на 6 МПа.

В дальнейшем исследовались образцы натуральных размеров. Испытывались доски длиной 3 м и сечением 160х40, 180х50, 180х80 см.

Замечено что при увеличении площади поперечного сечения на 1 см² прочность уменьшается в среднем на 0,12 МПа.

В ходе регрессионного анализа было выявлено, что корреляционное отношение равно 0,4, а отношение к его ошибке больше 4, т. е. оно является достоверным, связь между двумя свойствами в этом случае считается доказанной (рис. 2).

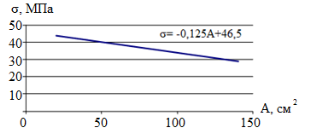
Рис. 2. Зависимость прочности на растяжение образцов натуральных размеров от площади поперечного сечения

Исследования показали, что, несмотря на то, что плотность более крупных размеров была больше, прочность с увеличением размеров уменьшается. Регрессионный анализ определил, что существует очень малая корреляция между прочностью и размерами образца. Коэффициент корреляции равен 0,34.

Увеличение площади на 1 см² уменьшает прочность на 0,2 МПа. На основании вышесказанного можно утверждать, что при больших сечениях изменение площади поперечного сечения сказывается в небольшой степени на прочности при растяжении, т. е. масштабный фактор можно не принимать во внимание.

Древесина является природным материалом, содержащим различные дефекты строения. В конструкциях практически отсутствуют элементы из чистой древесины. Поэтому в дальнейшем необходимо изучить влияние масштабного фактора на прочность элементов, содержащих пороки строения.

Испытаны на растяжение образцы размерами 50х5 мм, 50х12мм длиной 400мм, а также доски 150х38мм и 150х50мм с сучками центральными и выходящими на кромку. Размеры сучков соответствовали 2 сорту пиломатериалов.

На рис.3 приводятся графики зависимости прочности от площади сечения элементов.

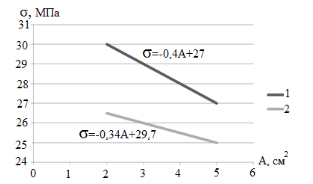
Рис. 3. Зависимость прочности при растяжении малых образцов с сучками от площади поперечного сечения

Примечание:

1. Образцы с центральными сучками.
2. Образцы с кромочными сучками.

Замечено, что в сучковатых малых образцах изменение размеров незначительно влияет на прочность. При увеличении площади сечения на 1 см² прочность падает всего на 2 МПа. Решающее значение здесь имеет не размер сечения, а сам сортообразующий порок.

В образцах строительных размеров замечено почти одинаковое понижение прочности, как при наличии сучков, так и при их отсутствии. Это объясняется тем, что в крупных элементах, кроме сучков, существует вероятность встречи других дефектов, внутренних неоднородностей, которые могут оказать решающее влияние на прочность.

Таким образом, в сечениях строительных размеров прочность понижена вследствие преимущественного влияния статистического фактора, в малых образцах из-за наличия порока строения. Это позволяет допустить, что исследования влияния пороков строения на прочность деревянных элементов при растяжении возможно на малых образцах, что значительно упрощает эксперимент и сэкономит материал.

Литература:

1. Александров А. П., Журков С. Н. Явление хрупкого разрыва. — М. Госуд. Технико-теорет. Изд-во, 1993, 51с.
2. Конторова Т. А. Статистическая теория прочности. — Журнал техн. физики, 1940, т. X, вып. 11, с. 91–95.
3. Афанасьев Н. Н. Статистическая теория прочности. — Журнал технической физики, 1941, т X, вып. 12, с. 126–139.
4. Гольцев В. Ю. и др. Влияние толщины металлических материалов на их способность тормозить разрушение. — Заводская лаборатория, 1969, т XXXV, № 10 с. 1237–1241.