Статья посвящена алгоритмизации обучения математики в колледже. Через алгоритмизацию обучения преподаватель добивается целенаправленной работы по осуществлению достаточно гибкой системы последовательных шагов для перехода от незнания к знанию, от неумения к умению, применять теоретические знания на практике. Приводится пример алгоритма при решении математической задачи.
Ключевые слова: алгоритмизация, эффективность, алгоритм, учебно-информационное взаимодействие.
The article is devoted algorithmization teaching mathematics in college. Through teacher training algorithmization seeking purposeful work to implement the system flexible enough consecutive steps for the transition from ignorance to knowledge, from inability to ability to apply theoretical knowledge in practice. An example of an algorithm for solving a mathematical problem.
Keywords: algorithmization efficiency algorithm. educational and informational interaction.
Современные формы обучения, инновации в преподавании, введение новых технологий диктуют преподавателю необходимость постигать секреты мастерства, а значит, и совершенствовать методы обучения и воспитания обучающихся.
Современный этап развития общества характеризуется внедрением информационных технологий во все сферы человеческой деятельности. Новые информационные технологии оказывают существенное влияние и на сферу образования. Происходящие фундаментальные изменения в системе образования вызваны новым пониманием целей, образовательных ценностей, а также необходимостью использования новых технологий обучения. Поэтому одной из дидактических задач в колледже является формирование мышления обучающегося, развитие его интеллекта. Важной составляющей интеллектуального развития человека является алгоритмизация мышления [1, с. 135].
Навыки алгоритмизации мышления способствуют также формированию особого стиля культуры человека, составляющими которого являются: целеустремленность и сосредоточенность, объективность и точность, логичность и последовательность в планировании и выполнении своих действий, умение четко и лаконично выражать свои мысли, правильно ставить задачу и находить окончательные пути ее решения, быстро ориентироваться в стремительном потоке информации.
Алгоритмизация уровня обучающихся–введение понятия алгоритма и формирование его основных свойств.
– алгоритм – это общепонятное и однозначное предписание, которое определяет последовательность действий, позволяющее достичь искомый результат. Алгоритмизация предполагает жесткое выполнение шагов, а прием дает общее направление деятельности по решению разных задач, не регламентируя каждый шаг. Такой подход к преподаванию математики в колледже определяет условия для формирования у обучающихся навыков, позволяющих успешно изучать на первом курсе базовый курс «математики». Применение алгоритмов на первом курсеявляется твердым фундаментом для активизации самостоятельной и творческой работы обучающихся.
В настоящее время алгоритмизация обучения математики в колледже имеет основные подходы к организации самостоятельной учебной деятельности студентов: контролируемая самостоятельная работа, управляемая самостоятельная работа и самообразование. Они отличаются друг от друга по двум критериям: активности субъектов образовательного процесса и осознанности участия в учебной деятельности.
Самостоятельная работа студентов – это многообразные виды индивидуальной и коллективной деятельности студентов, осуществляемые под руководством, но без непосредственного участия преподавателя в специально отведенное для этого аудиторное и неаудиторное время.
Усиление самостоятельной работы студентов, увеличение её объёма в структуре учебных планов и программ обуславливается также рядом научно-педагогических и организационно-методических требований к модернизации образовательного процесса. Во-первых, организация самостоятельной работы студентов способствует личностно-ориентированной направленности профессиональной подготовки студентов, развитию у студентов способности к самообучению. Во-вторых, расширение доли самостоятельной работы студентов придаёт в большей мере учебному процессу проблемно-исследовательский характер, поскольку происходит более активное вовлечение студентов в самостоятельное решение целостной системы заданий, имеющих профессиональную направленность и возрастающий уровень сложности. В-третьих, именно самостоятельная работа студента обеспечивает саморазвитие необходимых способностей будущего специалиста к более сложным видам деятельности, способы и содержание, которой не могут передаваться или осваиваться по образцам. В-четвёртых, повышение роли самостоятельной работы студентов предполагает создание соответствующих условий для её организации, усиление ответственности, как студентов, так и преподавателей за результаты своей деятельности, учебного процесса в целом.
На первых курсах для студентов колледжа задача становится разнообразней и содержательней, появляется возможность включать упражнения разного типа и уровня сложности, предполагающая, что приемы деятельности могут быть разной степени сложности и обобщенности. Они состоят из большого числа действий, выполнение которых приводит к применению алгоритмов на отдельных этапах работы.
Алгоритмизация обучений применяется в разных смыслах: 1) как составляющая методологической основы математики; 2) как обучение способам деятельности; 3) как обучение различным действиям, адекватным содержанию обучения математике; 4) как учебная деятельность [2, с. 287].
Для построения алгоритма нужно проанализировать содержание и цели обучения, деятельность обучающихся по его усвоению, деятельность преподавателя по организации этого усвоения с использованием компьютерной среды обучения. Построенный алгоритм обучения должен быть осуществим не только теоретически, но и практически, учитывать особенности студентов данной группы. Примерами алгоритмов обучения математике могут служить: обучение доказательству теорем, обучение решению задач и другие. На основе этих результатов определены обучения математики с ее использованием для алгоритмизации и роль задачи как средства обучения математической деятельности [3, с. 24].
![]() Пример: Решение тригонометрических неравенств.
Пример: Решение тригонометрических неравенств.
На занятии математики рассмотрим неравенства вида sint>a, где -1≤а≤1.
Составим алгоритм решения.
1. Если аргумент — сложный (отличен от х), то заменяем его на t.
2. Строим в одной координатной плоскости t Oy графики функций y=sint и y=a.
3. Находим такие две соседние точки пересечения графиков (поближе к оси Оу), между которыми синусоида располагается вышепрямой у=а. Находим абсциссы этих точек.
4. Записываем двойное неравенство для аргумента t, учитывая период синуса (t будет между найденными абсциссами).
5. Делаем обратную замену (возвращаемся к первоначальному аргументу) и выражаем значение х из двойного неравенства, записываем ответ в виде числового промежутка.
Решаем первое неравенство:
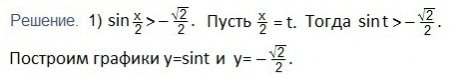
Построение графика синуса рассмотрим «решение тригонометрических неравенств»
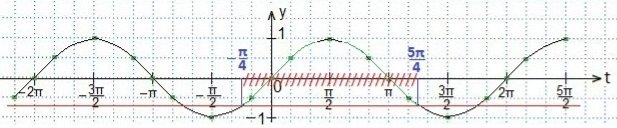
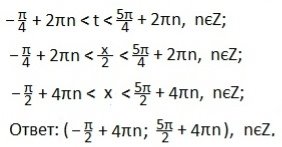
Учитывая периодичность функции синуса, запишем двойное неравенство для значений аргумента t, удовлетворяющие последнему неравенству. Вернемся к первоначальной переменной. Преобразуем полученное двойное неравенство и выразим переменную х. Ответ запишем в виде промежутка.
Решаем второе неравенство:
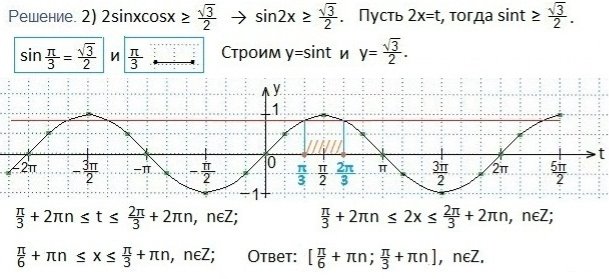
При решении второго неравенства нам пришлось преобразовать левую часть данного неравенства по формуле синуса двойного аргумента, чтобы получить неравенство вида: sint≥a. Далее следуем алгоритму.
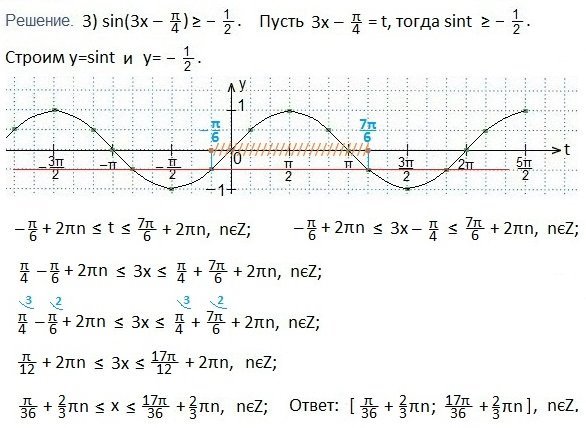
Решаем третье неравенство:
Одним из главных условий успешной направленности в обучении математическим дисциплинам в колледже является повышение алгоритмизацииприменения с учетом основных тенденций практики использования информационных технологий в современном обществе. Алгоритмизация применения является той частью математической культуры, которая способствует формированию и развитию специальных представлений, связанных с понятием алгоритма. Под алгоритмом принято понимать совокупность специфических «алгоритмических» представлений и навыков, которые на современном этапе развития общества должны составлять часть общей культуры каждого человека и, следовательно, определять целенаправленный компонент профессионального образования. С развитием информационных технологий в обучении получит эффективную алгоритмизацию. Алгоритмизация в обучении математике обеспечивает учебно-информационное взаимодействие на основе применения алгоритмов решения различных задач с использованием современных программных средств.
Повышение применения алгоритмизация развивает динамичность мышления, его гибкость, формирует умение разделять сложный объект на простые составляющие, определять взаимосвязи между ними. Все это необходимо для изучения и позволяет научиться такому подходу к любой задаче. Умение представить свои рассуждения и весь ход решения задачи в виде алгоритма существенно дисциплинирует мышление студентов и становится необходимым практическим качеством специалиста в любой профессии. В профессиональном плане эти навыки помогут более быстрому и сознательному овладению профессией [2, с. 289]. Для подготовки студентов, способных реализовывать любые задачи с использованием новейшего программного обеспечения, необходимо формировать алгоритмизацию с самого начала обучения. Развитие алгоритмических навыков при решении математических задач в настоящее время необходимо и в связи с появлением математических расчетов определенного уровня алгоритмического мышления.
Литература:
- Лучко, Лариса Геннадьевна. Диссертация. Формирование алгоритмической культуры учащихся в процессе обучения базовому курсу информатики. Омск, 1999. – 152 с.
- Акамова Н. В., Буданова Н. А. Алгоритмический метод обучения математике с использованием новых информационных технологий в среднем специальном учебном заведении // Молодой ученый. — 2010. — №10. — С. 285-289.
- Торогелдиева К. М. Применение математических задач как средства обучения (кырг). Бишкек, 2015. – 117 с.







