Как известно, некоторые актуальные задачи, в частности, задачи квантовой механики, статистической механики и гидродинамики сводятся к исследованию спектра модели Фридрихса [1–3].
Введем оператор ![]() модели Фридрихса, действующий в
модели Фридрихса, действующий в ![]() , как
, как
![]() ,
,
где операторы ![]() и
и ![]() определяются по правилам
определяются по правилам
![]() ,
,
![]() .
.
Здесь ![]() –положительное действительное число, а функция
–положительное действительное число, а функция ![]() имеет вид
имеет вид
![]() ,
,
![]() .
.
При этих предположениях оператор
В настоящей работе изучаем некоторые спектральные свойства модели Фридрихса ![]() .
.
Возмущение ![]() оператора
оператора ![]() является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр
является самосопряженным одномерным оператором. Из известной теоремы Вейля [4] о сохранении существенного спектра при возмущениях конечного ранга вытекает, что существенный спектр ![]() оператора
оператора ![]() совпадает с существенным спектром оператора
совпадает с существенным спектром оператора ![]() . Известно, что
. Известно, что
![]() ,
,
где числа ![]() и
и ![]() определяются равенствами
определяются равенствами
![]() ,
,
![]() .
.
Следовательно,
![]() .
.
Пусть ![]() –комплексная плоскость. Для любого
–комплексная плоскость. Для любого ![]() определим аналитическую функцию
определим аналитическую функцию ![]() (детерминант Фредгольма, ассоциированный с оператором
(детерминант Фредгольма, ассоциированный с оператором ![]() ):
):
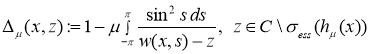 .
.
Теперь установим связь между собственными значениями оператора
Теорема 1. При каждом фиксированном ![]() оператор
оператор ![]() имеет собственное значение
имеет собственное значение ![]() тогда и только тогда, когда
тогда и только тогда, когда ![]() .
.
Доказательство. Пусть число ![]() есть собственное значение оператора
есть собственное значение оператора ![]() , а
, а ![]() –соответствующая собственная функция. Тогда функция
–соответствующая собственная функция. Тогда функция ![]() удовлетворяет уравнению
удовлетворяет уравнению
![]() . (1)
. (1)
Заметим, что для любых ![]() и
и ![]() имеет место соотношение
имеет место соотношение ![]() . Тогда из уравнения (1) для
. Тогда из уравнения (1) для ![]() имеем
имеем
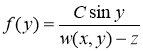 , (2)
, (2)
где
![]() . (3)
. (3)
Подставляя выражение (2) для ![]() в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
в равенства (3), получим, что уравнение (1) имеет ненулевое решение тогда и только тогда, когда
![]() ,
,
т. е. когда
Теорема 1 доказана.
Из теоремы 1 вытекает следующее:
![]() .
.
Из определения функции ![]() видно, что при всех
видно, что при всех ![]() имеет место неравенство
имеет место неравенство ![]() . В силу теоремы 1 это означает, что для любого
. В силу теоремы 1 это означает, что для любого ![]() оператор
оператор ![]() не имеет собственных значений в интервале
не имеет собственных значений в интервале ![]() . Из монотонности функции
. Из монотонности функции ![]() в интервале
в интервале ![]() имеем, что для любого
имеем, что для любого ![]() оператор
оператор ![]() имеет не более одного собственного значения в интервале
имеет не более одного собственного значения в интервале ![]() . Если
. Если ![]() при некотором
при некотором ![]() , то оператор
, то оператор ![]() имеет единственное простое собственное значение в интервале
имеет единственное простое собственное значение в интервале ![]() .
.
Литература:
- Л. Д. Фаддеев. О модели Фридрихса в теории возмущений непрерывного спектра. Труды мат. инс-та АН СССР, Т. 73, М.: Наука, 1964, С. 292–313.
- Р. А. Минлос, Я. Г. Синай. Исследование спектров стохастических операторов, возникающих в решетчатых моделях газа. ТМФ, 1979, Т. 2, № 2. С. 230–243.
- Е. М. Дынкин, С. Н. Набако, С. И. Яковлев. Границы конечности сингулярного спектра в самосопряженной модели Фридрихса. Алгебра и анализ. Т. 3, № 2, 1991, С. 77–90.
- М.Рид, Б.Саймон. Методы современной математической физики. Т.4. Анализ операторов. М.: Мир, 1982.







