Методика расчета параметров СКСЭ и СЭ ГОНП



Хорошо известно, что современные энергоносители, такие как газ, нефть и уголь, не бесконечны. К тому же их использование зачастую наносит непоправимый вред окружающей среде и, соответственно, ухудшает жизнь человека. Одним из основных решений двух обозначенных выше проблем является производство солнечных панелей, поскольку солнечная энергия является экологически чистой.

На данный момент одними из самых перспективных типов солнечных элементов являются сенсибилизированные красителем солнечные элементы (СКСЭ) и солнечные элементы на основе гибридных органо-неорганических перовскитов (ГОНП). Оба типа солнечных ячеек могут быть частично оптимизированы одним и тем же способом.

В данной работе представлен теоретический способ оптимизации параметров сенсибилизированным красителем солнечных элементов (СКСЭ). Рассмотрена природа полупроводника диоксида титана TiO₂ и красителя, а также влияние различных технологических параметров на эффективность СКСЭ. Методика основана на решении краевой задачи методом пристрелки.

В результате были получены зависимости плотности тока и эффективности от времени жизни электронов и толщины слоя диоксида титана. Также была получена вольт-амперная характеристика СКСЭ.

Полученные результаты были проанализированы и было выяснено, что оптимальная толщина слоя диоксида титана d = 15 нм, при этом дальнейшее увеличение приводит к незначительному уменьшению производительности СКСЭ. Показано также влияние времени жизни электронов. Значения свыше 40–50 мс не приводят к увеличению производительности СКСЭ.

Технология и материалы, используемые для третьего поколения солнечных элементов (СЭ), таких как сенсибилизированные красителем солнечные элементы (СКСЭ), солнечные элементы на основе гибридных органо-неорганических перовскитов (ГОНП), дают возможности для получения солнечных элементов с высокой эффективностью [1]. Уменьшить кол-во источников. СКСЭ на основе наноструктурированного красителя и пористого металлооксида привлекают значительное внимание со времен работы Рейгана и Гретцеля [2], поскольку их производство экологично и энергоэффективно. На данный момент сообщается, что коммерческие СКСЭ имеют эффективность, равную 11 %, а образцы, тестируемые в лабораториях, — 15 % [3]. Поскольку при изготовлении СКСЭ используются дешевые материалы и простые методы получения, их производство выходит намного дешевле, чем у солнечных элементов на основе кремния.

Оптимизация параметров СКСЭ требует лучшего соотношения между взаимосвязанными процессами переноса и накопления электронов в металлооксиде и рекомбинацией электронов [4].

Описанная в статье методика расчета представлена с целью оптимизации параметров производительности СКСЭ. С помощью данной методики расчета были получены и рассмотреныплотность тока короткого замыкания , напряжение холостого хода , фактор заполнения FF, а также эффективность энергетического преобразования . Также в данной статье проанализировано влияние толщины слоя диоксида титана и времени жизни электронов на производительность СКСЭ.

Физическая модель и методика расчета

В работе используется классическая структура СКСЭ, которая представлена на рисунке 1. Элемент содержит два электрода, представляющих собой стеклянную подложку с нанесенным прозрачным проводящим покрытием из диоксида олова, легированного сурьмой или фтором. Фоточувствительный электрод (фотоэлектрод) покрыт слоем пористого диоксида титана, который в свою очередь обогащен красителем (рутением). На противоэлектрод нанесен тонкий слой платины, который выступает в качестве катализатора для окислительно-восстановительных реакций. Пространство между двумя электродами заполнено электролитом, содержащим окислительно-восстановительную пару йодид/трийодид (I^-/I₃^-).

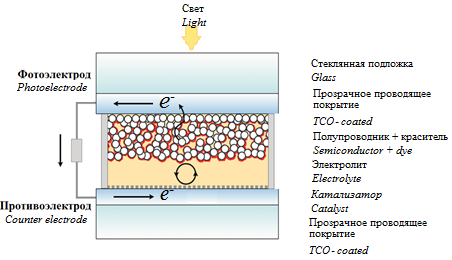
Рис. 1. Структура СКСЭ

Когда на СКСЭ падает солнечный свет, электроны из молекулы красителя переходят в возбужденное состояние и инжектирует в зону проводимости TiO₂, после чего собирается на электроде и уходит во внешнюю цепь. Положительный заряд (катионы красителя) уменьшается путем приема электрона от иона йодида (I^-), который восстанавливается путем уменьшения числа ионов трийодида (I₃^-) на противоэлектроде.

При использовании наноструктурированного диоксида титана процесс истощения будет менее выражен, так что влияние обратного электрического поля незначительно [5]. Возникновение фотонапряжения объясняется встроенным потенциальным барьером между TiO₂ и ППП и/или изменением уровня Ферми из-за инжекции электронов. Наиболее вероятный процесс рекомбинации имеет место между электронами из TiO₂ и ионами I₃^- [6].

В идеальном случае скорость поглощения фотонов в единице объема может быть записана как:

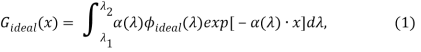
где описывается положением внутри слоя TiO₂ толщиной , включая краситель, — длина волны.

В реальном случае скорость поглощения фотонов света в единице объема уменьшается до . Это связано с поглощением и отражением света на фотоэлектроде. Для описания этих процессов вводится поправочный коэффициент с целью разработки упрощенной модели для расчета и оптимизации любого типа СКСЭ. Тогда:

Скорость инжекции электронов зависит от коэффициента эффективности инжекции [4], тогда:

В представленной модели перенос электрического заряда чисто диффузионный, следовательно, он может быть описан уравнением диффузионного переноса для плотности электрического тока J [7] Внутреннее электрическое поле, вызванное несбалансированным локальным зарядом, имеет крайне малую величину, и им можно пренебречь [8]. Плотность электронов n(x) в зоне проводимости TiO₂ описывается уравнением непрерывности в. В таком случае система уравнений примет следующий вид:

где e — заряд электрона, x — положение внутри слоя TiO₂ толщиной , R(x) — скорость рекомбинации, D — коэффициент диффузии электронов.

В данной статье решено пренебречь ловушками захвата электронов, поэтому в уравнении (4) данные величины не представлены. Также считается, что процесс рекомбинации происходит между электронами в зоне проводимости слоя TiO₂ и анионами в электролите [6]. Следовательно, скорость рекомбинации пропорциональна , тогда:

где — начальная концентрация, а – время жизни электрона.

Граничные положения будут следующие:

1. Предполагая, что электроны, отвечающие граничному положению x = 0, тогда:

где — плотность состояний в зоне проводимости TiO₂:

где — эффективная масса электрона, – постоянная Больцмана, h — постоянная Планка, T — температура, — энергия между зоной проводимости и квазиуровнем Ферми.

2. Предполагая, что все электроны собраны на границе x=d (слой TiO₂ хорошего качества, и внутри него процессы рекомбинации отсутствуют), тогда граничное состояние при x=d:

Напряжение холостого хода, полученное при J=0, определяется следующим образом:

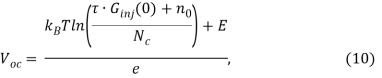
где — скорость инжекции электронов при x=0.

Система дифференциальных уравнений (4) и (5) вместе с граничными состояниями (7) и (9) имеют недостаточно состояний при х=0, но имеют граничные состояния при x=d (9). Эта проблема известна под названием «проблема граничных величин» и определяется дифференциальными уравнениями, в которых некоторые состояния заданы в начальной точке, в то время как другие заданы в конечной точке. Для решения этой системы уравнений используется метод пристрелки. Данный метод заключается в задании различных величин в промежутке от x=0 до x=d.

Данная методика расчета рассматривает основные процессы, которые происходят в реальных СКСЭ, и упрощает другие, такие как поглощение и отражение света на фотоэлектроде, введением поправочного коэффициента для получения .

Литература:

1. H. S. Jung and J. K. Lee, “Dye sensitized solar cells for economically viable photovoltaic systems,” The Journal of Physical Chemistry Letters, vol. 4, no. 10, pp. 1682–1693, 2013.
2. A. Yella, H.-W. Lee, H. N. Tsao et al., “Porphyrin-sensitized solar cells with cobalt (II/III)-based redox electrolyte exceed 12 percent efficiency,” Science, vol. 334, no. 6056, pp. 629–634, 2011.
3. M. Grätzel, “Dye-sensitized solar cells,” Journal of Photochemistry and Photobiology C, vol. 4, no. 2, pp. 145–153, 2003.
4. J. Ferber, R. Stangl, and J. Luther, “Electrical model of the dye-sensitized solar cell,”Solar Energy Materials and Solar Cells, vol. 53, no. 1–2, pp. 29–54, 1998.
5. J. Bisquert and I. Mora-Seró, “Simulation of steady-state characteristics of dye-sensitized solar cells and the interpretation of the diffusion length,” Journal of Physical Chemistry Letters, vol. 1, no. 1, pp. 450–456, 2010.
6. S. Wenger, M. Schmid, G. Rothenberger, A. Gentsch, M. Grätzel, and J. O. Schumacher, “Coupled optical and electronic modeling of dye-sensitized solar cells for steady-state parameter extraction,” Journal of Physical Chemistry C, vol. 115, no. 20, pp. 10218–10229, 2011.
7. S. Wenger, M. Schmid, G. Rothenberger, A. Gentsch, M. Grätzel, and J. O. Schumacher, “Coupled optical and electronic modeling of dye-sensitized solar cells for steady-state parameter extraction,” Journal of Physical Chemistry C, vol. 115, no. 20, pp. 10218–10229, 2011.
8. J. Ferber, R. Stangl, and J. Luther, “Electrical model of the dye-sensitized solar cell,”Solar Energy Materials and Solar Cells, vol. 53, no. 1–2, pp. 29–54, 1998.