Расчет параметров солнечных элементов СКСЭ и ГОНП



В данной работе использована методика расчета для получения вольтамперных характеристик СКСЭ на основе рутениевого красителя. Однако методика может быть применена к СКСЭ на основе любого другого красителя. Коэффициент поглощения рутениевого красителя в диапазоне от до и другие параметры и константы взяты из источников [1,4,8, 9] и представлены в таблице 1.

Таблица 1

Параметры иконстанты, использованные вмодели

	5.6 ()
T	300 K
	0.9 эВ
	0.95
D

На рисунке 2 представлена вольтамперная характеристика, полученная в зависимости от времени жизни электрона при толщине d=20 нм и = 0.9.

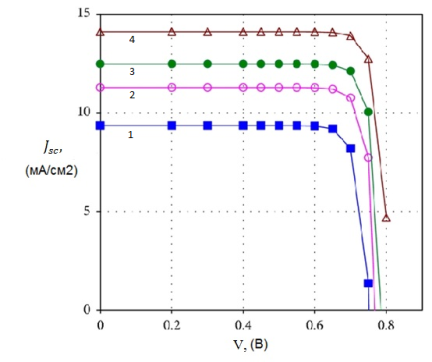
Рис. 2. Вольтамперная характеристика СКСЭ () в зависимости от времени жизни электрона

1 — 2 — ; 3 — ; 4 —

Таблица 2

Значения и

		мВ		,%
0.8	11.170	819	0.828	7.572
0.9	12.470	822	0.858	8.482
0.95	13.120	823	0.827	8.937
1	13.770	824	0.827	9.392

Из таблицы 2 видно, что при увеличении , растет плотность тока короткого замыкания, а вместе с ним и энергоэффективность СКСЭ, тогда как напряжение холостого хода и фактор заполнения остаются практически неизменными.

На рисунках 3а и 3б изображены зависимости и [2,3]. Видно, что толщина данного слоя является важнейшим технологическим параметром, определяющим плотность тока короткого замыкания и энергоэффективность СКСЭ. Плотность тока короткого замыкания и энергоэффективность СКСЭ достигают максимальных значений в интервале от d=15 нм до d=20 нм [8,11]. Дальнейшее увеличение толщины приводит к уменьшению значений и эффективности СКСЭ. Также следует отметить, что толщина слоя TiO₂ практически не влияет на напряжение холостого хода и фактор заполнения.

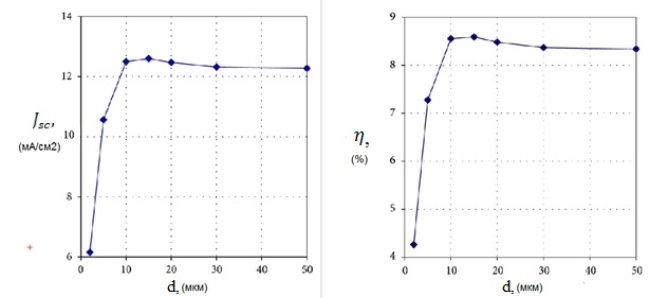
Рис. 3а, 3б. График зависимости плотности тока от толщины и коэффициента энергоэффективности от толщины

Кривые, изображенные на рисунках 4 (а) и 4 (б), отвечают значениям плотности тока короткого замыкания и энергоэффективности СКСЭ соответственно в зависимости от времени жизни электрона.

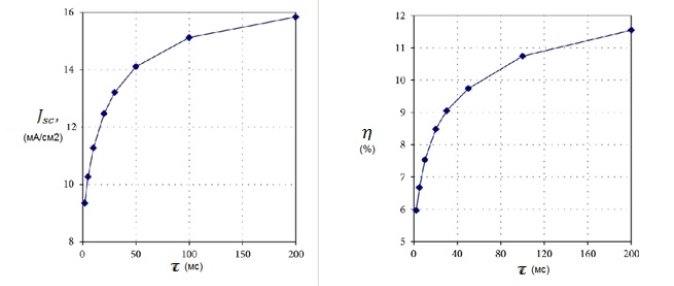
Рис 4а, 4б. График зависимости плотности тока от толщины и коэффициента энергоэффективности от

Полученные величины и согласуются с уже описанными ранее в литературе значениями для данного типа СКСЭ [5, 6, 7, 10, 12]. Следовательно, предложенная методика расчета является рабочей и гибкой, поэтому она может быть использована для проектирования и оптимизации СКСЭ.

Предложенная в данной статье методика расчета, позволяющая оптимизировать параметры любого типа СКСЭ, состоит из упрощенной физической модели и численного метода, допускающего решение системы дифференциальных уравнений, полученных из этой модели.

Применение данной методики позволило определить вольтамперные характеристики СКСЭ на основе рутения и рассчитать и . Полученные результаты согласуются с описанными в литературе значениями. Также проанализировано влияние материала полупроводника и красителя и различных технологических параметров на производительность СКСЭ. Продемонстрировано, что оптимальная толщина слоя диоксида титана d = 15 нм, при этом дальнейшее увеличение приводит к незначительному уменьшению производительности СКСЭ. Показано также влияние времени жизни электрона. Значения свыше 40–50 мс не приводят к увеличению производительности СКСЭ.

Таким образом, предложенная в данной статье методика расчета позволяет проводить комплексный анализ производительности СКСЭ и допускает дальнейшее развитие численных методов для проектирования и оптимизации любых типов СКСЭ.

Литература:

1. H. S. Jung and J. K. Lee, “Dye sensitized solar cells for economically viable photovoltaic systems,” The Journal of Physical Chemistry Letters, vol. 4, no. 10, pp. 1682–1693, 2013.
2. A. Yella, H.-W. Lee, H. N. Tsao et al., “Porphyrin-sensitized solar cells with cobalt (II/III)-based redox electrolyte exceed 12 percent efficiency,” Science, vol. 334, no. 6056, pp. 629–634, 2011.
3. M. Grätzel, “Dye-sensitized solar cells,” Journal of Photochemistry and Photobiology C, vol. 4, no. 2, pp. 145–153, 2003.
4. J. Ferber, R. Stangl, and J. Luther, “Electrical model of the dye-sensitized solar cell,”Solar Energy Materials and Solar Cells, vol. 53, no. 1–2, pp. 29–54, 1998.
5. J. Bisquert and I. Mora-Seró, “Simulation of steady-state characteristics of dye-sensitized solar cells and the interpretation of the diffusion length,” Journal of Physical Chemistry Letters, vol. 1, no. 1, pp. 450–456, 2010.
6. S. Wenger, M. Schmid, G. Rothenberger, A. Gentsch, M. Grätzel, and J. O. Schumacher, “Coupled optical and electronic modeling of dye-sensitized solar cells for steady-state parameter extraction,” Journal of Physical Chemistry C, vol. 115, no. 20, pp. 10218–10229, 2011.
7. S. Wenger, M. Schmid, G. Rothenberger, A. Gentsch, M. Grätzel, and J. O. Schumacher, “Coupled optical and electronic modeling of dye-sensitized solar cells for steady-state parameter extraction,” Journal of Physical Chemistry C, vol. 115, no. 20, pp. 10218–10229, 2011.
8. J. Ferber, R. Stangl, and J. Luther, “Electrical model of the dye-sensitized solar cell,”Solar Energy Materials and Solar Cells, vol. 53, no. 1–2, pp. 29–54, 1998.
9. P. H. Joshi, D. P. Korfiatis, S. F. Potamianou, and K. A. Th. Thoma, “Optimum oxide thickness for dye-sensitized solar cells-effect of porosity and porous size: a numerical approach,” Ionics, vol. 19, no. 3, pp. 571–576, 2013.
10. D. Gentilini, A. Gagliardi, and A. D. Carlo, “Dye solar cells efficiency maps: a parametric study,” Optical and Quantum Electronics, vol. 44, no. 3–5, pp. 155–160, 2012.
11. Liling G., Zhang S., Guanghui Z., Xing Li, Hanxing L. Synthesis and Characterization of Layered Perovskite-type organic-inorganic hybrids ((R-NH3)2(CH3NH3)Pb2I7), Journal of Wuhan university of technology-mater. Sci. Ed. — 2012
12. Silvia C., Edoardo M., Paolo F., Andrea L., Francesco G., MAPbI3.xClx mixed halide perovskite for hybrid solar cells: the role of chloride as dopant on the transport and structural properties, Chem. Mater. — 2013 — P.4613–4618.