Сегодня в условиях модернизации содержания начального общего образования и внедрения новых стандартов начального общего образования идет широкое обсуждение необходимости создания новых подходов к проектированию учебных заданий, для правильной оценки результатов обучения. Ведущим методом в исследовании данной проблемы является метод проектирования учебных заданий по математике начальной школы.
Ключевые слова: учебные задания, математика, метапредметные универсальные учебные действия, начальная школа
Следуя требованиям новых стандартов, педагог должен овладеть методами и приемами составления учебных заданий, позволяющих оценивать не только предметные, но и метапредметные и личностные образовательные результаты обучающегося на различных этапах образовательного процесса [2, c. 280].
В математическое содержание начальной школы желательно включать задачи метапредметной направленности, т. е. задачи реальных ситуаций, которые в свою очередь будут мотивировать обучающихся к дальнейшему изучению математики в целом и ее разделов.
Деятельность обучающихся определяется через формулировку заданий, поэтому в учебный процесс желательно включать задания, в формулировке которых требуется: проанализировать, доказать (объяснить), сравнить, создать схему или модель, продолжите, обобщите (сделайте вывод), выберите решение или способ решения, исследуйте, оцените, измените, придумайте.
При проектировании задач необходимо учитывать уровни усвоения учебного материала. Каждому уровню усвоения учебного материала соответствуют свои вопросы. Учитель, тонко разбираясь в вопросах разных типов, может управлять процессом познания на каждом из уровней, выстраивать обучение так, чтобы новые знания проходили последовательно через уровни понимания, использования, анализа, синтеза, позволяли бы ребенку становиться личностью через выработку его жизненной (субъектной) позиции [3, c. 123].
Современные требования к образованию предусматривают реализацию Федерального государственного образования начального общего образования (ФГОС НОО).
Данные требования должны выполняться в процессе учебного процесса в рамках всех учебных дисциплин, желательно при выполнении учебных заданий на каждом уроке.
В рамках данной работы мы рассмотрели учебно-методический комплекс «Перспектива» авторы В. Г. Дорофеев и др. Данный комплекс был проанализирован на эффективность реализации ФГОС НОО.
За основу анализа возьмем 2 класс выше указанного комплекса. Приведем, примеры заданий из учебника, которые демонстрируют в основном предметную направленность.
Рассмотрим задачу 2 (рис. 1) из выше указанного учебника.

Рис. 1. Задача 2
Приведём примеры аналогичных задач, направленные на умение планировать свою деятельность, в соответствии с поставленной задачей (регулятивные универсальные учебные действия).
Пример 1. Составьте алгоритм построения отрезка ВГ.
Пример 2. Укажи цифрами от 1 до 4 последовательность действий для построения отрезка ВГ:
– с помощью линейки соединить точки В и Г,
– отметить точку Г,
– отложить от точки В вправо шесть клеток и вверх две клетки,
– отметить точку В.
Рассмотрим следующий пример на умение самостоятельно осуществлять контроль учебной деятельности.
Пример 3. Укажите какая из девочек верно указала план построения отрезка ВГ.
А также согласно указанным ниже критериям оцените деятельность девочек.
Критерии оценивания:
Выполнено верно — 2 балла.
Допущена 1 ошибка — 1 баллов.
|
Светлана – соединить точки В и Г, – отметить точку Г, – отложить от точки В вправо шесть клеток и вверх две клетки, – отметить точку В. |
Ольга – отметить точку В, – отметить точку Г, – отложить от точки В вправо шесть клеток и вверх две клетки, – с помощью линейки соединить точки В и Г. |
Анна – отметить точку В, – отложить от точки В вправо шесть клеток и вверх две клетки, – отметить точку Г, – с помощью линейки соединить точки В и Г. |
Рассмотрим следующий пример на умение задавать и отвечать на вопросы.
Пример 4. Составьте алгоритм построения отрезка ВГ. Обсудите с другом составленный алгоритм.
Рассмотрим задачу 5 из учебника (Рис 2).
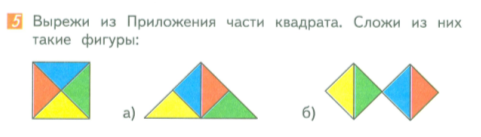
Рис. 2. Задача 5
Данная задача не заставляет детей думать, анализировать, рассуждать, т. е. задача направлена составление заранее заданных фигур.
Предложим другой вариант задачи, направленный на коммуникацию и сотрудничество.
Пример 5. Вырежите из приложения части квадрата, подумайте и обсудите с другом возможность составления из всех частей квадрата:
а) треугольника,
б) двух квадратов.
Рассмотрим задачу 7 из учебника (рис. 3).
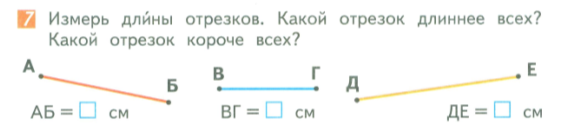
Рис. 3. Задача 7
Предложим другую интерпретацию данного задания.
Пример 6. Начертите в тетрадях три отрезка АБ, ВГ и ДЕ. Выпишите длины этих отрезков. Укажите самый длинный отрезок и самый короткий.
Комментарий. В данной составленной задаче дети самостоятельно пытаются построить данные отрезки, т. е. проявляют самостоятельность, измеряют и анализируют полученные результаты измерений.
Далее рассмотрим задачу на умение использовать знаково-символические средства для создания моделей изучаемых объектов / процессов, для решения задач.
Пример 7. Рассмотрите рисунок к басне И. А. Крылова «Лебедь, Щука и Рак». Составьте геометрическую модель к данному рисунку.

Рис. 4. Лебедь, Щука и Рак
Пример 8. Оформите в тетрадях геометрические модели следующих углов: АБВ, ГДЕ, ЖЗИ.
Следующая задача 6 из учебника (рис. 5) заставляет детей думай, проявить смекалку, т. к. решением данной задачи получаются множество углов, которое с первого взгляда детям трудно увидеть.
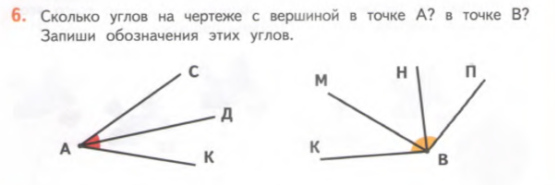
Рис. 5. Задача 6
Следующая задача 10 (рис. 6) из учебника похожа на предыдущую, учащимся сложно разглядеть скрытые геометрические фигуры, такие задачи можно давать на физкультминутках, чтобы дети в свободном режиме от учебы обсудили решение данной задачи в виде дискуссии, предложили свои решения, возможно организовать в виде игры «кто больше увидел геометрических фигур?». Такие задачи дают возможность детям аргументировать свое решение, отстоять свою точку зрения, прислушаться к решению других ребят, в случае ошибочного решения принять решение одноклассника или учителя.
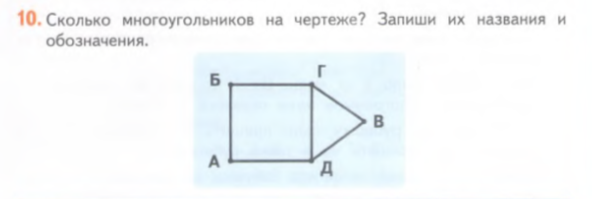
Рис. 6. Задача 10
В качестве творческой работы можно дать домашнее задание по составлению задач такого типа на листах А4. Составленные задачи дети могут презентовать перед классом, тем самым дети учатся выступать перед одноклассниками. Индивидуальные задания позволяют реализовывать не только предметные результаты, а также метапредметные и личностные.
Данные учебные задания и критерии оценивания учитель самостоятельно сможет проектировать в зависимости от целей и контроля обучения.
Во многих регионах Российской Федерации не хватает учителей, которые могут качественно преподавать математику, учитывая, развивая и формируя учебные и жизненные интересы различных групп обучающихся [1]. Поэтому проектирование учебных задач является важным профессиональным умением учителя, т. к. позволяет учителю составлять уровневые задания, в том числе олимпиадные задания.
Литература:
- Анисимова Т. И. Подготовка обучающихся к участию в математических олимпиадах / Т. И. Анисимова, А. Р. Ганеева // Педагогика и психология: актуальные вопросы теории и практики: материалы VIII Междунар. науч.–практ. конф. (Чебоксары, 23 окт. 2016 г.). — Чебоксары: ЦНС «Интерактив плюс», 2016. — № 3 (8). URL: https://interactive-plus.ru/article/114043/discussion_platform.
- Ганеева А. Р. Проектирование учебных заданий по математике на основе таксономии Блума / А. Р. Ганеева, П. Е. Шевелева //Проблемы и перспективы информатизации физико-математического образования: Материалы Всероссийской заочной научно-практической конференции, г. Елабуга, 14 ноября 2016 г., ред. кол. Ф. М. Сабирова (отв. ред.) и др. — Елабуга: Изд-во ЕИ КФУ, 2016. — С. 280–282
- Гончарова М. А. Образовательные технологии в школьном обучении математике. — Ростов н/Д: Феникс, 2014. — 264 с.
- Бойкина М. В. Контроль и оценка результатов обучения в начальной школе: Методические рекомендации / М. В. Бойкина, Ю. И. Глаголева. — Санкт-Петербург: КАРО, 2016. — 128 с.: ил. — (Петербургский вектор внедрения ФГОС НОО).







