В данной работе в явном виде найдены зависимости периода одномерного финитного движения релятивистской частицы от ее полной механической энергии во внешних симметричных потенциальных полях. Также получены точные выражения для зависимостей периода от амплитуды колебаний частицы в таких полях, для энергетических зависимостей периода движения частицы в ультрарелятивистском случае, а также приведено сравнение полученных результатов с вычисленными периодами финитного движения нерелятивистской частицы в рассматриваемых полях.
Ключевые слова: релятивистская частица, финитное движение, зависимость периода от энергии, зависимость периода от амплитуды, ультрарелятивистский случай
Рассматривая в рамках классической механики одномерное финитное движение частицы во внешнем потенциальном поле [1], можно для целого ряда полей точно решить задачу о нахождении периода движения частицы в этих полях и выяснить, как период зависит от полной энергии или амплитуды колебаний частицы. Кроме этого, в некоторых частных случаях можно точно решить и обратную задачу — задачу о нахождении заранее неизвестной потенциальной энергии классической частицы, совершающей финитное движение в некотором — зачастую достаточно сложном — поле, по известной зависимости периода (или частоты) такого движения от полной механической энергии частицы [2, 3] или от ее амплитуды колебаний [4].
Переход от классической механики к релятивистской при описании движения всегда приводит к появлению определенных релятивистских эффектов и более сложных зависимостей между исследуемыми величинами. В данной работе выясним, для каких потенциальных полей прямая задача о нахождении зависимости периода финитного движения частицы от ее полной энергии имеет точное и простое решение, если частица будет двигаться со скоростью, близкой к скорости света, и соответственно найдем энергетические и амплитудные зависимости периода движения релятивистской частицы в таких полях.
Итак, рассмотрим релятивистскую частицу массой покоя ![]() , которая может совершать одномерное финитное движение во внешнем поле с потенциальной энергией
, которая может совершать одномерное финитное движение во внешнем поле с потенциальной энергией ![]() , зависящей от координаты частицы. Будем предполагать, что
, зависящей от координаты частицы. Будем предполагать, что ![]() — монотонно возрастающая при
— монотонно возрастающая при ![]() функция, график которой симметричен относительно оси ординат, причем
функция, график которой симметричен относительно оси ординат, причем ![]() . Будем также считать внешнее поле стационарным, поэтому сохраняется полная энергия
. Будем также считать внешнее поле стационарным, поэтому сохраняется полная энергия ![]() релятивистской частицы в данном поле, которую можно представить в следующем виде [5]
релятивистской частицы в данном поле, которую можно представить в следующем виде [5]
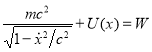 ,
,
где первое слагаемое — это энергия движения свободной релятивистской частицы, ![]() — ее скорость,
— ее скорость, ![]() — скорость света в вакууме.
— скорость света в вакууме.
Проинтегрируем это уравнение, разделяя переменные, в результате получим выражение, связывающее период финитного движения ![]() и потенциальную энергию
и потенциальную энергию ![]() релятивистской частицы в виде
релятивистской частицы в виде
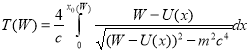 , (1)
, (1)
где
Как показал анализ интеграла в (1), в общем случае для произвольной (например, степенной с любым показателем) зависимости потенциальной энергии от координаты частицы, данный интеграл не вычисляется точно, однако можно рассмотреть решение поставленной задачи в двух следующих частных случаях.
Пусть релятивистская частица совершает финитное движение в симметричном поле с потенциальной энергией ![]() при
при ![]() и
и ![]() при
при ![]() , где положительный коэффициент
, где положительный коэффициент ![]() численно равен возвращающей силе внешнего поля, действующей на частицу. Тогда, вычисляя интеграл в (1) с данным полем, получим точную зависимость периода финитного движения релятивистской частицы от ее полной энергии в следующем виде
численно равен возвращающей силе внешнего поля, действующей на частицу. Тогда, вычисляя интеграл в (1) с данным полем, получим точную зависимость периода финитного движения релятивистской частицы от ее полной энергии в следующем виде
![]() . (2)
. (2)
Отметим несколько следствий из формулы (2). Во-первых, в случае энергий релятивистской частицы, много больших ее энергии покоя (![]() ), т. е. в так называемом ультрарелятивистском случае [6], получаем, что период финитного движения частицы линейным образом зависит от полной энергии частицы:
), т. е. в так называемом ультрарелятивистском случае [6], получаем, что период финитного движения частицы линейным образом зависит от полной энергии частицы:
![]() .
.
Во-вторых, для рассматриваемого поля легко получить приближение формулы (2) в нерелятивистском случае (при ![]() ) в виде
) в виде
![]() , (3)
, (3)
где ![]() — полная энергия нерелятивистской частицы. Заметим, что непосредственное вычисление периода финитного движения частицы в исследуемом поле в нерелятивистском случае (как это, например, описано в [1]) приводит к тому же результату (3).
— полная энергия нерелятивистской частицы. Заметим, что непосредственное вычисление периода финитного движения частицы в исследуемом поле в нерелятивистском случае (как это, например, описано в [1]) приводит к тому же результату (3).
Наконец, в-третьих, используя условие ![]() , где
, где ![]() — амплитуда колебаний частицы во внешнем поле
— амплитуда колебаний частицы во внешнем поле ![]() , из (2) получаем точное выражение для зависимости периода финитного движения релятивистской частицы от ее амплитуды в виде
, из (2) получаем точное выражение для зависимости периода финитного движения релятивистской частицы от ее амплитуды в виде
![]() ,
,
где
Далее рассмотрим еще один частный случай, при котором возможно точное вычисление интеграла (1), а именно приведем полученное окончательное выражение для энергетической зависимости периода финитного движения релятивистской частицы в симметричном поле ![]() (
(![]() — постоянное положительное число):
— постоянное положительное число):
![]() . (4)
. (4)
Аналогично первому случаю получим несколько следствий из формулы (4). Во-первых, в ультрарелятивистском случае (![]() ) следует квадратичная зависимость периода от полной энергии частицы:
) следует квадратичная зависимость периода от полной энергии частицы:
![]() .
.
Во-вторых, для рассматриваемого поля также нетрудно получить приближение формулы (4) в нерелятивистском случае в виде
![]() , (5)
, (5)
где ![]() — полная энергия нерелятивистской частицы в данном поле. Также отметим, что выражение (5) тоже совпадает с энергетической зависимостью периода финитного движения частицы в исследуемом поле, получаемой в рамках классической механики [1].
— полная энергия нерелятивистской частицы в данном поле. Также отметим, что выражение (5) тоже совпадает с энергетической зависимостью периода финитного движения частицы в исследуемом поле, получаемой в рамках классической механики [1].
И, наконец, в-третьих, с учетом условия ![]() , из (4) получим точное выражение для зависимости периода финитного движения релятивистской частицы во внешнем поле
, из (4) получим точное выражение для зависимости периода финитного движения релятивистской частицы во внешнем поле ![]() от ее амплитуды
от ее амплитуды ![]() в следующем виде
в следующем виде
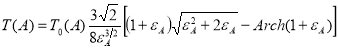 , (6)
, (6)
где теперь ![]() — период финитного движения нерелятивистской частицы в поле
— период финитного движения нерелятивистской частицы в поле ![]() , который можно получить из формулы (5), а также для краткости записи здесь введено обозначение
, который можно получить из формулы (5), а также для краткости записи здесь введено обозначение ![]() . Легко проверить, что в случае малого
. Легко проверить, что в случае малого ![]() в первом приближении период (6) принимает вид классической зависимости
в первом приближении период (6) принимает вид классической зависимости ![]() в данном поле.
в данном поле.
Таким образом, расчет и анализ периода финитного движения релятивистской частицы в двух данных симметричных потенциальных полях показал, что он существенно отличается от периода финитного движения нерелятивистской частицы в тех же самых полях. В силу релятивистских эффектов усложняется зависимость периода как от полной энергии релятивистской частицы, так и от амплитуды ее колебаний по сравнению с результатами, получаемыми в рамках классической механики.
Литература:
1. Ландау Л. Д., Лифшиц Е. М. Теоретическая механика. Т.1. Механика. — М., 2004. — 224 с.
2. Кочкин С. А., Островский В. В. Определение потенциальной энергии частицы по известной линейной энергетической зависимости периода ее финитного движения в потенциальной яме // Молодой ученый. — 2016. — № 18(122). — С. 20–22.
3. Кочкин С. А., Розевика А. А. Задача о нахождении потенциальной энергии классической частицы по известной степенной зависимости периода ее финитного движения от полной энергии // Актуальные проблемы гуманитарных и естественных наук. — 2016. — № 8(1). — С. 23–26.
4. Кочкин С. А., Бригинец С. А. О нахождении потенциальной энергии классической частицы во внешнем поле по известной степенной амплитудной зависимости ее периода колебаний // Проблемы современной науки и образования. — 2016. — № 18(60). — С. 6–8.
5. Истеков К. К. Курс теоретической физики. — А., 2005. — 574 с.
6. Сивухин Д. В. Общий курс физики. Т. 1. Механика. — М., 2005. — 560 с.







