Определение продолжительности сушки травы в полевых условиях облегчает прогнозирование технологического процесса производства кормов из трав и обеспечивает оперативное управление им непосредственно в процессе его реализации, что способствует получению для животных кормов высокого качества. Применение экспоненциальных уравнений расчета продолжительности сушки травы затруднено, ввиду сложности в определении эмпирического коэффициента. Данный коэффициент экспоненты учитывает интенсивность испарения влаги из травы, погодные условия, вид травы, фазы вегетации и другие факторы. Для его расчёта по экспериментальным данным применены вычислительные средства, и соответствующее программное обеспечение. Рассмотрены два метода решения нелинейного алгебраического уравнения (итерационный и поиск параметра) с использованием компьютерных систем «MathCAD» и «Microsoft Excel». Разница расчетов значений равномерной влажности составила 3,34 %, а эмпирического коэффициента — 3,96 %.
Ключевые слова: корма, сушка травы, уравнения, методы решения, компьютерные системы
Процесс сушки (провяливания) травы в полевых условиях при заготовке кормов из трав является самым продолжительным по времени, на протекание которого влияет огромное количество факторов стохастического характера [1]. От качества его реализации в целом зависит энергетическая и питательная ценность полученных кормов. В процессе сушки травы в полевых условиях выполняются операции ворошения, оборачивания и сгребания в валки с целью ускорения испарения влаги из скошенной травы для обеспечения её консервации с минимумом потерь энергетической ценности. В связи с чем, требуется контроль влажности провяливаемой массы для принятия рациональных технико-технологического решения в процессе заготовки кормов из трав [2] с учётом складывающихся погодных условий, фазы вегетации травы, её ботанического состава и др. условий.
На Северо-Западе России провяливание травы, как правило, производится в полевых условиях в прокосе, так как в данном случае процесс испарения влаги происходит более интенсивно, чем в валках.
Уравнение сушки травы имеет вид [3]:
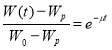 ,(1)
,(1)
где ![]() — начальная влажность травы, %;
— начальная влажность травы, %;
![]() — текущая по времени влажность провяливаемой травы, %;
— текущая по времени влажность провяливаемой травы, %;
![]() — равновесная влажность травы, %;
— равновесная влажность травы, %;
![]() — время сушки, ч.;
— время сушки, ч.;
На основе уравнения (1) определяется длительность выполнения операции провяливания травы [4], однако для оперативного использования уравнения имеются трудности по определению его коэффициентов. Значения ![]() и
и ![]() могут быть измерены влагомером. Коэффициенты
могут быть измерены влагомером. Коэффициенты ![]() и
и ![]() ранее определялись расчетом при обработке некоторого объема экспериментальных данных [5]. Коэффициент
ранее определялись расчетом при обработке некоторого объема экспериментальных данных [5]. Коэффициент ![]() может быть так же определен по i-d диаграмме при известной температуре и влажности воздуха. По известному значению
может быть так же определен по i-d диаграмме при известной температуре и влажности воздуха. По известному значению ![]() коэффициент сушки
коэффициент сушки ![]() определяется по формуле (2) Лыкова А. В. [3]:
определяется по формуле (2) Лыкова А. В. [3]:
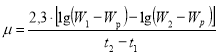 .(2)
.(2)
Коэффициенты ![]() и
и ![]() можно определять более просто и оперативно, используя современные мобильные вычислительные средства (ноутбуки, планшеты и т. п.) и соответствующее программное обеспечение.
можно определять более просто и оперативно, используя современные мобильные вычислительные средства (ноутбуки, планшеты и т. п.) и соответствующее программное обеспечение.
Для определения коэффициентов необходимо выполнить измерение влажности провяливаемой травы при двух значениях временного интервала: ![]() и
и ![]() , т. е.
, т. е. ![]() и
и ![]() . Для определения коэффициентов
. Для определения коэффициентов ![]() и
и ![]() , прологарифмируем уравнение (1):
, прологарифмируем уравнение (1):
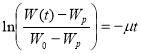 .(3)
.(3)
Подставим в уравнение (3) ![]() и
и ![]() , и представим полученные уравнения в следующем виде:
, и представим полученные уравнения в следующем виде:
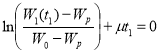 ;(4)
;(4)
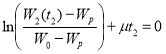 .(5)
.(5)
Уравнения (4) и (5) представляют собой систему нелинейных алгебраических уравнений, и решается итерационным методом с помощью математического пакета «MathCAD» [6]. На рисунке 1 представлен расчет коэффициентов ![]() и
и ![]() . Для расчетов задаются значения, например,
. Для расчетов задаются значения, например, ![]() %,
%, ![]() %,
%, ![]() %,
%, ![]() ч.,
ч., ![]() ч. Введены обозначения:
ч. Введены обозначения: ![]() и
и ![]() . Решение выполняется операторами программы «Given» и «Find» [6]. Решение выдается программой в матричном виде:
. Решение выполняется операторами программы «Given» и «Find» [6]. Решение выдается программой в матричном виде: ![]() % и
% и ![]() .
.
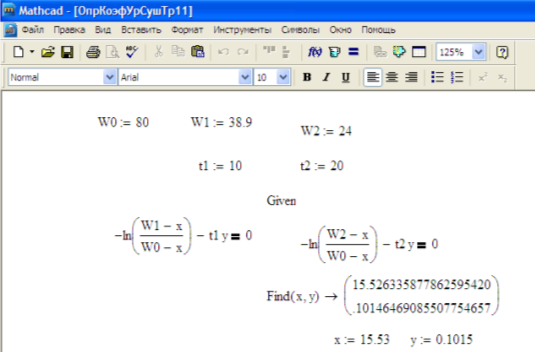
Рис. 1. Программа в системе MathCAD для определения коэффициентов
Определение коэффициентов можно выполнить так же и в системе «Microsoft Office Excel» через «Поиск параметра» [7].
Решим уравнения (4) и (5) относительно ![]() и приравняем их, умножив на
и приравняем их, умножив на![]() :
:
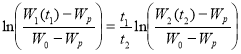 .(6)
.(6)
Из уравнения (6) необходимо определить равновесную влажность ![]() .
.
Введем следующие обозначения:
![]() ,
, 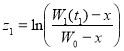 ,
, 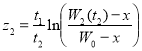 .(7)
.(7)
Запишем следующее уравнение:
![]() .(8)
.(8)
Решение уравнения (8) дает значение ![]() , и его можно получить методом поиска.
, и его можно получить методом поиска.
Более наглядно решение получается графическим методом, путем построения кривой ![]() , решение получается при пересечении функцией
, решение получается при пересечении функцией ![]() оси абсцисс. Расчет
оси абсцисс. Расчет ![]() необходимо выполнить для некоторого множества
необходимо выполнить для некоторого множества ![]() , внутри которого должно быть искомое решение.
, внутри которого должно быть искомое решение.
Для нашего случая выбран массив
Программа «Microsoft Excel»рассчитывает ![]() ,
, ![]() ,
, ![]() и строит график
и строит график ![]() . Если
. Если ![]() не пересекает ось абсцисс, то необходимо изменить интервал значений «
не пересекает ось абсцисс, то необходимо изменить интервал значений «![]() ».
».
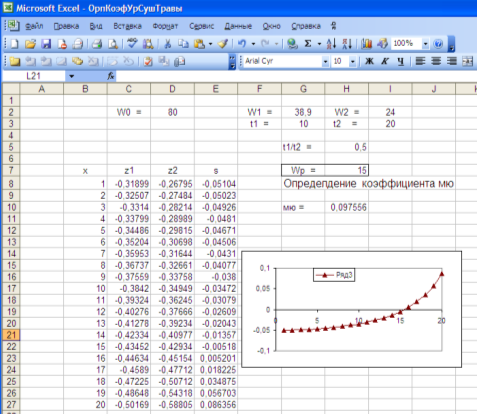
Рис. 2. Программа в системы Excel для определения коэффициентов ![]() и
и ![]()
Как видно из рисунка 2, кривая ![]() пересекает ось абсцисс при
пересекает ось абсцисс при ![]() , т. е.
, т. е. ![]() %. Значение
%. Значение ![]() рассчитано по формуле (2) и составляет
рассчитано по формуле (2) и составляет ![]() .
.
Результаты расчетов ![]() и
и ![]() в компьютерной системе «MathCAD» и в программном приложении «Microsoft Excel» совпадают достаточно близко, и таким образом разность значений составляет для равномерной влажности 3,34 %, а эмпирического коэффициента уравнения сушки — 3,96 %.
в компьютерной системе «MathCAD» и в программном приложении «Microsoft Excel» совпадают достаточно близко, и таким образом разность значений составляет для равномерной влажности 3,34 %, а эмпирического коэффициента уравнения сушки — 3,96 %.
Выявленные эмпирические коэффициенты позволяют рассчитать по уравнению сушки травы динамику изменения влажности травы после скашивания в зависимости от погодных условий, фазы вегетации травы, ботанического состава травостоя и других факторов. Зная скорость влагоотдачи, осуществляется прогнозирование продолжительности времени сушки травы в поле, на основании чего предоставляется возможность осуществлять оперативное управление технологическим процессом заготовки кормов из трав, что существенно способствует получению кормов из трав различного вида и высокого качества для животных.
Литература:
- Попов В. Д., Сухопаров А. И. Информационная и структурная модели управления технологиями в растениеводстве // Вестник РАСХН. — 2010. — № 3. — С. 7–8.
- Сухопаров А. И. Условия и показатели управления технологиями заготовки кормов из трав и зерна // Технологии и технические средства механизированного производства продукции растениеводства и животноводства: Сб. науч. тр. Вып. 82. — С-Пб.: ГНУ СЗНИИМЭСХ Россельхозакадемии, 2010. — С. 17–24.
- Лыков А. В. Теория сушки. — М.: Энергия, 1968. — 472 с.
- Валге А. М. Динамика сушки травы в полевых условиях // Технология и технические средства механизированного производства продукции растениеводства и животноводства в Нечерноземной зоне России. Сб. науч. тр. Вып. 65. — С-Пб.: НИПТИМЭСХ НЗ, 1995. — С. 43–49.
- Зубрилин А. А. Научные основы консервирования зеленых кормов. — М.: ОГИЗ СельхозГИЗ, 1946. — 368 с.
- Кирьянов Д. В. Самоучитель MathCAD 2001. — СПб.: БХВ-Петербург, 2001. — 544 с.
- Чекотовский Э. В. Графический анализ статистических данных в Microsoft Excel 2000. — М.: Вильямс, 2002. — 464 с.







