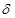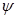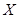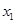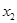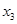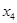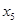В настоящее время наблюдается бурный рост промышленности, развитие производства, и вместе с этим происходит все большее усложнение объектов управления. Это сопровождается уменьшением априорной информации о подобных объектах. Таким образом, связь между теорией управления и теорией идентификации становится все более тесной.
Идентификацией называется процесс решения задачи построения математических моделей, адекватно описывающих поведение реальной системы, по результатам наблюдений параметров этой системы.
Постановка задачи идентификации зависит от уровня имеющейся априорной информации.
Общая постановка задачи идентификации
Пусть имеется некоторый объект, описываемый уравнением
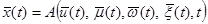 (1)
(1)
где 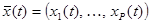 - выходной вектор,
- выходной вектор, 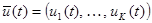 - вектор управляемых входных переменных,
- вектор управляемых входных переменных, 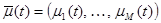 - вектор неуправляемых входных переменных,
- вектор неуправляемых входных переменных, 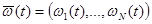 - вектор неконтролируемых входных переменных (об их существовании исследователь может и не знать),
- вектор неконтролируемых входных переменных (об их существовании исследователь может и не знать), 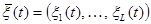 - случайные возмущения с нулевым математическим ожиданием и ограниченной дисперсией,
- случайные возмущения с нулевым математическим ожиданием и ограниченной дисперсией, 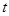 - время,
- время, 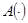 - неизвестный оператор, преобразующий входные переменные объекта в выходные.
- неизвестный оператор, преобразующий входные переменные объекта в выходные.
Графически данный объект можно представить в виде
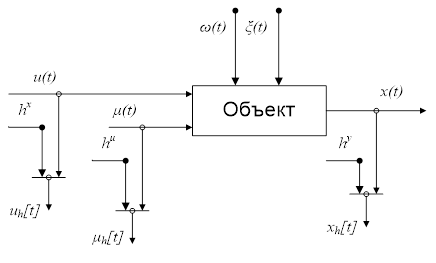
Рисунок 1. Общая схема наблюдения входных и выходных переменных объекта
На рисунке 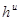 ,
, 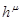 ,
, 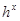 являются случайными величинами, представляющими собой ошибки измерения значений переменных
являются случайными величинами, представляющими собой ошибки измерения значений переменных 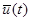 ,
, 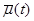 и
и 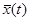 , причем
, причем 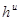 ,
, 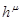 ,
, 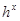 имеют нулевое математическое ожидание и ограниченную дисперсию;
имеют нулевое математическое ожидание и ограниченную дисперсию; 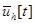 ,
, 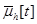 и
и 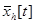 - измерения со случайными ошибками управляемых входных, неуправляемых входных и выходных переменных объекта в дискретные моменты времени.
- измерения со случайными ошибками управляемых входных, неуправляемых входных и выходных переменных объекта в дискретные моменты времени.
Ставится задача построения модели объекта (1) на основании выборки наблюдений 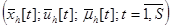 и при наличии некоторых дополнительных априорных сведений. Далее для простоты выборку будем обозначать как
и при наличии некоторых дополнительных априорных сведений. Далее для простоты выборку будем обозначать как 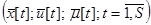 .
.
По мере усиления неопределенности задача идентификации может быть рассмотрена при следующих уровнях:
· байесов уровень априорной информации, при котором возможно как наличие полной информации об объекте (точно заданы модель объекта, статистические характеристики наблюдений и помех), так и наличие неполной информации (статистические характеристики наблюдений и помех, а также вид модели объекта заданы с точностью до набора параметров). Подробно этот случай исследовался в монографии А.А. Фельдбаума[3];
· параметрический уровень неопределенности, при котором известны структура модели объекта с точностью до набора параметров и некоторые характеристики помех, но законы распределения наблюдений и этих помех не известны;
· непараметрический уровень априорной информации, при котором не известны ни структура модели, ни законы распределения наблюдений и помех, а известны лишь некоторые качественные характеристики объекта (статический или динамический, однозначны или нет зависимости между переменными, является ли объект многомерным или нет). Решение задачи идентификации в этом случае производится при помощи методов непараметрической статистики[2].
В условиях байесова и параметрического уровней априорной информации решается задача идентификации в «узком» смысле. Она заключается в выборе каким-то образом параметрического класса операторов 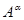 , например,
, например,
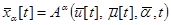 , (2)
, (2)
и в оценивании параметров 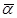 на основе имеющейся выборки. При этом существенное влияние на качество модели оказывает то, насколько точно выбрана структура объекта. Также оценка параметров может оказаться достаточно сложной из-за многомерности объекта, взаимосвязи переменных или влияния помех.
на основе имеющейся выборки. При этом существенное влияние на качество модели оказывает то, насколько точно выбрана структура объекта. Также оценка параметров может оказаться достаточно сложной из-за многомерности объекта, взаимосвязи переменных или влияния помех.
При решении задачи идентификации в «широком» смысле предполагается отсутствие этапа выбора параметрического класса операторов 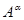 . Вместо этого, основываясь на качественных характеристиках объекта, производится оценка его структуры с помощью выборок наблюдений входных и выходных переменных. В условиях непараметрического уровня априорной информации решается именно задача идентификации в «широком» смысле.
. Вместо этого, основываясь на качественных характеристиках объекта, производится оценка его структуры с помощью выборок наблюдений входных и выходных переменных. В условиях непараметрического уровня априорной информации решается именно задача идентификации в «широком» смысле.
Параметрическая идентификация
При параметрической идентификации структура объекта, т.е. оператор 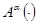 считается известным с точность до набора параметров (в общем случае он выбирается из класса операторов, который определяется на основании имеющейся априорной информации). Причем, из-за того, что неконтролируемые переменные
считается известным с точность до набора параметров (в общем случае он выбирается из класса операторов, который определяется на основании имеющейся априорной информации). Причем, из-за того, что неконтролируемые переменные 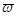 нельзя измерить, а, следовательно, и использовать в оценке, то оператор
нельзя измерить, а, следовательно, и использовать в оценке, то оператор 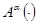 никогда не совпадает с оператором
никогда не совпадает с оператором 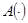 . При этом модель искомого объекта (1) представляется в виде (2).
. При этом модель искомого объекта (1) представляется в виде (2).
В этом случае необходимо на основании имеющейся выборки 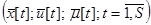 определить такие параметры
определить такие параметры 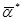 , при которых будет достигаться минимум заданного критерия оптимальности. Таким образом, задача параметрической идентификации сводится к задаче оптимизации этого критерия по неизвестным параметрам.
, при которых будет достигаться минимум заданного критерия оптимальности. Таким образом, задача параметрической идентификации сводится к задаче оптимизации этого критерия по неизвестным параметрам.
В общем случае критерий оптимизации выбирается в виде математического ожидания от вектор-функции, аргументом которой является разность между выходом полученной модели и выходом рассматриваемого объекта
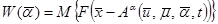 .
.
Причем, этот функционал неизвестен, из-за того, что нам не известны плотности распределения случайных величин, по которым производится усреднение.
Оценивание параметров в моделях осуществляется с помощью различных итеративных вероятностных процедур, например, с помощью процедуры Кифера-Вольфовица, которая записывается в виде
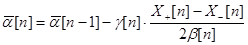
где
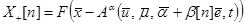 ;
;
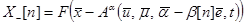 ;
;
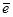 - единичный орт-вектор;
- единичный орт-вектор;
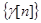 и
и 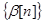 - некоторые числовые последовательности, удовлетворяющие условиям
- некоторые числовые последовательности, удовлетворяющие условиям
1) 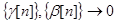 ; 2)
; 2) 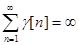 ;
;
3) 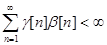 ; 4)
; 4)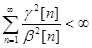 .
.
Из накладываемых условий обычно следует, что в среднем значение 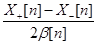 совпадает со значением градиента
совпадает со значением градиента 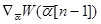 в точке
в точке 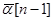 . Причем, при выполнении этих условий для произвольного
. Причем, при выполнении этих условий для произвольного 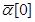 имеет место
имеет место 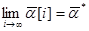 .
.
Непараметрическая идентификация
В случае непараметрической идентификации дополнительно требуются сведения об однозначности зависимостей между входными и выходными переменными.
Если зависимости являются однозначным, то в качестве оценки оператора 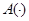 берется усредненная зависимость между входными и выходными переменными – регрессия, что вполне целесообразно из-за наличия помех.
берется усредненная зависимость между входными и выходными переменными – регрессия, что вполне целесообразно из-за наличия помех.
Регрессия, как известно, представляет собой условное математическое ожидание
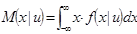 (3)
(3)
где 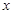 - выходная переменная,
- выходная переменная, 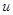 - входная переменная,
- входная переменная, 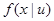 - условная плотность распределения вероятности.
- условная плотность распределения вероятности.
Так как условная плотность распределения вероятности неизвестна, то строится непараметрическая оценка регрессии.
Данную плотность распределения можно расписать как
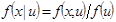 .
.
Непараметрические оценки плотности 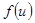 и совместной плотности распределения
и совместной плотности распределения 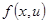 имеют вид[4]
имеют вид[4]
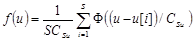
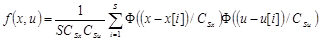
Тогда оценка условной плотности представляет собой
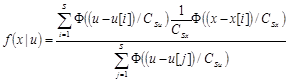 .
.
Известно, что выражение 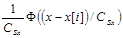 в пределе представляет собой дельта-функцию
в пределе представляет собой дельта-функцию 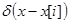 , которая обладает следующим важным свойством [4]
, которая обладает следующим важным свойством [4]
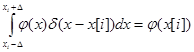 (4)
(4)
где 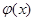 - некоторая функция.
- некоторая функция.
Подставим полученную оценку условной плотности распределения вероятности в формулу (3)
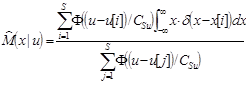
и воспользуемся свойством (4), в итоге имеем
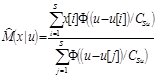 .
.
В многомерном случае оценка имеет вид
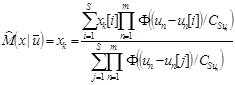 .
.
Ядерная функция 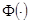 и параметры размытости
и параметры размытости 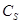 обладают следующими свойствами [2]:
обладают следующими свойствами [2]:
1) 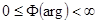 ; 2)
; 2) 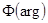 =
=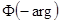 ;
;
3) 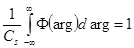 ; 4)
; 4) 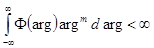 , при m>0;
, при m>0;
5) 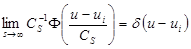 ; 6)
; 6) 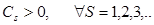
Регрессия представляет собой некоторую усредненную зависимость. Поэтому получаемая оценка регрессии обладает сглаживающим свойством, причем степень сглаживания напрямую зависит от численного значения параметра размытости.
Выбор параметра размытости
В общем случае задача выбора параметра размытости сводится к задаче минимизации некоторого критерия оптимальности, характеризующего правильность построенной оценки.
Наиболее часто в качестве критерия выбирается среднеквадратическая ошибка между выходом объекта и выходом модели
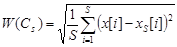 .
.
Также предлагается использовать так называемый “скользящий экзамен”, когда имеющаяся выборка своеобразно разбивается на обучающую и экзаменующую. В каждой точке выборки оценка строится без учета этой точки, при этом, выбором величины параметра размытости задается сколько соседних точек будет образовывать оценку. А качество оценки проверяется в текущей точке. Таким образом, параметр размытости не может быть меньше такого значения, при котором в область захвата колоколообразной функции не попадет ни одной соседней к текущей точки. За счет этого при настройке параметра размытости методом “скользящего экзамена” всегда наблюдается сглаживающий эффект.
Минимизацию критерия можно проводить любым из известных методов оптимизации, например, методом покоординатного спуска или методом деформируемого многогранника Нелдера – Мида [4].
Комбинированные модели
На практике довольно часто встречается случай, когда объем априорной информации не соответствует ни одному из приведенных выше, а именно, когда зависимости между некоторыми переменными многосвязного объекта известны полностью или с точностью до набора параметров, а остальные не известны, т.е. имеет место сочетание нескольких уровней априорной информации. Такие ситуации возникают, например, при построении моделей производственных комплексов (например, предприятия металлургической промышленности), когда часть связей может быть параметризована (например, на основе физико-химических закономерностей), часть известна точно, а часть связей неизвестна, но заданы некоторые качественные характеристики. Подобные объекты зачастую состоят из более мелких локальных объектов (далее ЛО), причем выходные переменные некоторых ЛО являются входами для других. Это приводит к тому, что описание объектов представляется не в традиционной форме «вход – оператор связи – выход», а неявно в виде некоторой системы уравнений.
Объекты, описание которых представляет собой некоторую систему неявных функций от их входных и выходных переменных, называются многосвязными.
Модели, построенные в таких условиях, называются комбинированными.
Рассматриваются многосвязные объекты, состоящие из 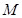 локальных объектов. Обозначим входные переменные как
локальных объектов. Обозначим входные переменные как 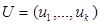 , а выходные как
, а выходные как 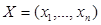 , причем
, причем 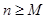 , т.е. некоторые ЛО могут иметь более одной выходной переменной. К тому же U включают в себя как управляемые
, т.е. некоторые ЛО могут иметь более одной выходной переменной. К тому же U включают в себя как управляемые 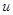 так и неуправляемые
так и неуправляемые 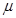 входные переменные объекта.
входные переменные объекта.
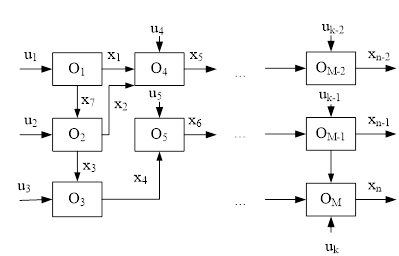
Рисунок 2. Пример многосвязной системы.
Локальные объекты имеют различные уровни априорной информации: байесов, параметрический и непараметрический. Имеется выборка наблюдений входных и выходных переменных 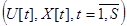 . Необходимо построить модель объекта.
. Необходимо построить модель объекта.
В общем случае задача построения комбинированной модели решается в два этапа. На первом этапе строится система уравнений, описывающая объект, а на втором этапе эта система решается при фиксированных значениях входных переменных для получения прогноза выхода [1].
Подобная двухуровневая структура обусловлена тем, что ЛО, из которых состоят искомые объекты, являются взаимосвязанными, т.е. они каким-то образом влияют друг на друга, выходы одних ЛО являются входами для других, таким образом, модель всего объекта представляет собой систему неявных уравнений, представляющую собой набор моделей каждого ЛО. Поэтому, чтобы получить выход модели и оценить ее качество (оптимальность в смысле какого-либо критерия), необходимо решить эту систему при фиксированных значениях входных переменных.
Общий вид системы уравнений:
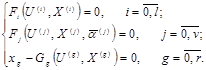 (5),
(5),
где l- число ЛО с байесовым уровнем априорной информации; v- число ЛО с параметрическим уровнем априорной информации; r- число ЛО с непараметрическим уровнем априорной информации; 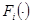 - известные функции;
- известные функции; 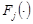 - функции, известные с точностью до набора параметров
- функции, известные с точностью до набора параметров 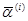 ; запись
; запись 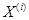 означает набор компонент вектора
означает набор компонент вектора 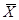 , входящих в i-тое уравнение;
, входящих в i-тое уравнение; 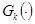 - непараметрические статистики
- непараметрические статистики
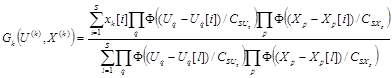 , где q- номера U, входящих в j-е уравнение, p- номера X, входящих в j-е уравнение. Ядерные функции
, где q- номера U, входящих в j-е уравнение, p- номера X, входящих в j-е уравнение. Ядерные функции 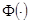 и параметры размытости
и параметры размытости 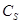 удовлетворяют условиям, рассмотренным выше.
удовлетворяют условиям, рассмотренным выше.
При построении системы уравнений производится обучение параметрических и непараметрических моделей ЛО.
На втором этапе построения модели производится решение полученной системы при фиксированном входном воздействии в какой-либо требуемой точке 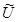 .
.
Решением системы уравнений (5) являются такие значения вектора 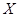 , при которых левые и правые части каждого уравнения в системе превращаются в тождество. Это означает, что в каждой оценке выходных переменных ЛО необходимо учесть все имеющиеся уравнения. А именно, оценки решений должны искаться при условии равенства нулю левых частей каждого из уравнений в системе.
, при которых левые и правые части каждого уравнения в системе превращаются в тождество. Это означает, что в каждой оценке выходных переменных ЛО необходимо учесть все имеющиеся уравнения. А именно, оценки решений должны искаться при условии равенства нулю левых частей каждого из уравнений в системе.
Чтобы решить полученную систему уравнений, необходимо сгенерировать выборку вспомогательных переменных 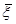 , которые, по сути, являются невязками между выходами объекта и модели при фиксированном входном воздействии и представляют собой левые части уравнений в системе
, которые, по сути, являются невязками между выходами объекта и модели при фиксированном входном воздействии и представляют собой левые части уравнений в системе
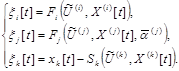 (6) ,
(6) ,
где t=1,..,S.
В точках решений эти невязки должны быть равны нулю, но так как присутствуют случайные величины в виде помех, то решение системы (5) будем искать как условное математическое ожидание вида 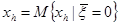 , где h=1,..,n. Оператор математического ожидания заменим на его непараметрическую оценку
, где h=1,..,n. Оператор математического ожидания заменим на его непараметрическую оценку
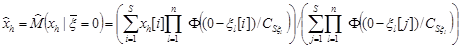 (7)
(7)
Параметры размытости 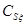 , соответствующие невязкам, настраиваются путем генерации матрицы невязок
, соответствующие невязкам, настраиваются путем генерации матрицы невязок
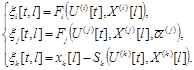
где 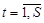 ,
, 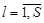 и последующей минимизацией обобщенного критерия
и последующей минимизацией обобщенного критерия
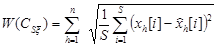 .
.
Особый интерес представляет случай, когда система (5) имеет более одного решения. Несколько корней в таких системах означает, что при фиксированном входном воздействии некоторые компоненты выходного вектора принимают несколько различных значений. В такой ситуации невязки будут близки к нулю при нескольких значениях выходных переменных. Особенность оценки (7) заключается в том, что в случае, когда при одном значении входного воздействия имеется несколько значений выходной переменной, то в качестве оценки выхода будет выступать не одно из значений выходной переменной, а некоторая средняя величина, при этом отклонение от истинного выхода объекта будет значительным.
Был предложен следующий итерационный алгоритм поиска решений системы (5).
1. Выбирается начальное приближение 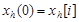 , где i соответствует такому значению невязок, что
, где i соответствует такому значению невязок, что
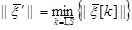 (8),
(8),
где 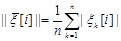 .
.
2. Осуществляется итерационный процесс поиска корня системы по формуле
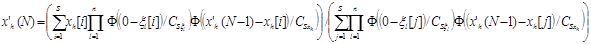 где N=1,2,.., пока выполняется условие
где N=1,2,.., пока выполняется условие 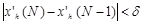 ,
, 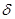 - заданное число.
- заданное число.
3. Производится переход к шагу 1, причем начальная точка выбирается по формуле (8), но минимум ищется по всей выборке, исключая использованную на предыдущей итерации точку.
Поиск корней системы заканчивается, если в формуле (8) станет выполняться условие 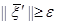 , где
, где 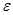 - некоторое заданное число.
- некоторое заданное число.
В итоге после k- раз использования алгоритма получается k решений системы 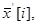 i=1,..,k. Возможна ситуация, когда на нескольких итерациях будет найден один и тот же корень системы, поэтому предлагается проверять полученные решения на близость по каждой координате в соответствии с формулой
i=1,..,k. Возможна ситуация, когда на нескольких итерациях будет найден один и тот же корень системы, поэтому предлагается проверять полученные решения на близость по каждой координате в соответствии с формулой 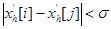 , где i=1,..,k, j=1,..,k,
, где i=1,..,k, j=1,..,k, 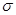 - некоторое заданное число. Таким образом, образуется
- некоторое заданное число. Таким образом, образуется 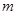 групп решений системы. Решения, находящиеся в одной группе считаются эквивалентными. Чтобы получить m решений системы, предлагается искать среднее арифметическое значение решений в каждой группе.
групп решений системы. Решения, находящиеся в одной группе считаются эквивалентными. Чтобы получить m решений системы, предлагается искать среднее арифметическое значение решений в каждой группе.
Результаты исследований
Методом статистического моделирования было осуществлено исследование работоспособности рассмотренного выше итерационного алгоритма поиска решений.
В качестве исходного объекта была выбрана система пяти нелинейных уравнений
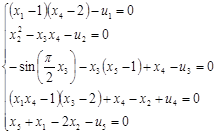
Система была подобрана специальным образом, и при значении входного вектора 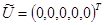 эта система имеет два решения
эта система имеет два решения 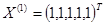 и
и 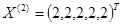 .
.
Первые два уравнения считались известными, а последние три – заданы выборками наблюдений (непараметрический уровень).
Комбинированная модель имела вид
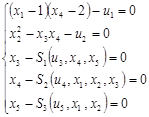
где непараметрические статистики 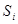 записываются в виде
записываются в виде
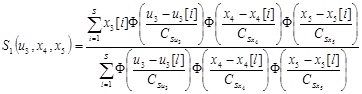 ,
,
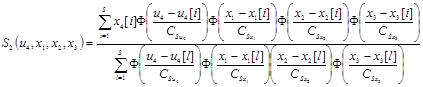 ,
,
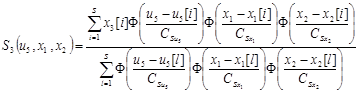 .
.
Параметры размытости в этих оценках настраивались с помощью “скользящего экзамена”, при этом критерий минимизировался методом деформируемого многогранника Нелдера-Мида.
Для настройки параметров размытости, соответствующим невязкам последовательно в качестве входного воздействия задавалось каждое значение входного вектора из обучающей выборки, строились матрицы невязок и минимизировался критерий, рассмотренный выше.
Целью было проверить работоспособность алгоритма в случае нескольких корней, поэтому система решалась в точке 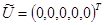 .
.
Используя рассмотренный выше итерационный алгоритм, был осуществлен поиск решений системы при различных значениях параметров.
Объем обучающей выборки 100. Помехи отсутствуют.
|
Параметр |
|
|
|
|
||||||
|
Значение |
0.000001 |
1 |
0.01 |
0.1 |
||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
4 |
|
|||
|
2 |
2 |
2 |
2 |
2 |
2 |
4 |
|
|||
|
Параметр |
|
|
|
|
||||||
|
Значение |
0.000001 |
1 |
0.1 |
0.1 |
||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
12 |
|
|||
|
2 |
2 |
2 |
2 |
2 |
2 |
12 |
|
|||
|
Параметр |
|
|
|
|
||||||
|
Значение |
0.000001 |
1 |
0.001 |
0.1 |
||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
1 |
1 |
1 |
1 |
1 |
1 |
2 |
|
|||
|
2 |
2 |
2 |
2 |
2 |
2 |
2 |
|
|||
|
Параметр |
|
|
|
|
||||||
|
Значение |
0.000001 |
1 |
0.0001 |
0.1 |
||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
1 |
2 |
2 |
2 |
2 |
2 |
1 |
|
|||
|
2 |
2 |
2 |
2 |
2 |
2 |
1 |
|
|||
При увеличении параметра 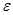 , соответствующего условию окончания поиска корней системы, наблюдалось увеличение итераций поиска, при этом найденные корни системы совпадали с истинными. При уменьшении этого параметра наблюдалось снижение числа итераций, но при слишком маленьком значении параметра не все корни были найдены. Влияние остальных параметров было незначительно.
, соответствующего условию окончания поиска корней системы, наблюдалось увеличение итераций поиска, при этом найденные корни системы совпадали с истинными. При уменьшении этого параметра наблюдалось снижение числа итераций, но при слишком маленьком значении параметра не все корни были найдены. Влияние остальных параметров было незначительно.
Вводилась помеха таким образом, что к входным и выходным переменным добавлялись небольшие случайные числа с равномерным законом распределения. При этом вновь производилось обучение.
|
Параметр |
|
|
|
|
|||||||||||||
|
Значение |
0.000001 |
1 |
0.01 |
0.1 |
|||||||||||||
|
Помеха 1% |
|
||||||||||||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
1 |
0.9956 |
0.9907 |
1.0003 |
1.0086 |
1.0042 |
4 |
|
||||||||||
|
2 |
1.9878 |
2.0152 |
2.011 |
2.0102 |
2.0022 |
4 |
|
||||||||||
|
Помеха 5% |
|
||||||||||||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
||||||||||||||
|
|
|
|
|
|
|
||||||||||||
|
1 |
1.006 |
0.9882 |
1 |
1.0055 |
0.9846 |
2 |
|
||||||||||
|
2 |
1.9851 |
1.9765 |
1.9108 |
1.9629 |
1.9368 |
2 |
|
||||||||||
|
Параметр |
|
|
|
|
||||||
|
Значение |
0.000001 |
2 |
0.01 |
0.1 |
||||||
|
Помеха 5% |
|
|||||||||
|
Решение системы |
Значения выходных переменных |
Число итераций
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
1 |
1.0056 |
0.9874 |
0.9999 |
1.0036 |
0.9848 |
2 |
|
|||
|
2 |
1.9851 |
1.9765 |
1.9108 |
1.9629 |
1.9373 |
2 |
|
|||
В расчетах с помехой 5 % при увеличении параметра 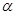 по некоторым координатам наблюдалось незначительное улучшение качества оценки.
по некоторым координатам наблюдалось незначительное улучшение качества оценки.
Помеха 5 %.
|
Объем обучающей выборки |
Решение системы |
Значения выходных переменных |
Число итераций
|
||||
|
|
|
|
|
|
|||
|
200 |
1 |
1.0242 |
1.0114 |
1.0074 |
1.0344 |
0.9967 |
8 |
|
2 |
2.006 |
2.0083 |
2.0308 |
2.0281 |
1.9736 |
8 |
|
|
400 |
1 |
0.9903 |
0.9837 |
1.0035 |
1.0107 |
0.9918 |
14 |
|
2 |
2.0076 |
2.0041 |
1.9904 |
2.0117 |
1.9884 |
14 |
|
С ростом объема обучающей выборки увеличивалось число итераций поиска при неизменных параметрах алгоритма, что было связано с численным уменьшением нормы невязок. Также при увеличении объема обучающей выборки наблюдалось небольшое уменьшение ошибки оценивания.
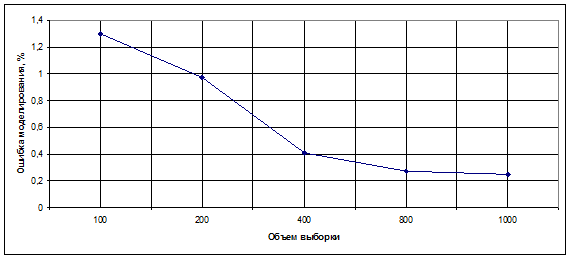
Рис 3. График сходимости оценки решения к истинному значению
Библиографический список
1. Красноштанов А.П. Комбинированные многосвязные системы. – Новосибирск: Наука, 2001. – 176с.
2. Медведев А.В. Непараметрические системы адаптации.– Новосибирск: Наука, 1983 – 173с.
3. Фельдбаум А.А. Основы теории оптимальных автоматических систем. Москва. Изд. Физматгиз, 1963г. - 552с.
4. Рубан А.И. Методы анализа данных: Учебное пособие. – Красноярск: ИПЦ КГТУ, 2004. – 319 с.







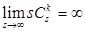 .
.