В этой работе метод вариационных итераций (МВИ) применяется для решения линейных и нелинейных обыкновенных дифференциальных уравнений. МВИ обеспечивает последовательность функций, которая сходится к точному решению и способен отменить некоторые из повторных вычислений. Метод очень прост и удобен.
Ключевые слова: дифференциальные уравнения, метод вариационных итераций, коррекция функционала, начальное приближение, последовательность функции, точное решение
В 1999 году метод вариационных итераций (МВИ) был предложен в работах J. H. Не [1,2]. Этот метод сейчас широко используется многими исследователями для изучения линейных и нелинейных обыкновенных дифференциальных уравнений и уравнений с частными производными. Метод представляет надежный и эффективный процесс для широкого спектра научных и инженерных приложений. Математические модели многих физических и механических процессов являются линейными или нелинейными, однородными или неоднородные, уравнения и системы уравнений. Решения таких уравнений методом вариационных итераций было показано многими авторами: J. H. Не, А. М. Wazwaz, Т. А. Abbasy, М. А. Abdou, Е. М. Abulwafa, S.Momani и др. [1–5], что этот метод более мощнее, чем существующие, такие как метод гомотопических возмущений, метод разложения Adomian, метод дифференциальных преобразований и др.
Метод дает быстро сходящиеся последовательные приближения к точному решению, если такое решение существует; в противном случае некоторые из этих приближений могут быть использованы для дальнейших численных целей. Существующие численные методики имеют ограниченные допущения, которые используются для обработки нелинейных членов, а МВИ не имеет каких-либо конкретных требований, таких как линеаризация, малые параметры, многочлены Adomian и т. д. для нелинейных операторов. Другим важным преимуществом является то, что метод вариационных итераций способен значительно уменьшая размер расчета при сохранении высокой точности численного решения. Кроме того, способность метода придает ему более широкое применение в обработке огромное количество аналитические и численные приложения. Значительный объем исследовательской работы было вложено в исследование линейных и нелинейных обыкновенных дифференциальных уравнений и уравнений с частными производными и их системы [5,6].
Целью данной работы является применить МВИ к решению линейных и нелинейных ОДУ с переменными коэффициентами из множества различных порядков, а также подтвердить надежность данного метода в обработке научных проблем.
Постановка задачи иалгоритм метода вариационных итераций. Рассмотрим дифференциальное уравнение
![]() , (1)
, (1)
где L и N — являются линейные и нелинейные операторы, соответственно; q(х) является источником, неоднородный член. Вариационный метод итераций допускает использование коррекции функционал для уравнения (1) в виде
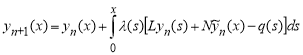 , (2)
, (2)
где — общий множитель Лагранжа, который может быть определены оптимальным образом с помощью вариационной теории и изменение ![]() ограничено, а это означает что
ограничено, а это означает что ![]() = 0. Множитель Лагранжа имеет решающее значение и критический в методе, и это может быть константой или функцией. Определяя , итерационная формула должна быть использована для определения самой последовательные приближения yn+1(х), n ≥ 0, которая приближается к решению y(x). Нулевое приближение y0 может быть выборочного функция. Тем не менее, с использованием начальных значений y(0), y′(0) и y′′(0) предпочтительно используем для выборочного нулевого приближения y0, как будет показано ниже. Следовательно, имеем решение
= 0. Множитель Лагранжа имеет решающее значение и критический в методе, и это может быть константой или функцией. Определяя , итерационная формула должна быть использована для определения самой последовательные приближения yn+1(х), n ≥ 0, которая приближается к решению y(x). Нулевое приближение y0 может быть выборочного функция. Тем не менее, с использованием начальных значений y(0), y′(0) и y′′(0) предпочтительно используем для выборочного нулевого приближения y0, как будет показано ниже. Следовательно, имеем решение
![]() (3)
(3)
Рассмотрим частные случаи:
1) ОДУ первого порядка. Пусть начальная задача имеет вид
![]() . (4)
. (4)
Для множителя Лагранжа установлены, что = –1. Коррекция функционала дает итерационную формулу
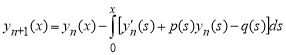 , n ≥ 0. (5)
, n ≥ 0. (5)
2) ОДУ второго порядка. Пусть начальная задача имеет вид
![]() . (6)
. (6)
Для множителя Лагранжа установлены, что = s — t. Коррекция функционала дает итерационную формулу
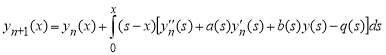 , n ≥ 0. (7)
, n ≥ 0. (7)
3) ОДУ m-го порядка. Пусть начальная задача имеет вид
![]() (8)
(8)
где m — порядок ОДУ. Множитель Лагранжа ![]() . Коррекция функционала дает итерационную формулу
. Коррекция функционала дает итерационную формулу
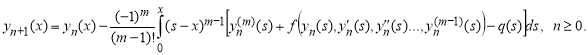 (9)
(9)
Хотя нулевое приближение y0(х) является любой выборочной функцией, но предпочтительно, чтобы выбрать его в виде
![]() . (10)
. (10)
Ниже приведены иллюстративные примеры. В них рассмотрены различные линейные и нелинейные неоднородные ОДУ разного порядка с переменными коэффициентами.
Пример 1. Рассмотрим следующую начальную задачу с неоднородным нелинейным ОДУ первого порядка
![]()
Для решения этой задачи применяем вышеописанную алгоритм МВИ для ОДУ первого порядка. Тогда для заданной задачи = –1 и начальное приближение равно y0(0) = 1. Соответствующая итерационная формула имеет вид
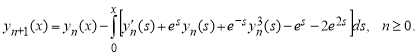
Исходя из этих, вынесем последующие приближения:
![]()
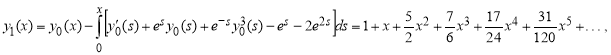
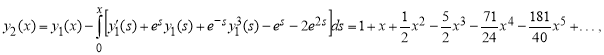
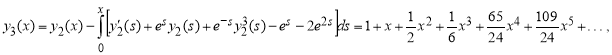
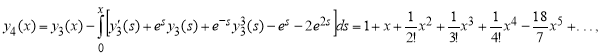
..., ![]()
Точное решение задачи имеет вид: ![]()
Пример 2. Рассмотрим следующую начальную задачу с неоднородным линейным ОДУ второго порядка с переменными коэффициентами
![]()
Для решения этой задачи применяем вышеописанную алгоритм МВИ для ОДУ второго порядка. Тогда для заданной задачи
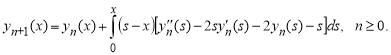
Исходя из этих, вынесем последующие приближения:
![]()
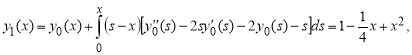
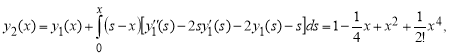
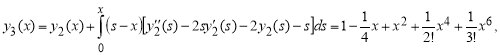 ...
...
![]()
Точное решение задачи имеет вид: ![]()
Пример 3. Рассмотрим следующую начальную задачу с неоднородным нелинейным ОДУ третьего порядка с переменными коэффициентами
![]()
Для решения этой задачи применяем вышеописанную алгоритм МВИ для ОДУ второго порядка. Тогда для заданной задачи
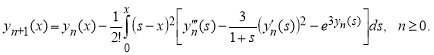
Исходя из этих, вынесем последующие приближения:
![]()
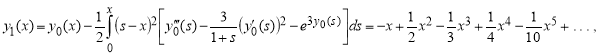
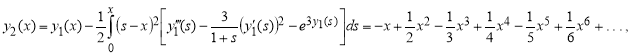
![]()
Точное решение задачи имеет вид: ![]()
Пример 4. Рассмотрим следующую начальную задачу с неоднородным нелинейным ОДУ четвертого порядка с переменными коэффициентами
![]()
Для решения этой задачи применяем вышеописанную алгоритм МВИ для ОДУ второго порядка. Тогда для заданной задачи ![]() и начальное приближение равно
и начальное приближение равно ![]() Соответствующая итерационная формула имеет вид
Соответствующая итерационная формула имеет вид
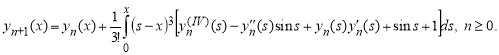
Исходя из этих, вынесем последующие приближения:
![]()
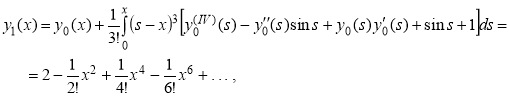
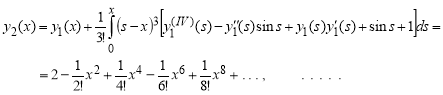
![]()
Точное решение задачи имеет вид: ![]()
Заключение. Результаты показывают, что МВИ является мощный математический инструмент для нахождения численных решений линейных и нелинейных обыкновенных дифференциальных уравнений. МВИ весьма эффективна для решения различных типов ОДУ разного порядка. В этой работе мы использовали метод вариационных итераций для решения начальных задач с линейными и нелинейными обыкновенными дифференциальными уравнениями. Этот приближенный метод широко распространены по приложениям. Этим приближенным методом можно эффективно, легко и точно решать большой класс нелинейных проблем, связанные с приближениями быстро сходящихся к точным решениям. Для нелинейных задач где точное решение не существует, небольшое число приближений могут быть использованы для численных целей. Таким образом, результаты исследований данной работы показало, что МВИ и можно распространить к нелинейным задачам математической физики.
Литература:
- He J. H. Variational iteration method for autonomous ordinary differential systems, Appl. math. Comput., 114(2/3), 2000, P.115–123.
- He J. H. Variational iteration method — Some recent results and new interpretations, J. Comput. Appl. Math., 207(1), 2007, P.3–17.
- Wazwaz A. M. The variational iteration method for analytic treatment for linear and nonlinear ODEs, Appl. Math. Comput., 212 (1), 2009, P.120–134.
- Wazwaz A. M. The variational iteration method for solving linear and nonlinear ODEs and scientific models with variable coefficients. Cent. Eur. J. Eng., 4(1), 2014, P.64–71.
- Wazwaz A. M. Partial Differential Equations and Solitary Waves Theory. Higher Education Press, Beijing and Springer-Verlag Berlin Heidelberg, 2009. — 761 p.
- Полянин А. Д., Зайцев В. Ф., Журов А. И. Методы решения нелинейных уравнений математической физики и механики. — М.: ФИЗМАТЛИТ, 2005. — 256 с.







