Ключевые слова: механизм, структура, кинематика, звено, подвижность, скорость, степень, сопряжений, бидифференциальный
Дифференциальный механизм с одной степенью подвижности описан в работе [1]. В настоящей статье приведем структуру и кинематику такого механизма с двумя степенями подвижности (рисунок, а). Вследствие подвижности центральных звеньев его можно рассматривать в следующих вариантах:
|
Вариант |
Звено 1 |
Звено 5 |
Звено 6 |
|
1 |
N1 |
N5 |
0 |
|
2 |
N2 |
0 |
N6 |
|
3 |
0 |
N5 |
N6 |
Вариант 1. Ведущие звенья ― 1 и 5 (см. рисунок а), количество пар V класса составляет [2]
P5=p5(1,0)+p5(2,1)+p5(3,2)+p5(4,1)+p5(5,0)=5,
IV класса―
P4=p4(5,2)+p4(4,3)+p4(6,4)=3,
Число подвижных звеньев―
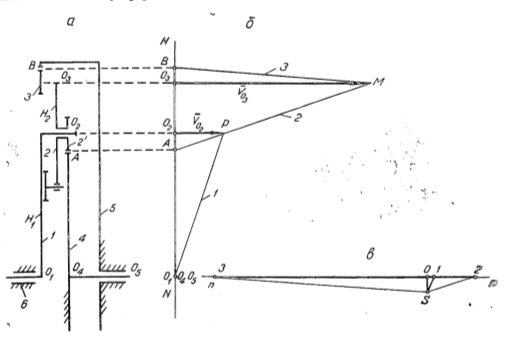
Кинематическая схема (а) и план линейных (б) и угловых (в) скоростей бидифференциального механизма.
n=n(1,0)+n(2,0)+n(3,0)+n(4,0)+n(5,0)=5
Степень подвижности находится по формуле П. Л. Чебышева [3,4]
W=3n-2p5–1p4 (1)
Подставляя значения n, p5 и p4 в структурную формулу (1), получаем W=2.
Рассмотрим кинематику дифференциального механизма (см. рисунок, а).
Линейные и угловые скорости характерных точек и звеньев механизма определяются графическим методом (рисунок, б, в).
Угловые скорости ω2, ω4 и ω3 (см. рисунок, а) можно вычислить аналитически с учетом векторных свойств радиусов сопряжения [5]:
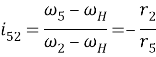
Учитывая, что ![]() , получаем
, получаем
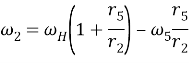 (2)
(2)
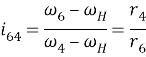
Отсюда
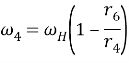 (3)
(3)
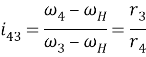
Принимая во внимание, что ![]() , имеем
, имеем
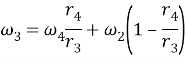 (4)
(4)
Подставляя выражения (2), и (3) в уравнение (4), записываем общую формулу для определения угловой скорости сателлита 3
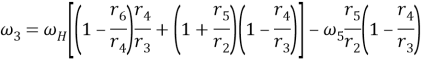 (5)
(5)
Вариант 2. Ведущие звенья―1 и 6. Выполняя операции по приведенной методике, получаем
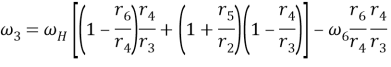 (6)
(6)
Вариант 3. Ведущие звенья―5 и 6. При этом имеем
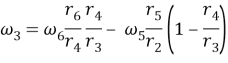 (7)
(7)
Литература^
- Файзиев И. Х., Кенжаев Р. Л. 1986. № 11. С. 15–16
- Файзиев И. Х., Джураева М. Ю. 1983. № 5. С. 10–11
- Артоболевский И. И. Теория механизмов. М.: Наука, 1965.
- Усманходжаев Х. Х. Теория механизмов и машин. На узб. Яз. Ташкент, 1981.
- Файзиев И. Х. 1969. № 1. С. 9–10.







